Como calcular sst, ssr e sse no excel

Freqüentemente usamos três somas de quadrados diferentes para medir quão bem uma linha de regressão realmente se ajusta a um conjunto de dados:

1. Soma dos Quadrados Totais (SST) – A soma dos quadrados das diferenças entre os pontos de dados individuais (y _i ) e a média da variável de resposta ( y ).

• SST = Σ(y _i – y ) ²

2. Regressão da Soma dos Quadrados (SSR) – A soma dos quadrados das diferenças entre os pontos de dados previstos (ŷ _i ) e a média da variável de resposta ( y ).

• SSR = Σ(ŷ _i – y ) ²

3. Erro da Soma dos Quadrados (SSE) – A soma dos quadrados das diferenças entre os pontos de dados previstos (ŷ _i ) e os pontos de dados observados (y _i ).

• SSE = Σ(ŷ _i – y _i ) ²

O exemplo passo a passo a seguir mostra como calcular cada uma dessas métricas para um determinado modelo de regressão no Excel.

Etapa 1: crie os dados

Primeiro, vamos criar um conjunto de dados contendo o número de horas estudadas e as notas dos exames obtidas para 20 alunos diferentes em uma determinada escola:

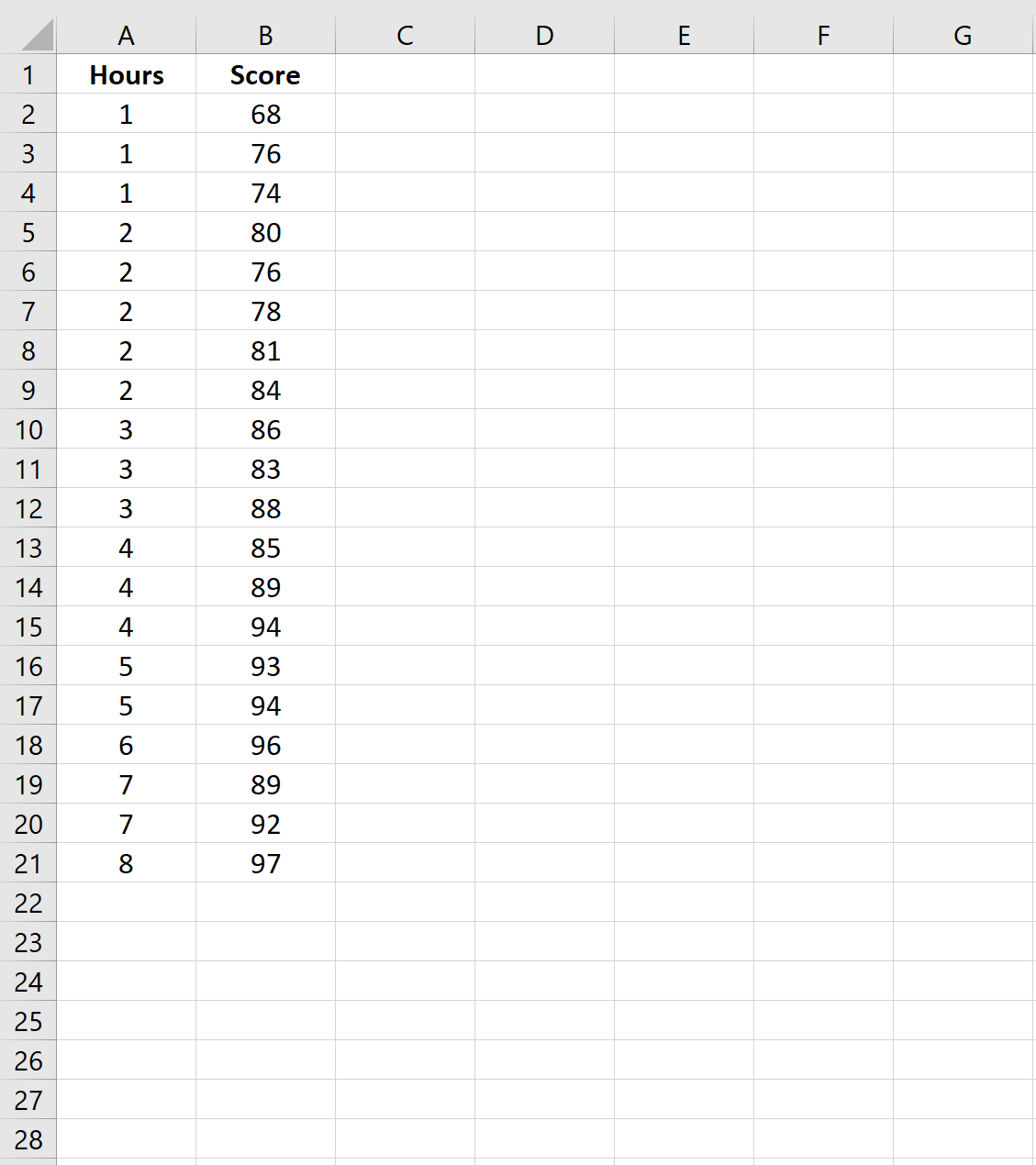
Passo 2: Ajustar um modelo de regressão

Na faixa superior do Excel, clique na guia Dados e clique em Análise de Dados . Se você não vir essa opção, primeiro instale o software Analysis ToolPak gratuito .

Depois de clicar em Análise de Dados, uma nova janela aparecerá. Selecione Regressão e clique em OK.

Na nova janela que aparece, forneça as seguintes informações:

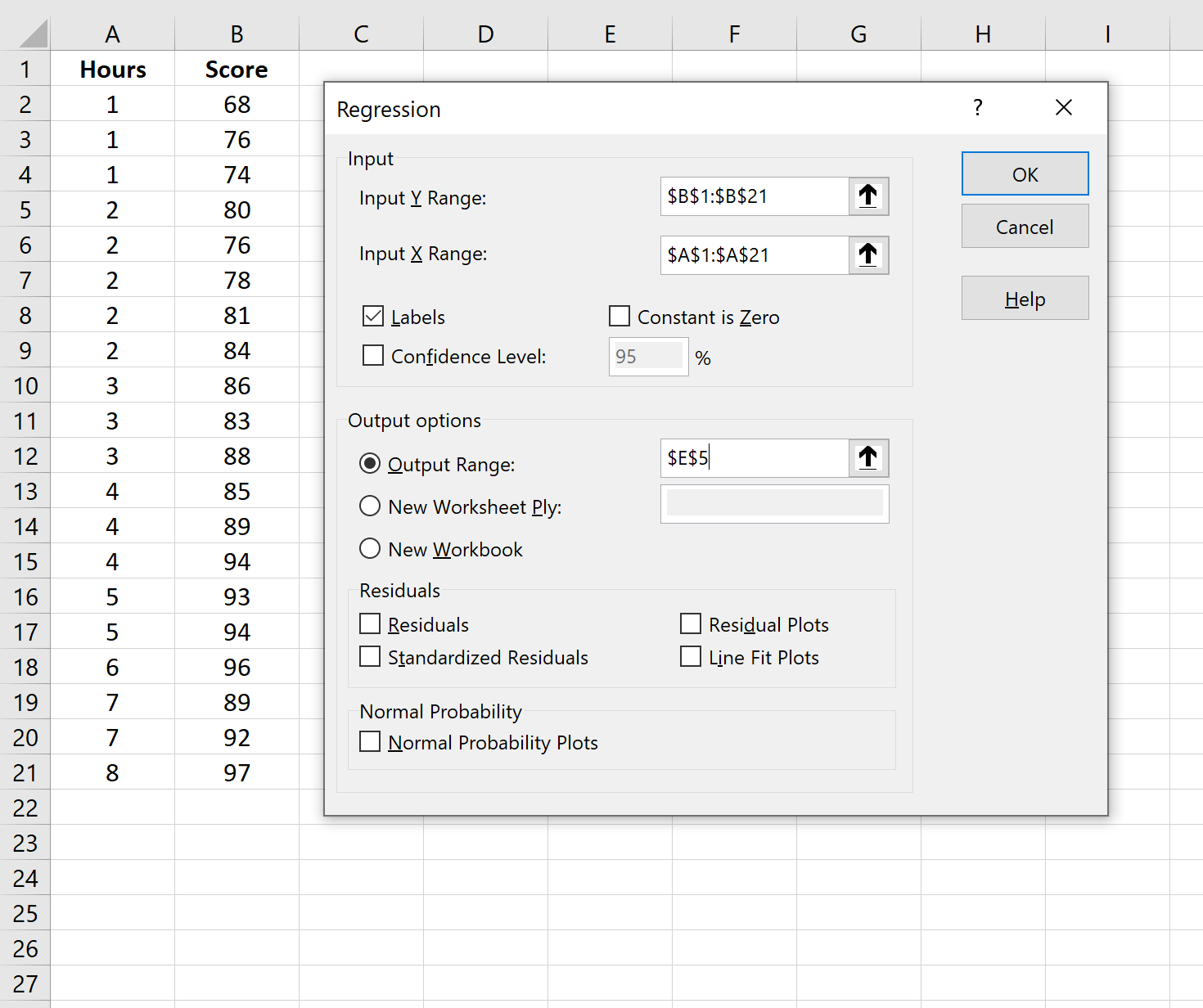
Depois de clicar em OK , a saída da regressão aparecerá.

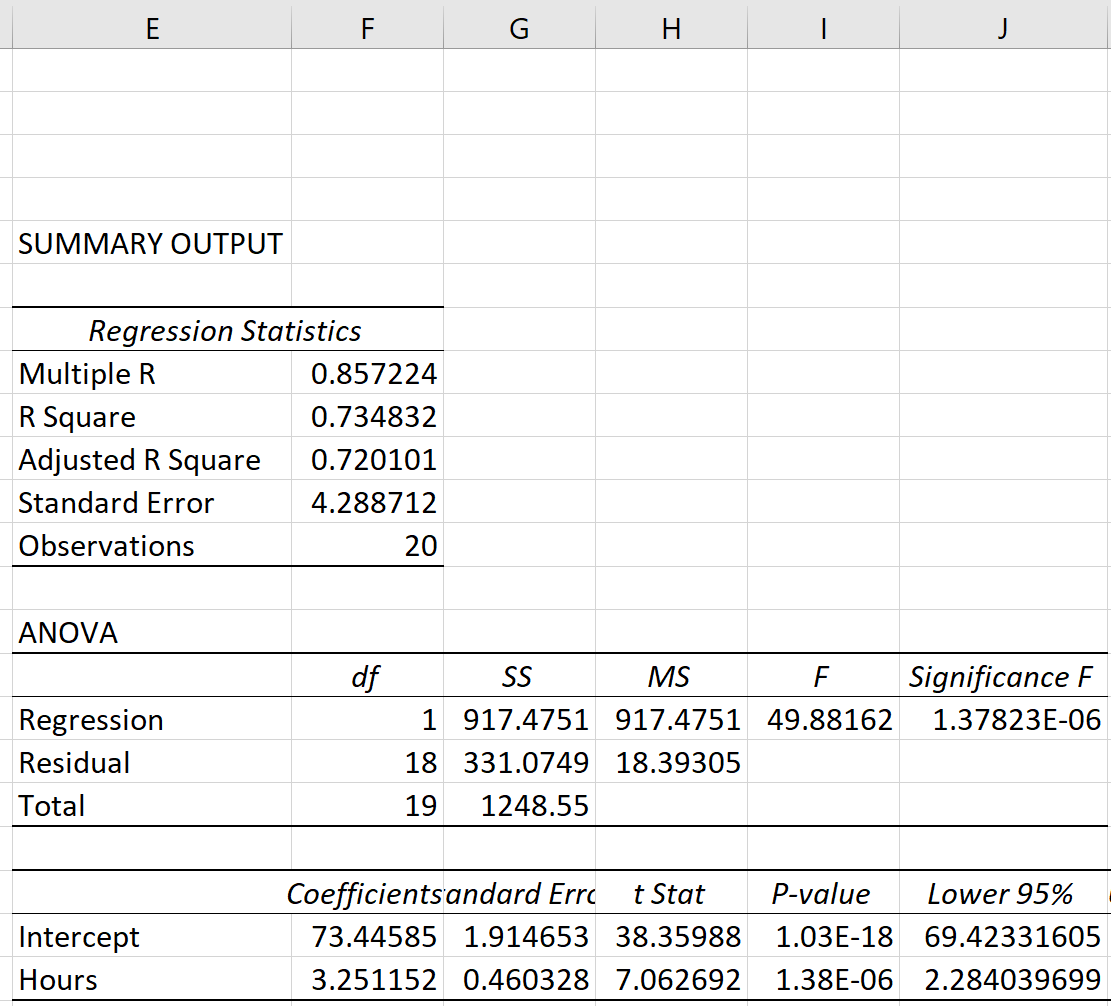
Etapa 3: analise o resultado

As três métricas de soma de quadrados – SST, SSR e SSE – podem ser vistas na coluna SS da tabela ANOVA :

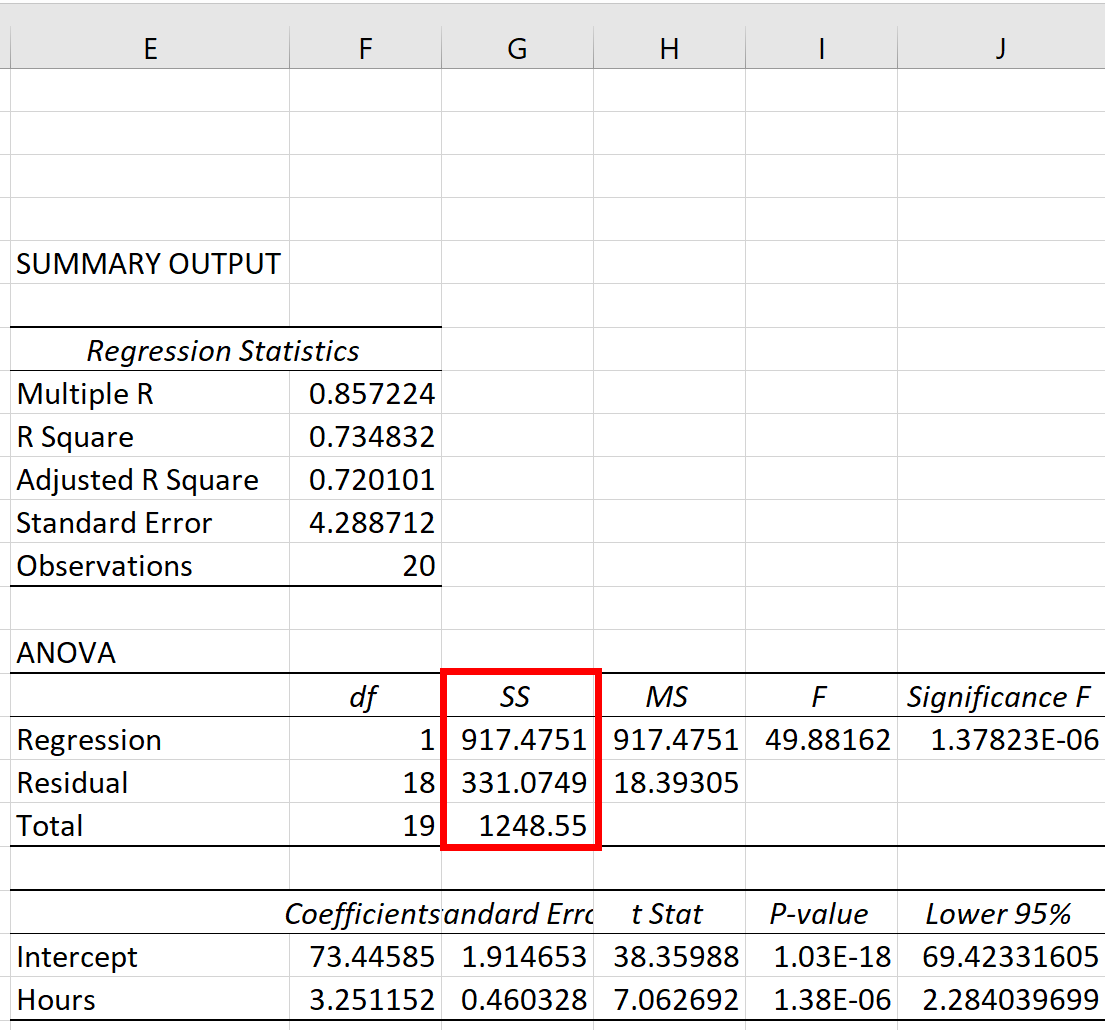
As métricas acabam sendo:

• Soma total dos quadrados (SST): 1248,55
• Regressão da Soma dos Quadrados (SSR): 917,4751
• Erro da soma dos quadrados (SSE): 331,0749

Podemos verificar que SST = SSR + SSE:

• SST = SSR + SSE
• 1248,55 = 917,4751 + 331,0749

Também podemos calcular manualmente o R ao quadrado do modelo de regressão:

• R ao quadrado = SSR / SST
• R ao quadrado = 917,4751/1248,55
• R ao quadrado = 0,7348

Isso nos diz que 73,48% da variação nas notas dos exames pode ser explicada pela quantidade de horas estudadas.

Recursos adicionais

Como realizar regressão linear simples no Excel
Como realizar regressão linear múltipla no Excel
Como realizar regressão polinomial no Excel
Como realizar regressão exponencial no Excel