O que é y hat nas estatísticas?

Em estatística, o termo y hat (escrito ŷ ) refere-se ao valor estimado de uma variável resposta em um modelo de regressão linear .

Geralmente escrevemos uma equação de regressão estimada da seguinte forma:

ŷ = β ₀ + β ₁ x

Ouro:

• ŷ : O valor estimado da variável resposta
• β ₀ : O valor médio da variável de resposta quando a variável preditora é zero
• β ₁ : variação média na variável resposta associada ao aumento de uma unidade na variável preditiva

Por exemplo, suponha que temos o seguinte conjunto de dados que mostra o número de horas estudadas por seis alunos diferentes, juntamente com as notas dos exames finais:

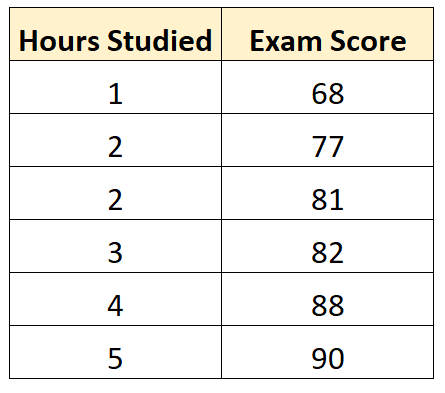
Suponha que usamos software estatístico (como R , Excel , Python ou mesmo manualmente) para ajustar o seguinte modelo de regressão usando horas estudadas como variável preditora e examinar os resultados como variável resposta:

Pontuação = 66,615 + 5,0769*(Horas)

A forma de interpretar os coeficientes de regressão neste modelo é a seguinte:

• A nota média do exame para um aluno que estuda zero horas é 66.615 .
• A nota do exame aumenta em média 5,0769 pontos para cada hora adicional estudada.

Podemos usar esta equação de regressão para estimar a pontuação de um determinado aluno com base no número de horas estudadas.

Por exemplo, um aluno que estuda 3 horas deve obter uma pontuação de:

Pontuação = 66,615 + 5,0769*(3) = 81,85

Por que o chapéu Y é usado?

O símbolo “chapéu” nas estatísticas é usado para denotar qualquer termo “estimado”. Por exemplo, ŷ é usado para denotar uma variável de resposta estimada.

Normalmente, quando ajustamos modelos de regressão linear, usamos uma amostra de dados de uma população, porque isso é mais conveniente e consome menos tempo do que coletar dados para cada observação possível em uma população.

Portanto, quando encontramos uma equação de regressão, estamos apenas estimando a verdadeira relação entre uma variável preditora e uma variável de resposta.

É por isso que usamos o termo ŷ na equação de regressão em vez de y.

Recursos adicionais

Introdução à regressão linear simples
Introdução à regressão linear múltipla
Introdução às variáveis explicativas e de resposta