Uma introdução à distribuição uniforme

A distribuição uniforme é uma distribuição de probabilidade em que cada valor entre um intervalo de a a b tem a mesma probabilidade de ocorrer.

Se uma variável aleatória X segue uma distribuição uniforme, então a probabilidade de X assumir um valor entre x ₁ e x ₂ pode ser encontrada pela seguinte fórmula:

P(x ₁ < X < x ₂ ) = (x ₂ – x ₁ ) / (b – a)

Ouro:

• x ₁ : o menor valor de juros
• x ₂ : o valor superior de interesse
• a: o valor mínimo possível
• b: o valor máximo possível

Por exemplo, suponha que o peso dos golfinhos esteja distribuído uniformemente entre 100 e 150 libras.

Se selecionarmos um golfinho aleatoriamente, podemos usar a fórmula acima para determinar a probabilidade de o golfinho escolhido pesar entre 120 e 130 libras:

• P(120 < X < 130) = (130 – 120) / (150 – 100)
• P(120 < X < 130) = 10/50
• P(120 < X < 130) = 0,2

A probabilidade de o golfinho escolhido pesar entre 120 e 130 libras é de 0,2 .

Visualize distribuição uniforme

Se criarmos um gráfico de densidade para visualizar a distribuição uniforme, ele se parecerá com o seguinte gráfico:

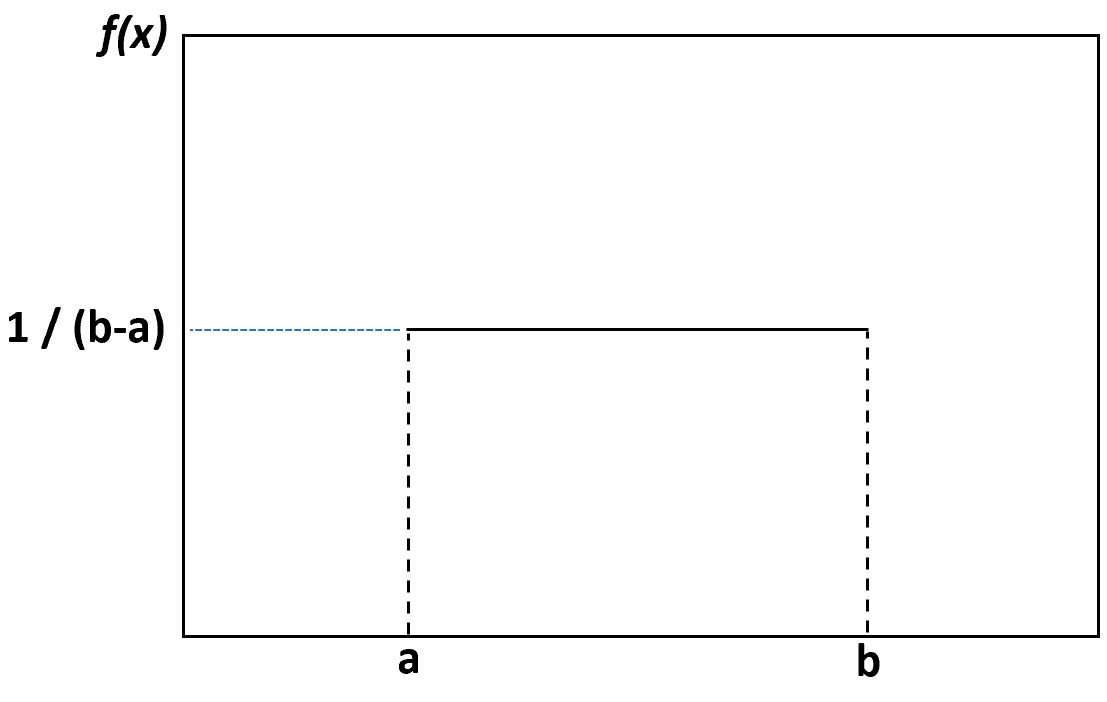
Todo valor entre o limite inferior a e o limite superior b tem a mesma probabilidade de ocorrer e qualquer valor fora desses limites tem probabilidade zero.

Por exemplo, no nosso exemplo anterior, dissemos que o peso dos golfinhos está distribuído uniformemente entre 100 e 150 libras. Veja como visualizar essa distribuição:

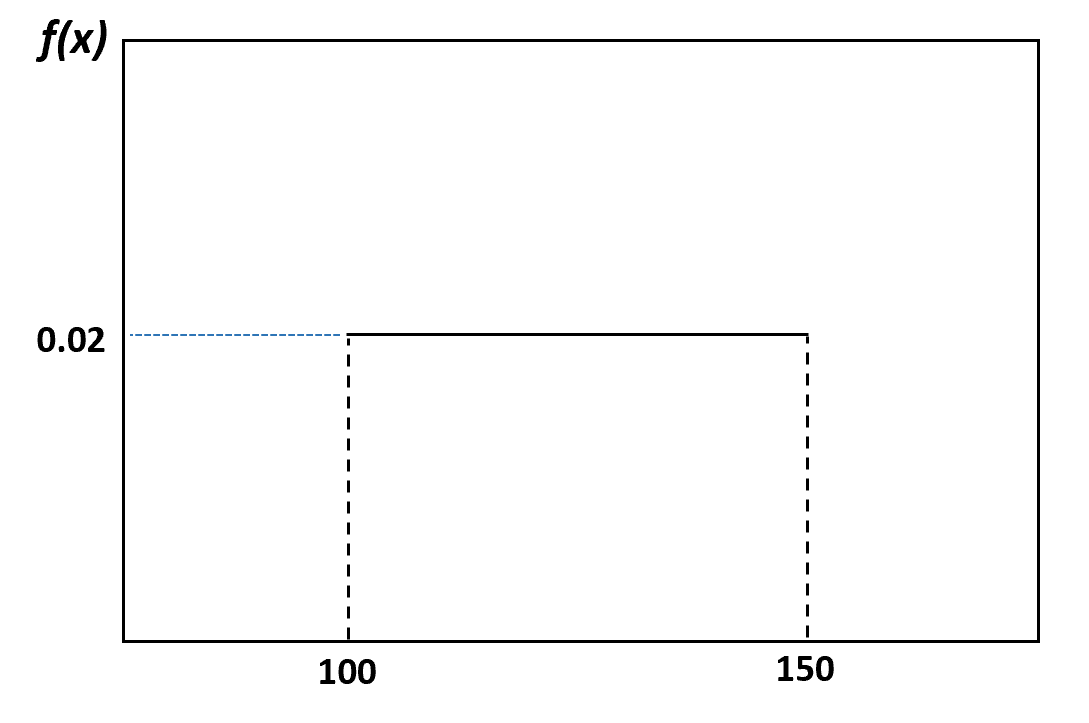
E a probabilidade de um golfinho selecionado aleatoriamente pesar entre 120 e 130 libras pode ser visualizada da seguinte forma:

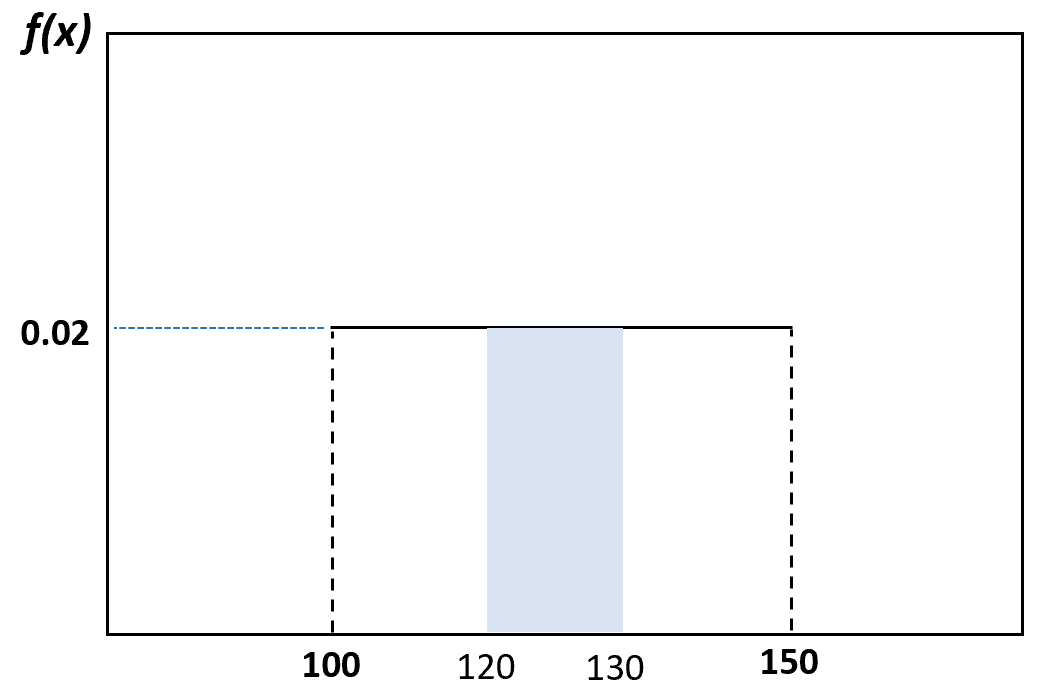
Propriedades de distribuição uniforme

A distribuição uniforme tem as seguintes propriedades:

• Média: (a + b) / 2
• Mediana: (a + b) / 2
• Desvio padrão: √ (b – a) ^2/12
• Diferença: (b – a) ^2/12

Por exemplo, suponha que o peso dos golfinhos esteja distribuído uniformemente entre 100 e 150 libras.

Poderíamos calcular as seguintes propriedades para esta distribuição:

• Peso médio: (a + b) / 2 = (150 + 100) / 2 = 125
• Peso mediano: (a + b) / 2 = (150 + 100) / 2 = 125
• Desvio padrão do peso: √ (150 – 100) ^2/12 = 14,43
• Variação de peso: (150 – 100) ^2/12 = 208,33

Problemas com práticas de distribuição uniformes

Use os seguintes problemas práticos para testar seu conhecimento sobre distribuição uniforme.

Questão 1: Um ônibus chega a um ponto de ônibus a cada 20 minutos. Se você chegar ao ponto de ônibus, qual é a probabilidade de o ônibus chegar em 8 minutos ou menos?

Solução 1: O tempo mínimo de espera é 0 minutos e o tempo máximo de espera é 20 minutos. O valor de juros inferior é 0 minutos e o valor de juros superior é 8 minutos.

Então, calcularíamos a probabilidade da seguinte forma:

P(0 < X < 8) = (8-0) / (20-0) = 8/20 = 0,4 .

Questão 2: A duração de um jogo da NBA é distribuída uniformemente entre 120 e 170 minutos. Qual é a probabilidade de um jogo da NBA selecionado aleatoriamente durar mais de 155 minutos?

Solução 2: A duração mínima é de 120 minutos e a duração máxima é de 170 minutos. O valor de juros inferior é de 155 minutos e o valor de juros superior é de 170 minutos.

Então, calcularíamos a probabilidade da seguinte forma:

P(155 < X < 170) = (170-155) / (170-120) = 15/50 = 0,3 .

Questão 3: O peso de uma determinada espécie de rã está distribuído uniformemente entre 15 e 25 gramas. Se você selecionar um sapo ao acaso, qual é a probabilidade de ele pesar entre 17 e 19 gramas?

Solução 3: O peso mínimo é 15 gramas e o peso máximo é 25 gramas. O valor de juros inferior é de 17 gramas e o valor de juros superior é de 19 gramas.

Então, calcularíamos a probabilidade da seguinte forma:

P(17 < X < 19) = (19-17) / (25-15) = 2/10 = 0,2 .

Nota: Podemos usar a Calculadora de Distribuição Uniforme para verificar nossas respostas para cada um desses problemas.