Tipos médios (estatísticas)

By Dr. benjamim anderson Agosto 6, 2023 Estatisticas 0 Comments

Aqui explicamos o que são todos os tipos de médias nas estatísticas e como são calculadas. Você encontrará a fórmula para cada tipo de meia e exemplos.

Mas antes de ver quais são os tipos de média, devemos saber logicamente o que é uma média nas estatísticas. Portanto, recomendamos que você consulte o seguinte link antes de continuar.

➤ Veja: Qual é a média (estatísticas)?

Quais são os tipos de médias nas estatísticas?

Nas estatísticas, os tipos de médias são:

Média aritmética
Média ponderada
Meios geométricos
raiz significa quadrado
significado harmônico
média generalizada
média f generalizada
meios aparados
média interquartil
média de uma função

A seguir explicaremos como calcular todos os tipos de médias nas estatísticas. Os cinco tipos de média mais comumente usados são média aritmética, média ponderada, média geométrica, média quadrática e média harmônica. Então, entraremos em mais detalhes sobre esses cinco principais tipos de mídia.

Média aritmética

A média aritmética é calculada somando todos os valores e depois dividindo pelo número total de pontos de dados.

A fórmula para a média aritmética é, portanto, a seguinte:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+\dots+x_N}{N}$

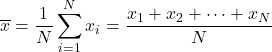
A média aritmética também é conhecida como média aritmética .

A média aritmética é provavelmente o tipo de média mais utilizado nas estatísticas.

Para ver um exemplo de como esse tipo de média é obtido, calcularemos a média aritmética dos seguintes dados:

$4\quad 7\quad 10\quad 1\quad 8\quad9$

Para calcular a média aritmética, basta somar todos os dados estatísticos e dividir pelo número total de dados, que é 6:

$\overline{x}=\cfrac{4+7+10+1+8+9}{6}=6,5$

Média ponderada

Para calcular a média ponderada, você deve primeiro multiplicar cada dado estatístico pelo seu peso (ou peso), depois somar todos os produtos e, por fim, dividir a soma ponderada pela soma de todos os pesos.

A fórmula da média ponderada é, portanto, a seguinte:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+\dots x_N\cdot w_N}{w_1+w_2+\dosts +w_N}$

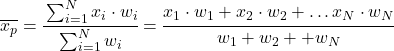
Onde x _i é o valor estatístico e w _i o peso correspondente.

A média ponderada é mais difícil de entender, por isso recomendamos conferir o exemplo a seguir que explica passo a passo como ela é calculada:

➤ Veja: Exemplo de média ponderada

Meios geométricos

A média geométrica de um conjunto de dados estatísticos é igual à enésima raiz do produto de todos os valores.

Esse tipo de média é usado em finanças empresariais para calcular taxas de retorno, médias percentuais e juros compostos.

A fórmula para este tipo de armazenamento é bastante complicada. Na verdade, a média geométrica de todos os conjuntos estatísticos não pode ser calculada, mas por vezes este tipo de média não pode ser determinado. É por isso que recomendamos que você consulte todas as exceções explicadas no seguinte link:

➤ Veja: fórmula da média geométrica

raiz significa quadrado

A raiz quadrada média é igual à raiz quadrada da média aritmética dos quadrados dos dados.

A fórmula quadrática média é, portanto, a seguinte:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

Esse tipo de média também é chamado de raiz quadrada média , raiz quadrada média ou RMS .

Ressaltamos apenas que a média cúbica também existe, mas é utilizada em casos muito especiais.

A média quadrada tem vantagens e desvantagens, por exemplo, é particularmente útil quando a variável estatística assume valores positivos e negativos, porque ao elevar ao quadrado cada dado, todos os valores se tornam positivos. Você pode ver mais recursos deste tipo de mídia clicando no link a seguir:

➤ Veja: vantagens e desvantagens da raiz quadrada média

significado harmônico

A média harmônica é calculada dividindo o número total de dados estatísticos pela soma dos recíprocos de cada valor.

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}$

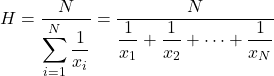
A média harmônica é usada para calcular velocidades médias, tempos ou fazer cálculos eletrônicos. Essa característica diferencia a média harmônica de outros tipos de médias, frequentemente utilizadas no cálculo de médias de preços ou percentuais.

Você pode ver exemplos de cálculo deste tipo de média na página seguinte:

➤ Veja: exemplos de significado harmônico

Outros tipos de meias

Nesta seção veremos as fórmulas para outros tipos de meias. Não entraremos em detalhes sobre cada tipo porque elas não são muito utilizadas, mas é bom que você saiba que existem outros tipos de meias.

A média generalizada é uma mistura dos tipos de média vistos acima e é calculada usando a seguinte fórmula:

$\displaystyle\overline{x}(m) = \left ( \frac{1}{N}\cdot\sum_{i=1}^N{x_i^m} \right ) ^{1/m}$

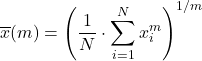
Seja f uma função injetiva e monotônica, então a f-média generalizada definida como:

$\displaystyle\overline{x} = f^{-1}\left({\frac{1}{N}\cdot\sum_{i=1}^N{f(x_i)}}\right)$

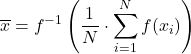
A média aparada envolve o cálculo da média aritmética após subtrair uma porcentagem de observações nas extremidades superior e inferior da amostra. A mesma percentagem deve ser rejeitada em ambos os extremos.

Para calcular a média interquartil , também chamada de média interquartil, primeiro são descartados os dados do primeiro e quarto quartis, e depois é calculada apenas a média aritmética do segundo e terceiro quartis da amostra. A fórmula para este tipo de média é, portanto:

$\displaystyle\overline{x}={2 \over n} \sum_{i=\frac{n}{4}+1}^{\frac{3n}{4}}{x_i}$

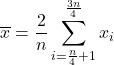
Finalmente, você também pode encontrar a média de uma função . O valor médio de uma função contínua em um intervalo fechado [a,b] é calculado usando a seguinte fórmula:

$\displaystyle\overline{f}=\frac{1}{b-a} \int_a^b f(t) dt$

Amostra e média populacional

Por fim, veremos qual é a diferença entre a média amostral e a média populacional, dois tipos de médias muitas vezes confundidas.

A média amostral é a média calculada sobre os valores de uma amostra estatística, ou seja, é calculada sobre parte de todos os valores de uma variável.

A média populacional é a média calculada sobre uma população estatística, ou seja, sobre todos os valores de uma variável. Portanto, a média populacional coincide com a expectativa matemática da variável.

A média amostral pode ser considerada praticamente igual à média populacional se uma quantidade suficientemente grande de dados for conhecida. Mas o valor da média populacional é muito difícil de obter, pois na realidade todos os valores de uma distribuição raramente são conhecidos.

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais