Razão de chances ajustada: definição + exemplos

Nas estatísticas, uma razão de chances nos diz a razão entre a probabilidade de um evento ocorrer em um grupo de tratamento e a probabilidade de um evento ocorrer em um grupo de controle.

As razões de probabilidade aparecem mais comumente na regressão logística , que é um método que usamos para ajustar um modelo de regressão que possui uma ou mais variáveis preditoras e uma variável de resposta binária.

Um odds ratio ajustado é um odds ratio que foi ajustado para outras variáveis preditoras em um modelo.

É particularmente útil para nos ajudar a compreender como uma variável preditora afeta as chances de ocorrência de um evento, após ajuste para o efeito de outras variáveis preditoras.

O exemplo a seguir ilustra a diferença entre um odds ratio e um odds ratio ajustado.

Exemplo: Cálculo de odds ratios ajustados

Suponhamos que queremos entender se a idade da mãe afeta a probabilidade de ter um bebê com baixo peso ao nascer.

Para explorar isso, podemos realizar regressão logística usando a idade como variável preditora e o baixo peso ao nascer (sim ou não) como variável resposta .

Suponha que coletamos dados de 300 mães e ajustamos um modelo de regressão logística. Aqui estão os resultados:

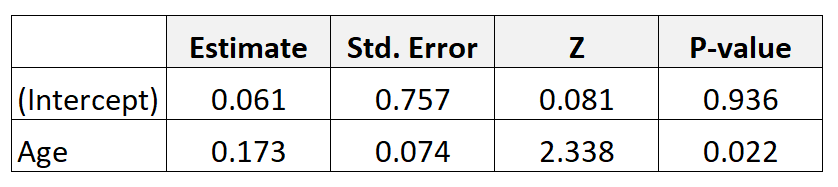
Para obter a razão de chances para idade, basta exponenciar a estimativa do coeficiente da tabela: e ^0,173 = 1,189 .

Isto diz-nos que um aumento de um ano na idade está associado a um aumento de 1.189% nas probabilidades de um bebé ter baixo peso à nascença. Ou seja, as chances de ter um bebê com baixo peso ao nascer aumentam 18,9% para cada aumento anual adicional de idade.

Este odds ratio é chamado de odds ratio “bruto” ou odds ratio “não ajustado” porque não foi ajustado para as outras variáveis preditoras no modelo, uma vez que é a única variável preditora no modelo.

Mas suponhamos que queremos compreender se a idade da mãe e os hábitos de fumar afectam a probabilidade de ter um bebé com baixo peso à nascença.

Para explorar isso, podemos realizar regressão logística usando idade e tabagismo (sim ou não) como variáveis preditoras e baixo peso ao nascer como variável resposta .

Suponha que coletamos dados de 300 mães e ajustamos um modelo de regressão logística. Aqui estão os resultados:

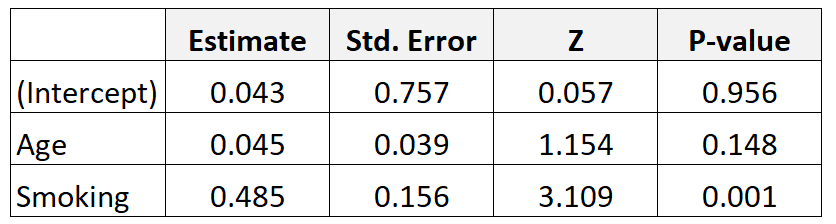
Veja como interpretar os resultados:

Idade: A razão de chances ajustada por idade é calculada da seguinte forma: e ^0,045 = 1,046 . Isto significa que as chances de ter um bebê com baixo peso ao nascer aumentam 4,6% para cada aumento anual adicional de idade, assumindo que a variável tabagismo permaneça constante.

Por exemplo, suponha que a Mãe A e a Mãe B fumem. Se a mãe A for um ano mais velha que a mãe B, então a probabilidade de a mãe A ter um bebê com baixo peso ao nascer é 1,046 vezes a probabilidade de a mãe B ter um bebê com baixo peso ao nascer.

Tabagismo : A razão de chances ajustada para fumar é calculada da seguinte forma: ^e,485 = 1,624 . Isso significa que as chances de ter um bebê com baixo peso ao nascer aumentam em 62,4% se a mãe fumar (em comparação a não fumar), supondo que a variável idade permaneça constante.

Por exemplo, suponha que a Mãe A e a Mãe B tenham ambas 30 anos. Se a mãe A fuma durante a gravidez e a mãe B não fuma, então as chances da mãe A ter um bebê com baixo peso ao nascer são 62,4% maiores do que as chances da mãe B ter um bebê com baixo peso ao nascer.

Observe que a razão de chances ajustada por idade é inferior à razão de chances não ajustada do exemplo anterior. Isso ocorre porque quando outras variáveis preditoras aumentam as chances de ocorrência da variável resposta, a razão de chances ajustada para uma variável preditora já presente no modelo sempre diminuirá.

Resumo: odds ratio versus odds ratio ajustado

Um odds ratio (às vezes chamado de odds ratio “bruto”) é útil para nos dizer como as mudanças em uma variável preditora afetam as chances de ocorrência de uma variável de resposta.

Um odds ratio ajustado é útil para nos dizer como as mudanças em uma variável preditora afetam as chances de ocorrência de uma variável de resposta, após controlar outras variáveis preditoras em um modelo.

Recursos adicionais

Introdução à regressão logística
Como realizar regressão logística em R
Como realizar regressão logística em Python