Binomial negativo vs poisson: como escolher um modelo de regressão

A regressão binomial negativa e a regressão de Poisson são dois tipos de modelos de regressão que devem ser usados quando a variável de resposta é representada por resultados de contagem discreta.

Aqui estão alguns exemplos de variáveis de resposta que representam resultados de contagem discretos:

• O número de alunos que se formam em um determinado programa
• O número de acidentes rodoviários em um determinado cruzamento
• O número de participantes que completam uma maratona
• O número de devoluções em um determinado mês em uma loja de varejo

Se a variância for aproximadamente igual à média, então um modelo de regressão de Poisson geralmente se ajusta bem a um conjunto de dados.

No entanto, se a variância for significativamente maior que a média, um modelo de regressão binomial negativo geralmente é capaz de ajustar melhor os dados.

Existem duas técnicas que podemos usar para determinar se a regressão de Poisson ou a regressão binomial negativa é mais apropriada para um determinado conjunto de dados:

1. Parcelas residuais

Podemos criar um gráfico dos resíduos padronizados em relação aos valores previstos de um modelo de regressão.

Se a maioria dos resíduos padronizados estiver entre -2 e 2, um modelo de regressão de Poisson é provavelmente apropriado.

No entanto, se muitos resíduos ficarem fora deste intervalo, um modelo de regressão binomial negativo provavelmente proporcionará um melhor ajuste.

2. Teste de razão de verossimilhança

Podemos ajustar um modelo de regressão de Poisson e um modelo de regressão binomial negativa ao mesmo conjunto de dados e então realizar um teste de razão de verossimilhança.

Se o valor p do teste estiver abaixo de um certo nível de significância (por exemplo, 0,05), então podemos concluir que o modelo de regressão binomial negativa proporciona um ajuste significativamente melhor.

O exemplo a seguir mostra como usar essas duas técnicas em R para determinar se é melhor usar uma regressão de Poisson ou um modelo de regressão binomial negativa para um determinado conjunto de dados.

Exemplo: regressão binomial negativa vs regressão de Poisson

Suponha que queiramos saber quantas bolsas um jogador de beisebol do ensino médio em um determinado condado recebe com base em sua divisão escolar (“A”, “B” ou “C”) e sua série escolar. vestibular (medido de 0 a 100). ).

Use as etapas a seguir para determinar se um modelo de regressão binomial negativa ou um modelo de regressão de Poisson fornece um melhor ajuste aos dados.

Etapa 1: crie os dados

O código a seguir cria o conjunto de dados com o qual trabalharemos, que inclui dados de 1.000 jogadores de beisebol:

 #make this example reproducible
set. seeds (1)

#create dataset
data <- data. frame (offers = c(rep(0, 700), rep(1, 100), rep(2, 100),
                              rep(3, 70), rep(4, 30)),
                   division = sample(c(' A ', ' B ', ' C '), 100, replace = TRUE ),
                   exam = c(runif(700, 60, 90), runif(100, 65, 95),
                            runif(200, 75, 95)))

#view first six rows of dataset
head(data)

  offers division exam
1 0 A 66.22635
2 0 C 66.85974
3 0 A 77.87136
4 0 B 77.24617
5 0 A 62.31193
6 0 C 61.06622

Etapa 2: Ajustar um modelo de regressão de Poisson e um modelo de regressão binomial negativo

O código a seguir mostra como ajustar um modelo de regressão de Poisson e um modelo de regressão binomial negativa aos dados:

 #fit Poisson regression model
p_model <- glm(offers ~ division + exam, family = ' fish ', data = data)

#fit negative binomial regression model
library (MASS)

nb_model <- glm. nb (offers ~ division + exam, data = data)

Etapa 3: criar gráficos residuais

O código a seguir mostra como produzir gráficos residuais para ambos os modelos.

 #Residual plot for Poisson regression
p_res <- resid (p_model)
plot(fitted(p_model), p_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Poisson ')
abline(0,0)

#Residual plot for negative binomial regression
nb_res <- resid (nb_model)
plot(fitted(nb_model), nb_res, col=' steelblue ', pch=16,
     xlab=' Predicted Offers ', ylab=' Standardized Residuals ', main=' Negative Binomial ')
abline(0,0) 

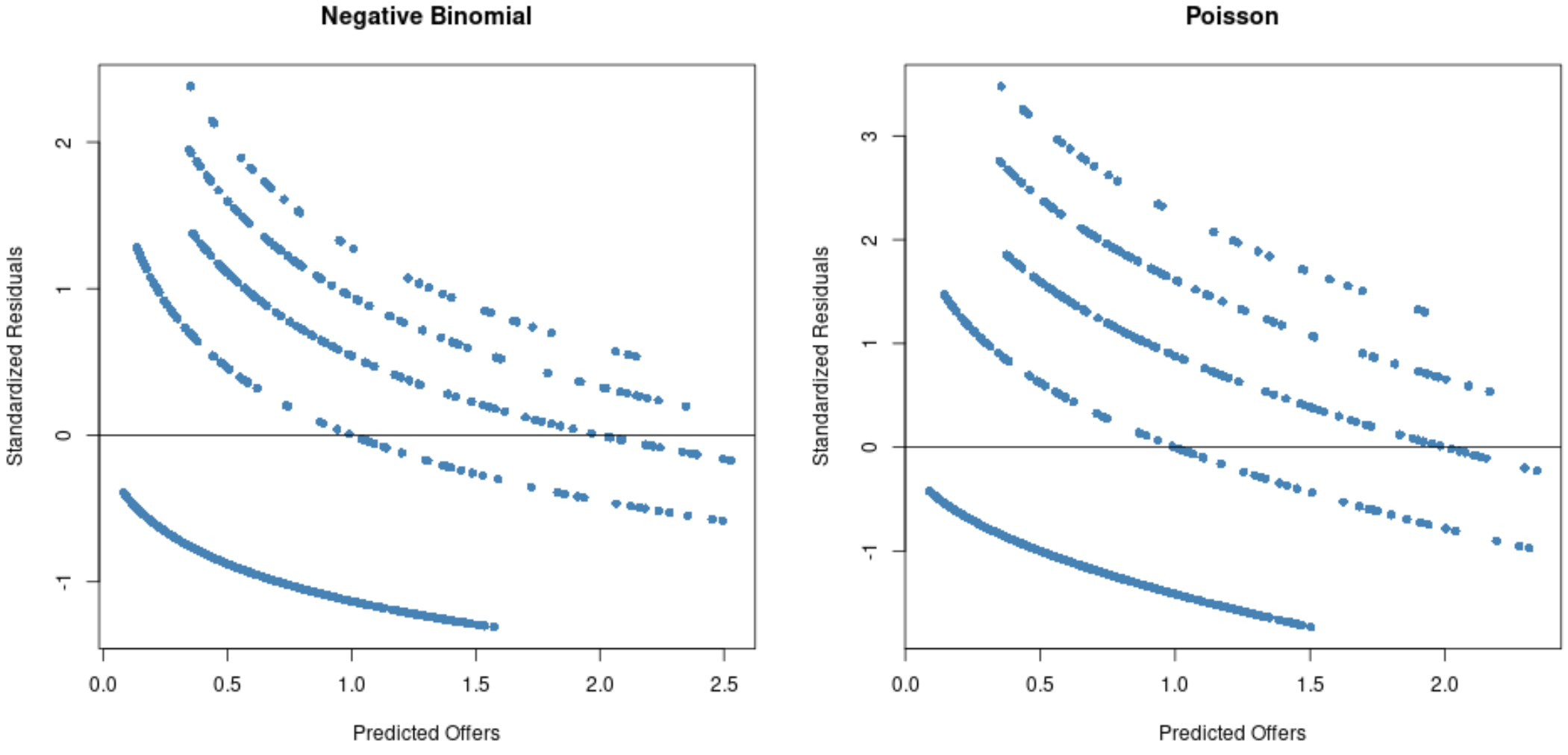
A partir dos gráficos, podemos ver que os resíduos estão mais espalhados para o modelo de regressão de Poisson (observe que alguns resíduos se estendem além de 3) em comparação com o modelo de regressão binomial negativa.

Isto é um sinal de que um modelo de regressão binomial negativa é provavelmente mais apropriado, uma vez que os resíduos deste modelo são menores.

Etapa 4: realizar um teste de razão de verossimilhança

Finalmente, podemos realizar um teste de razão de verossimilhança para determinar se há uma diferença estatisticamente significativa no ajuste dos dois modelos de regressão:

 pchisq(2 * ( logLik (nb_model) - logLik (p_model)), df = 1, lower. tail = FALSE )

'log Lik.' 3.508072e-29 (df=5)

O valor p do teste acabou sendo 3,508072e-29 , que é significativamente menor que 0,05.

Assim, concluiríamos que o modelo de regressão binomial negativa proporciona um ajuste significativamente melhor aos dados em comparação com o modelo de regressão de Poisson.

Recursos adicionais

Uma introdução à distribuição binomial negativa
Uma introdução à distribuição de Poisson