Frequência relativa
Neste artigo você aprenderá o que é frequência relativa em estatísticas, como obter frequência relativa e dois exercícios passo a passo resolvidos sobre frequência relativa.
O que é frequência relativa?
Nas estatísticas, a frequência relativa é uma medida que indica o número de vezes que um valor aparece em uma amostra de dados como uma proporção ou porcentagem. Mais precisamente, a frequência relativa é igual à frequência absoluta dividida pelo número total de dados.
Por exemplo, se a frequência absoluta de um valor for 15 e houver 100 pontos de dados no total, a frequência relativa desse valor será 0,15 (15/100=0,15).
Geralmente, o símbolo h i é usado para representar a frequência relativa. Embora ainda não haja consenso na comunidade estatística, você pode ver a frequência relativa representada por outro símbolo.
Como calcular a frequência relativa
A frequência relativa é igual à frequência absoluta dividida pelo número total de dados. Portanto, para calcular a frequência relativa, você deve primeiro encontrar a frequência absoluta e depois dividi-la pelo número total de observações.
Portanto, a fórmula da frequência relativa é a seguinte:
![]()
Ouro:
-
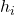
é a frequência relativa.
-

é a frequência absoluta.
-

é o número total de dados.
Por outro lado, para calcular a frequência relativa em percentagem , ou seja, a frequência relativa expressa em percentagem, basta multiplicar a fórmula anterior por 100:
![]()
Exemplos de frequência relativa
Depois de ver a definição de frequência relativa, abaixo estão dois exemplos do mundo real para que você possa ver como esse tipo de frequência é calculado. No primeiro exemplo, é determinada a frequência relativa de uma variável discreta e no segundo exemplo, uma variável contínua.
Exemplo 1: variável discreta
- As notas obtidas na disciplina de estatística numa turma de 30 alunos são as seguintes. Qual é a frequência relativa de cada nota?
![]()
![]()
![]()
A variável neste exercício é discreta porque os dados só podem ser inteiros; portanto, não há necessidade de agrupar os dados em intervalos.
Para encontrar a frequência relativa, devemos primeiro determinar a frequência absoluta. Então construímos uma tabela de frequência e calculamos a frequência absoluta para cada valor diferente:

Agora que calculamos a frequência absoluta, podemos calcular a frequência relativa. Para fazer isso, basta dividir cada frequência absoluta pelo número total de dados (30):
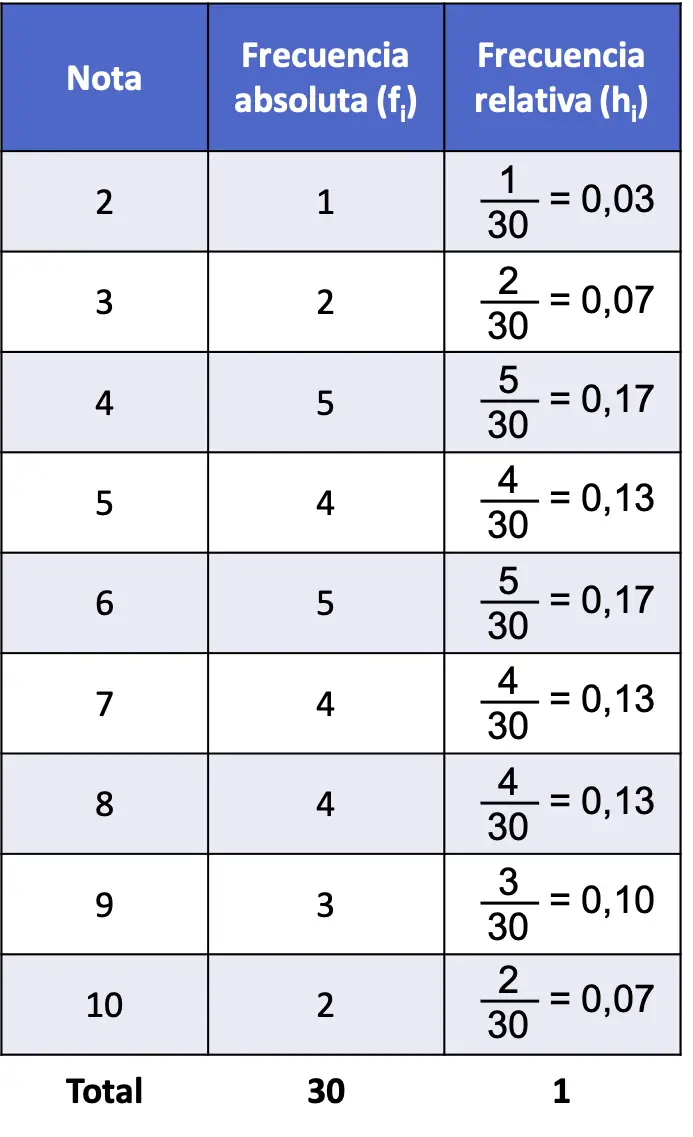
Assim, a tabela de frequência do problema com frequência absoluta e frequência relativa é a seguinte:

Observe que a soma de todas as frequências relativas sempre dá 1, caso contrário isso significa que alguns cálculos estão errados.
Exemplo 2: variável contínua
- A altura de 20 pessoas foi medida e os resultados abaixo foram obtidos. Separe os dados em intervalos e encontre a frequência relativa de cada intervalo.
![]()
![]()
Os dados desta amostra estatística pertencem a uma variável contínua, pois são decimais e portanto a variável pode assumir qualquer valor. Portanto, antes de fazer os cálculos de frequência, primeiro agruparemos os dados em intervalos com amplitude de 10 décimos.
A seguir, fazemos uma tabela de frequência com a frequência absoluta de cada intervalo:

E uma vez encontrada a frequência absoluta, podemos obter a frequência relativa de cada intervalo dividindo sua frequência absoluta pelo número total de dados (20):

Frequência relativa cumulativa
Como o nome sugere, a frequência relativa cumulativa é outro tipo de frequência usada em estatísticas e calculada a partir da frequência relativa.
Mais precisamente, a frequência relativa cumulativa de um valor é igual à soma da frequência relativa do próprio valor mais as frequências relativas de todos os valores menores.
Para que você possa ver como a frequência relativa cumulativa é obtida, a frequência relativa cumulativa do conjunto de dados no primeiro exemplo foi calculada abaixo:
