Como realizar um teste log rank em r

Um teste log-rank é a forma mais comum de comparar curvas de sobrevivência entre dois grupos.

Este teste usa as seguintes suposições :

H ₀ : Não há diferença na sobrevivência entre os dois grupos.

_HA : Há uma diferença na sobrevivência entre os dois grupos.

Se o valor p do teste estiver abaixo de um certo nível de significância (por exemplo, α = 0,05), então podemos rejeitar a hipótese nula e concluir que há evidências suficientes para dizer que há uma diferença na sobrevivência entre os dois grupos.

Para realizar um teste de log-rank em R, podemos usar a função survdiff() do pacote survival , que usa a seguinte sintaxe:

survdiff(Surv(tempo, status) ~ preditores, dados)

Esta função retorna uma estatística de teste qui-quadrado e um valor p correspondente.

O exemplo a seguir mostra como usar esta função para realizar um teste de log-rank em R.

Exemplo: Teste de Log Rank em R

Para este exemplo, usaremos o conjunto de dados ovarianos do pacote de sobrevivência . Este conjunto de dados contém as seguintes informações sobre 26 pacientes:

• Tempo de sobrevivência (em meses) após o diagnóstico de câncer de ovário
• Se o tempo de sobrevivência foi censurado ou não
• Tipo de tratamento recebido (rx = 1 ou rx = 2)

O código a seguir mostra como exibir as primeiras seis linhas deste conjunto de dados:

 library (survival)

#view first six rows of dataset
head(ovarian)

  futime fustat age resid.ds rx ecog.ps
1 59 1 72.3315 2 1 1
2 115 1 74.4932 2 1 1
3 156 1 66.4658 2 1 2
4 421 0 53.3644 2 2 1
5,431 1 50.3397 2 1 1
6 448 0 56.4301 1 1 2

O código a seguir mostra como realizar um teste log-rank para determinar se há diferença na sobrevivência entre pacientes que receberam tratamentos diferentes:

 #perform log rank test
survdiff(Surv(futime, fustat) ~ rx, data=ovarian)

Call:
survdiff(formula = Surv(futime, fustat) ~ rx, data = ovarian)

      N Observed Expected (OE)^2/E (OE)^2/V
rx=1 13 7 5.23 0.596 1.06
rx=2 13 5 6.77 0.461 1.06

 Chisq= 1.1 on 1 degrees of freedom, p= 0.3 

A estatística do teste Qui-quadrado é 1,1 com 1 grau de liberdade e o valor p correspondente é 0,3 . Como esse valor p não é inferior a 0,05, não rejeitamos a hipótese nula.

Por outras palavras, não temos provas suficientes para afirmar que existe uma diferença estatisticamente significativa na sobrevivência entre os dois tratamentos.

Também podemos traçar curvas de sobrevivência para cada grupo usando a seguinte sintaxe:

 #plot survival curves for each treatment group
plot(survfit(Surv(futime, fustat) ~ rx, data = ovarian), 
     xlab = " Time ", 
     ylab = “ Overall survival probability ”)

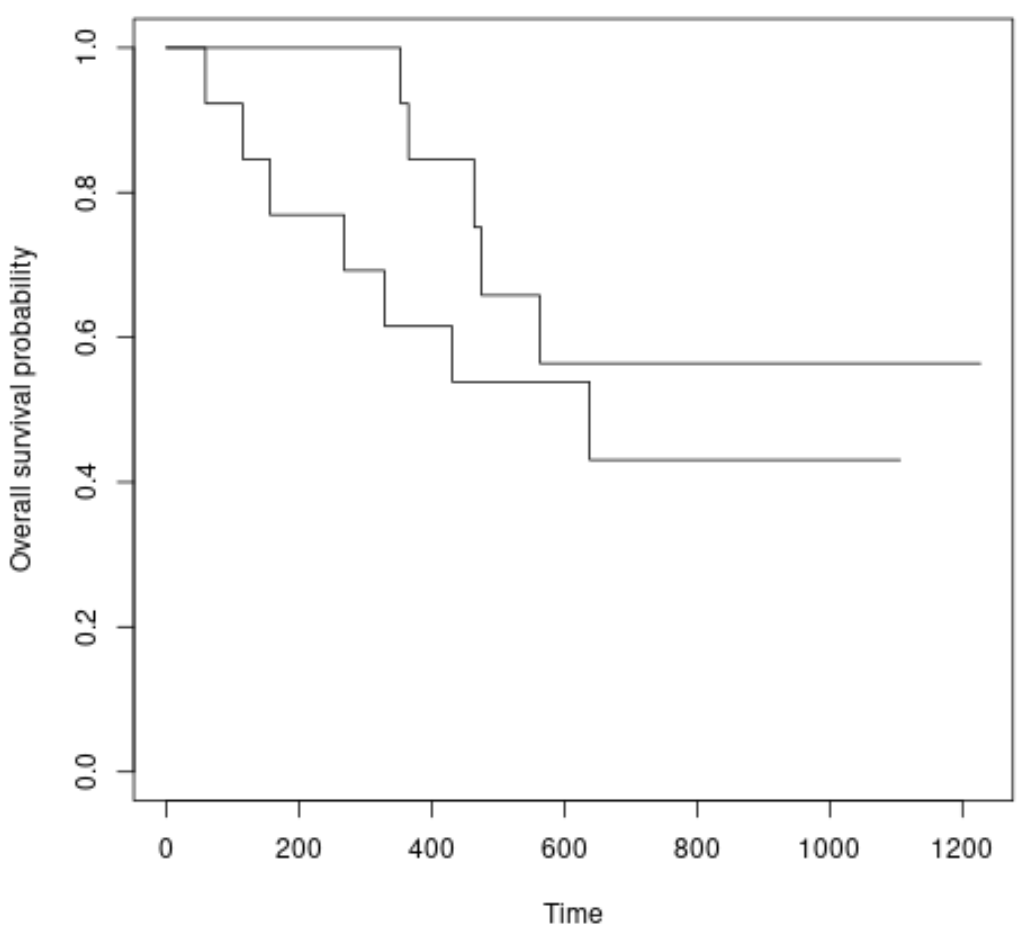
Podemos ver que as curvas de sobrevivência são ligeiramente diferentes, mas o teste log-rank nos disse que a diferença não é estatisticamente significativa.