Como realizar a regressão de potência em r (passo a passo)
A regressão de potência é um tipo de regressão não linear que assume a seguinte forma:
y = axb
Ouro:
- y: a variável de resposta
- x: a variável preditiva
- a, b: os coeficientes de regressão que descrevem a relação entre x e y
Este tipo de regressão é utilizado para modelar situações em que a variável resposta é igual à variável preditora elevada a uma potência.
O exemplo passo a passo a seguir mostra como realizar uma regressão de potência para um determinado conjunto de dados em R.
Etapa 1: crie os dados
Primeiro, vamos criar dados falsos para duas variáveis: x e y.
#create data
x=1:20
y=c(1, 8, 5, 7, 6, 20, 15, 19, 23, 37, 33, 38, 49, 50, 56, 52, 70, 89, 97, 115)
Etapa 2: visualize os dados
A seguir, vamos criar um gráfico de dispersão para visualizar a relação entre x e y:
#create scatterplot
plot(x, y)
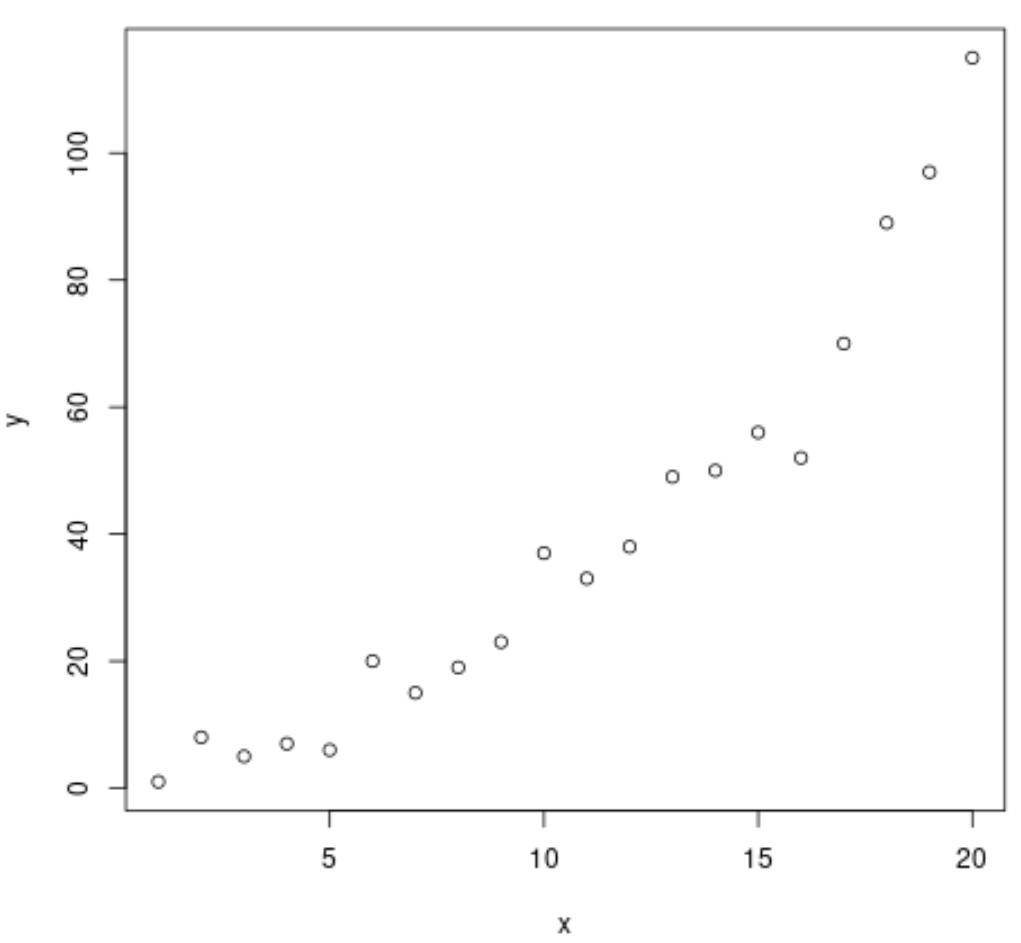
O gráfico mostra que existe uma clara relação de poder entre as duas variáveis. Assim, parece sensato ajustar uma equação de regressão de potência aos dados, em vez de um modelo de regressão linear.
Etapa 3: Ajustar o modelo de regressão de potência
A seguir, usaremos a função lm() para ajustar um modelo de regressão aos dados, especificando que R deve usar a variável de resposta log e a variável preditora log ao ajustar o modelo:
#fit the model model <- lm(log(y)~ log(x)) #view the output of the model summary(model) Call: lm(formula = log(y) ~ log(x)) Residuals: Min 1Q Median 3Q Max -0.67014 -0.17190 -0.05341 0.16343 0.93186 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.15333 0.20332 0.754 0.461 log(x) 1.43439 0.08996 15.945 4.62e-12 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.3187 on 18 degrees of freedom Multiple R-squared: 0.9339, Adjusted R-squared: 0.9302 F-statistic: 254.2 on 1 and 18 DF, p-value: 4.619e-12
O valor F geral do modelo é 252,1 e o valor p correspondente é extremamente baixo (4,619e-12), indicando que o modelo como um todo é útil.
Usando os coeficientes da tabela de saída, podemos ver que a equação de regressão de potência ajustada é:
ln(y) = 0,15333 + 1,43439ln(x)
Aplicando e a ambos os lados, podemos reescrever a equação da seguinte forma:
- y = e 0,15333 + 1,43439ln(x)
- y = 1,1657x 1,43439
Podemos usar esta equação para prever a variável de resposta, y , com base no valor da variável preditora, x .
Por exemplo, se x = 12, então preveríamos que y seria 41,167 :
y = 1,1657(12) 1,43439 = 41,167
Bônus: sinta-se à vontade para usar esta calculadora de regressão de potência online para calcular automaticamente a equação de regressão de potência para um determinado preditor e variável de resposta.
Recursos adicionais
Como realizar regressão linear múltipla em R
Como realizar regressão exponencial em R
Como realizar regressão logarítmica em R