Como realizar anova aninhada em r (passo a passo)

Uma ANOVA aninhada é um tipo de ANOVA (“análise de variância”) em que pelo menos um fator está aninhado dentro de outro fator.

Por exemplo, suponha que um pesquisador queira saber se três fertilizantes diferentes produzem níveis diferentes de crescimento das plantas.

Para testar isso, três técnicos diferentes borrifam fertilizante A em quatro plantas, três outros técnicos borrifam fertilizante B em quatro plantas e três outros técnicos borrifam fertilizante C em quatro plantas.

Neste cenário, a variável resposta é o crescimento da planta e os dois fatores são técnico e fertilizante. Acontece que o técnico está aninhado no fertilizante:

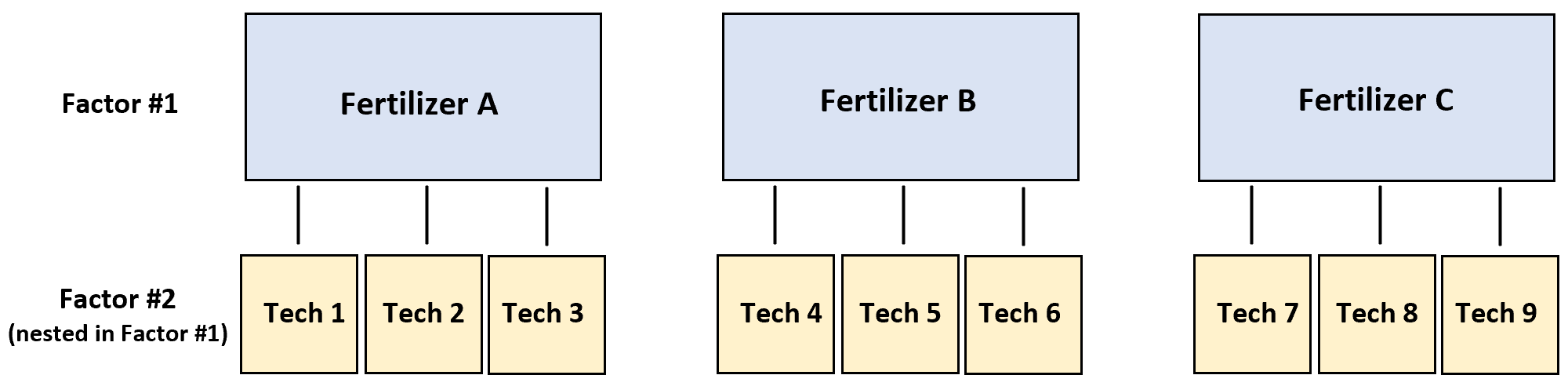
O exemplo passo a passo a seguir mostra como realizar esta ANOVA aninhada em R.

Etapa 1: crie os dados

Primeiro, vamos criar um data frame para armazenar nossos dados em R:

 #create data
df <- data. frame (growth=c(13, 16, 16, 12, 15, 16, 19, 16, 15, 15, 12, 15,
                          19, 19, 20, 22, 23, 18, 16, 18, 19, 20, 21, 21,
                          21, 23, 24, 22, 25, 20, 20, 22, 24, 22, 25, 26),
                 fertilizer=c(rep(c(' A ', ' B ', ' C '), each= 12 )),
                 tech=c(rep(1:9, each= 4 )))

#view first six rows of data
head(df)

  growth fertilizer tech
1 13 A 1
2 16 A 1
3 16 A 1
4 12 A 1
5 15 A 2
6 16 A 2

Etapa 2: ajustar ANOVA aninhada

Podemos usar a seguinte sintaxe para ajustar uma ANOVA aninhada em R:

aov(resposta ~ fator A / fator B)

Ouro:

• resposta: a variável de resposta
• fator A: o primeiro fator
• fator B: o segundo fator aninhado no primeiro fator

O código a seguir mostra como ajustar a ANOVA aninhada para nosso conjunto de dados:

 #fit nested ANOVA
nest <- aov(df$growth ~ df$fertilizer / factor(df$tech))

#view summary of nested ANOVA
summary(nest)

                              Df Sum Sq Mean Sq F value Pr(>F)    
df$fertilizer 2 372.7 186.33 53.238 4.27e-10 ***
df$fertilizer:factor(df$tech) 6 31.8 5.31 1.516 0.211    
Residuals 27 94.5 3.50                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Etapa 3: interprete o resultado

Podemos observar a coluna do valor p para determinar se cada fator tem ou não um efeito estatisticamente significativo no crescimento das plantas.

Na tabela acima, podemos ver que o fertilizante tem um efeito estatisticamente significativo no crescimento das plantas (valor p < 0,05), mas o técnico não (valor p = 0,211).

Isto diz-nos que se quisermos aumentar o crescimento das plantas, precisamos de nos concentrar no fertilizante utilizado e não no técnico individual que aplica o fertilizante.

Etapa 4: visualize os resultados

Finalmente, podemos usar boxplots para visualizar a distribuição do crescimento das plantas por fertilizante e por técnico:

 #load ggplot2 data visualization package
library (ggplot2)

#create boxplots to visualize plant growth
ggplot(df, aes (x=factor(tech), y=growth, fill=fertilizer)) +
  geom_boxplot()

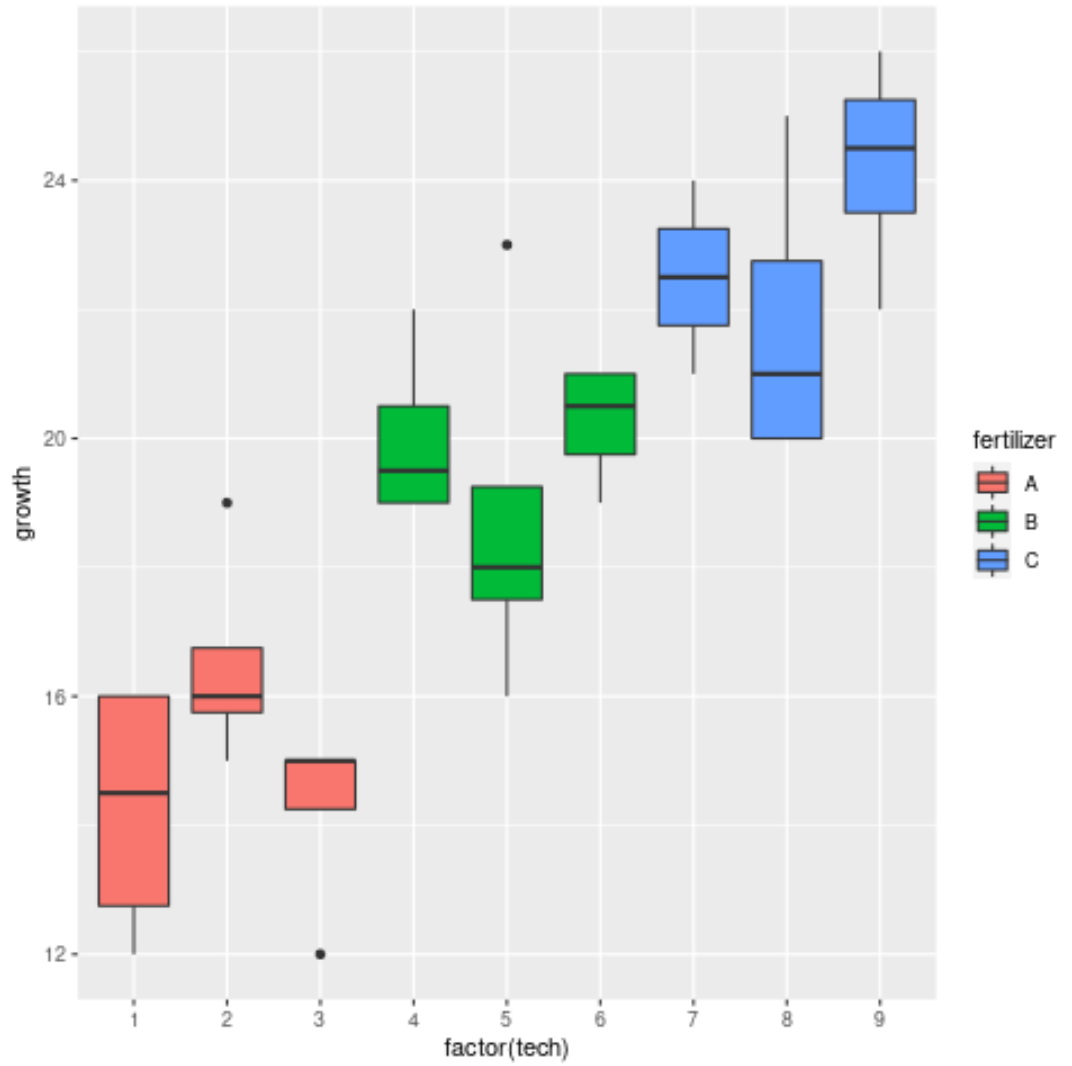
O gráfico mostra que há uma variação significativa no crescimento entre os três fertilizantes diferentes, mas não tanta variação entre os técnicos dentro de cada grupo de fertilizantes.

Isto parece corresponder aos resultados da ANOVA aninhada e confirma que os fertilizantes têm um efeito significativo no crescimento das plantas, mas os técnicos individuais não.

Recursos adicionais

Como realizar ANOVA unidirecional em R
Como realizar ANOVA bidirecional em R
Como realizar ANOVA de medidas repetidas em R