O que é regressão curvilínea? (definição e exemplos)

Regressão curvilínea é o nome dado a qualquer modelo de regressão que tenta ajustar uma curva em vez de uma linha reta.

Exemplos comuns de modelos de regressão curvilínea incluem:

Regressão quadrática: usada quando existe uma relação quadrática entre uma variável preditora e uma variável resposta . Quando representado graficamente, esse tipo de relacionamento se parece com um “U” ou um “U” invertido em um gráfico de dispersão:

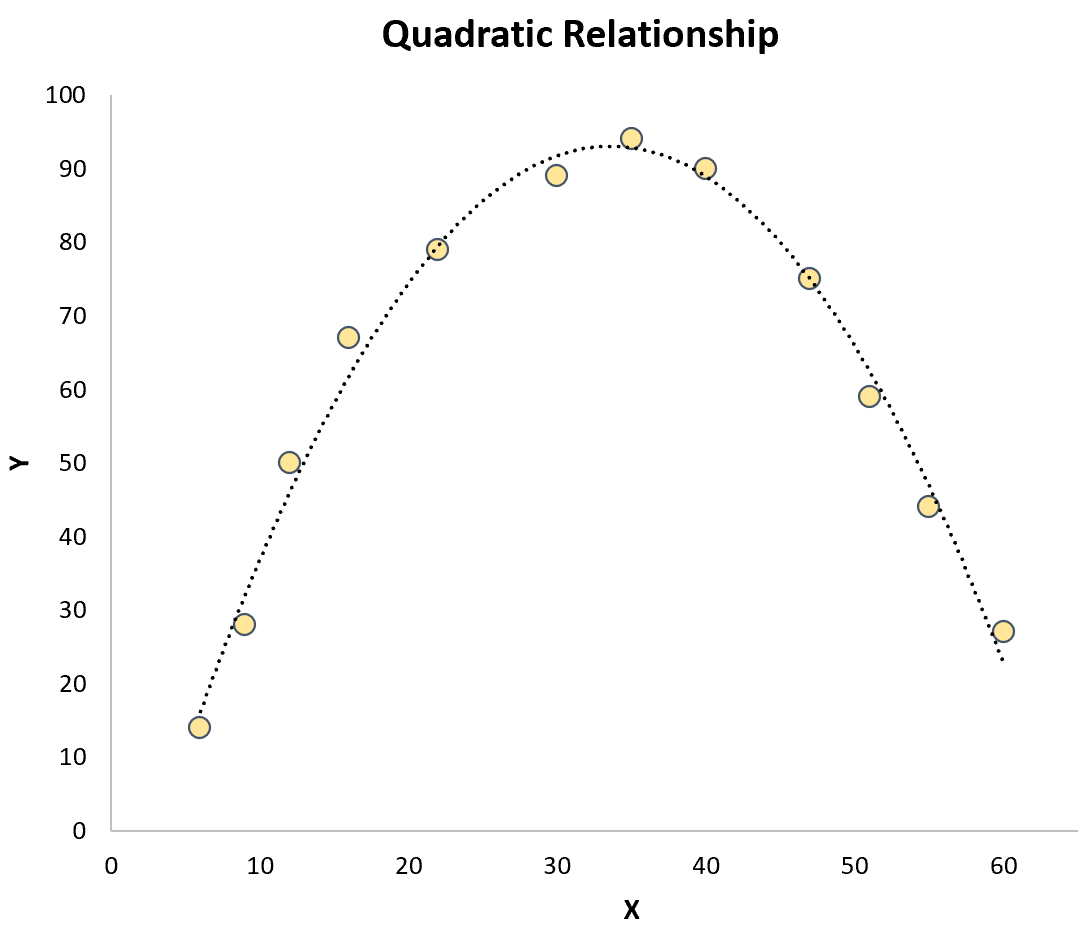
Regressão Cúbica: Usada quando existe um relacionamento cúbico entre uma variável preditora e uma variável de resposta. Quando representado graficamente, esse tipo de relacionamento mostra duas curvas distintas em um gráfico de dispersão:

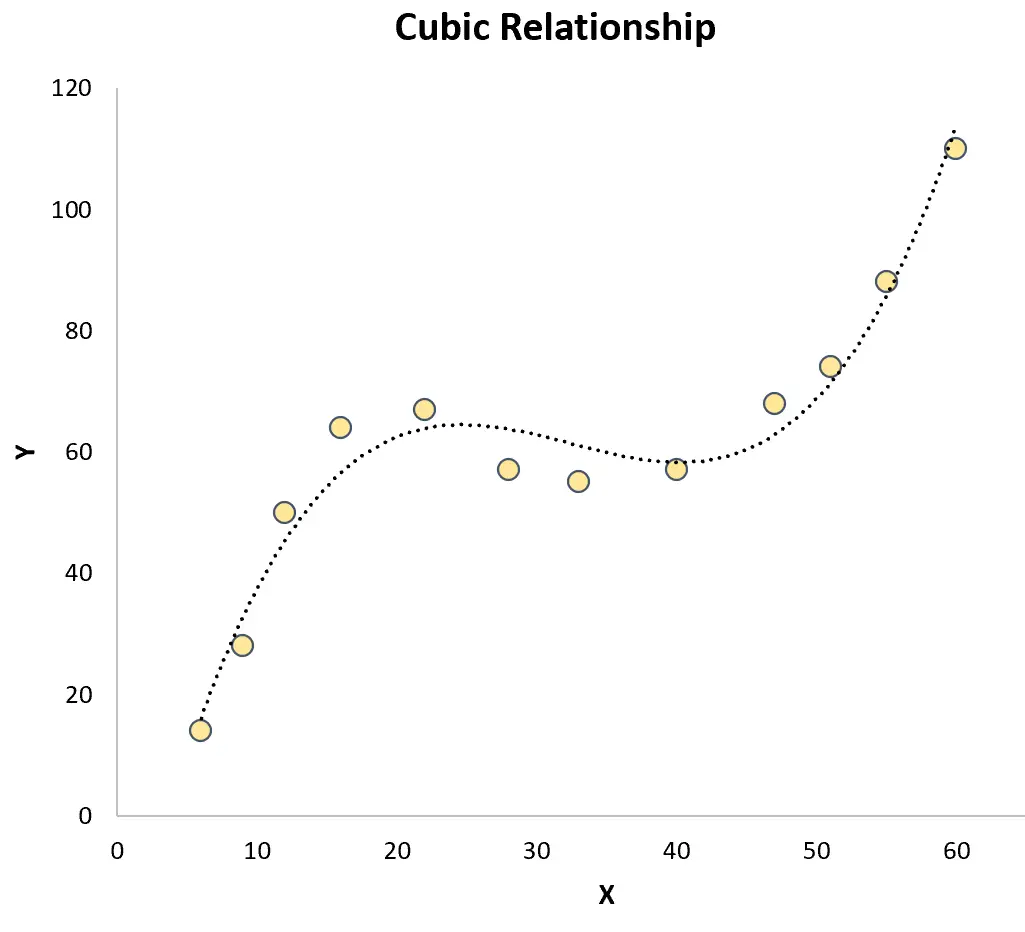
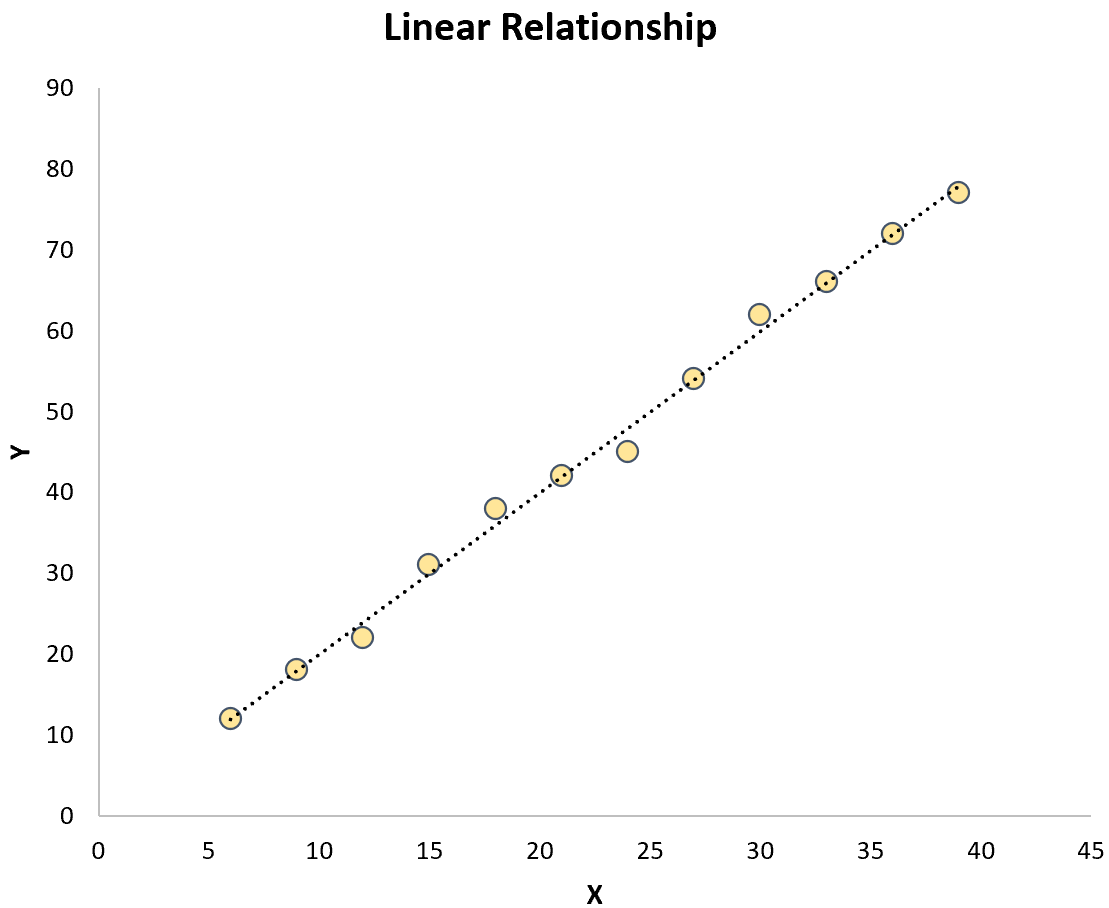
Ambos contrastam com a regressão linear simples em que a relação entre a variável preditora e a variável resposta é linear:

A fórmula para modelos de regressão curvilínea

Um modelo de regressão linear simples tenta ajustar um conjunto de dados usando a seguinte fórmula:

ŷ = β ₀ + β ₁ x

Ouro:

• ŷ: A variável de resposta
• β ₀ , β ₁ : Os coeficientes de regressão
• x: a variável preditiva

Em contraste, um modelo de regressão quadrática utiliza a seguinte fórmula:

ŷ = β ₀ + β ₁ x + β ₂ x ²

E um modelo de regressão cúbica usa a seguinte fórmula:

ŷ = β ₀ + β ₁ x + β ₂ x ² + β ₃ x ³

Um nome mais geral dado aos modelos de regressão que incluem expoentes é regressão polinomial , que leva a seguinte fórmula:

ŷ = β ₀ + β ₁ x + β ₂ x ² + … + β _k x ^k

O valor de k indica o grau do polinômio. Embora o grau possa ser qualquer número positivo, na prática raramente ajustamos modelos de regressão polinomial com grau superior a 3 ou 4.

Ao usar expoentes na fórmula do modelo de regressão, os modelos de regressão polinomial são capazes de ajustar curvas aos conjuntos de dados em vez de linhas retas.

Quando usar regressão curvilínea

A maneira mais fácil de saber se você deve ou não usar a regressão curvilínea é criar um gráfico de dispersão da variável preditora e da variável resposta.

Se o gráfico de dispersão mostrar uma relação linear entre as duas variáveis, uma regressão linear simples será provavelmente apropriada.

No entanto, se o gráfico de dispersão mostrar um padrão quadrático, cúbico ou outro padrão curvilíneo entre o preditor e a variável de resposta, então a regressão curvilínea é provavelmente mais apropriada para uso.

Você também pode ajustar um modelo de regressão linear simples e um modelo de regressão curvilínea e comparar os valores de R ao quadrado ajustados de cada modelo para determinar qual modelo fornece o melhor ajuste aos dados.

O R-quadrado ajustado é útil porque informa quanto da variância na variável de resposta pode ser explicada pela(s) variável(ões) preditora(s), ajustada(s) para o número de variáveis preditoras no modelo.

Em geral, o modelo com o maior valor de R-quadrado ajustado proporciona um melhor ajuste ao conjunto de dados.

Recursos adicionais

Os tutoriais a seguir explicam como realizar regressão polinomial em diferentes softwares estatísticos:

Uma introdução à regressão polinomial
Como realizar regressão polinomial no Excel
Como realizar regressão polinomial em Python
Como realizar regressão polinomial em R