Como realizar uma regressão robusta em r (passo a passo)

A regressão robusta é um método que podemos usar como alternativa à regressão de mínimos quadrados comum quando há valores discrepantes ou observações influentes no conjunto de dados com o qual estamos trabalhando.

Para realizar regressão robusta em R, podemos usar a função rlm() do pacote MASS , que usa a seguinte sintaxe:

O exemplo passo a passo a seguir mostra como realizar uma regressão robusta em R para um determinado conjunto de dados.

Etapa 1: crie os dados

Primeiro, vamos criar um conjunto de dados falso para trabalhar:

 #create data
df <- data. frame (x1=c(1, 3, 3, 4, 4, 6, 6, 8, 9, 3,
                      11, 16, 16, 18, 19, 20, 23, 23, 24, 25),
                 x2=c(7, 7, 4, 29, 13, 34, 17, 19, 20, 12,
                      25, 26, 26, 26, 27, 29, 30, 31, 31, 32),
                  y=c(17, 170, 19, 194, 24, 2, 25, 29, 30, 32,
                      44, 60, 61, 63, 63, 64, 61, 67, 59, 70))

#view first six rows of data
head(df)

  x1 x2 y
1 1 7 17
2 3 7 170
3 3 4 19
4 4 29 194
5 4 13 24
6 6 34 2

Etapa 2: realizar a regressão de mínimos quadrados comuns

A seguir, vamos ajustar um modelo de regressão de mínimos quadrados ordinário e criar um gráfico dos resíduos padronizados .

Na prática, muitas vezes consideramos qualquer resíduo padronizado cujo valor absoluto seja superior a 3 como um valor atípico.

 #fit ordinary least squares regression model
ols <- lm(y~x1+x2, data=df)

#create plot of y-values vs. standardized residuals
plot(df$y, rstandard(ols), ylab=' Standardized Residuals ', xlab=' y ') 
abline(h= 0 ) 

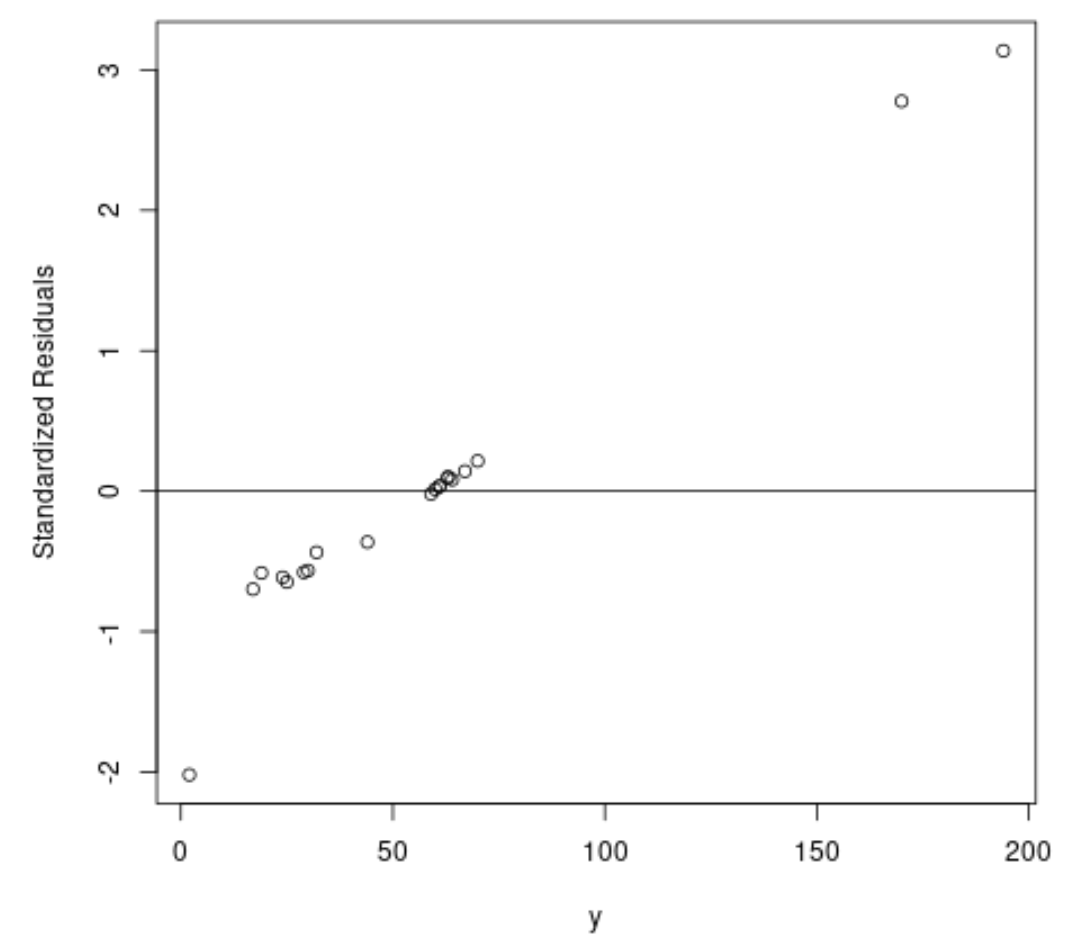
No gráfico podemos ver que existem duas observações com resíduos padronizados em torno de 3.

Isto indica que existem dois valores discrepantes potenciais no conjunto de dados e, portanto, podemos nos beneficiar de uma regressão robusta.

Etapa 3: realizar regressão robusta

A seguir, vamos usar a função rlm() para ajustar um modelo de regressão robusto:

 library (MASS)

#fit robust regression model
robust <- rlm(y~x1+x2, data=df)

Para determinar se este modelo de regressão robusto proporciona um melhor ajuste aos dados em comparação com o modelo OLS, podemos calcular o erro padrão residual de cada modelo.

O erro padrão residual (RSE) é uma forma de medir o desvio padrão dos resíduos em um modelo de regressão. Quanto menor o valor de CSR, melhor o modelo será capaz de ajustar os dados.

O código a seguir mostra como calcular o RSE para cada modelo:

 #find residual standard error of ols model
summary(ols)$sigma

[1] 49.41848

#find residual standard error of ols model
summary(robust)$sigma

[1] 9.369349

Podemos ver que o RSE do modelo de regressão robusto é muito inferior ao do modelo de regressão de mínimos quadrados ordinário, o que nos diz que o modelo de regressão robusto fornece um melhor ajuste aos dados.

Recursos adicionais

Como realizar regressão linear simples em R
Como realizar regressão linear múltipla em R
Como realizar regressão polinomial em R