O que é considerado “fraco”; correlação?
Nas estatísticas, muitas vezes procuramos compreender como duas variáveis se relacionam entre si. Por exemplo, podemos querer saber:
- Qual é a relação entre o número de horas que um aluno estuda e a nota que recebe no exame?
- Qual é a relação entre a temperatura externa e a quantidade de barras de sorvete vendidas por um food truck?
- Qual é a relação entre o dinheiro gasto em publicidade e a receita total obtida por um determinado negócio?
Em cada cenário, queremos entender a relação entre duas variáveis.
Uma das formas mais comuns de quantificar uma relação entre duas variáveis é usar o coeficiente de correlação de Pearson , que é uma medida da associação linear entre duas variáveis.
Sempre assume um valor entre -1 e 1 onde:
- -1 indica uma correlação linear perfeitamente negativa entre duas variáveis
- 0 indica nenhuma correlação linear entre duas variáveis
- 1 indica uma correlação linear perfeitamente positiva entre duas variáveis
Freqüentemente denotado por r , esse número nos ajuda a compreender a força da relação entre duas variáveis. Quanto mais próximo r estiver de zero, mais fraca será a relação entre as duas variáveis .
É importante notar que duas variáveis podem ter uma correlação positiva fraca ou uma correlação negativa fraca.
Correlação positiva fraca: quando uma variável aumenta, a outra variável tende a aumentar também, mas apenas de forma fraca ou pouco confiável.
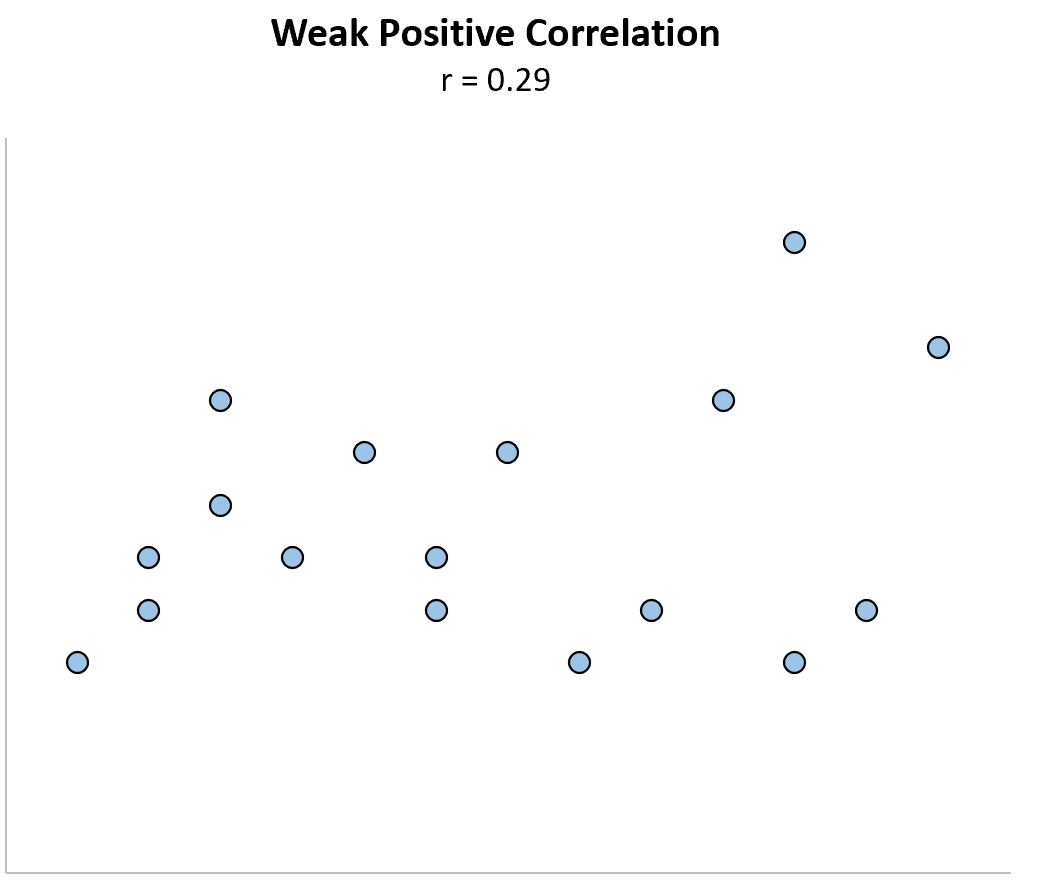
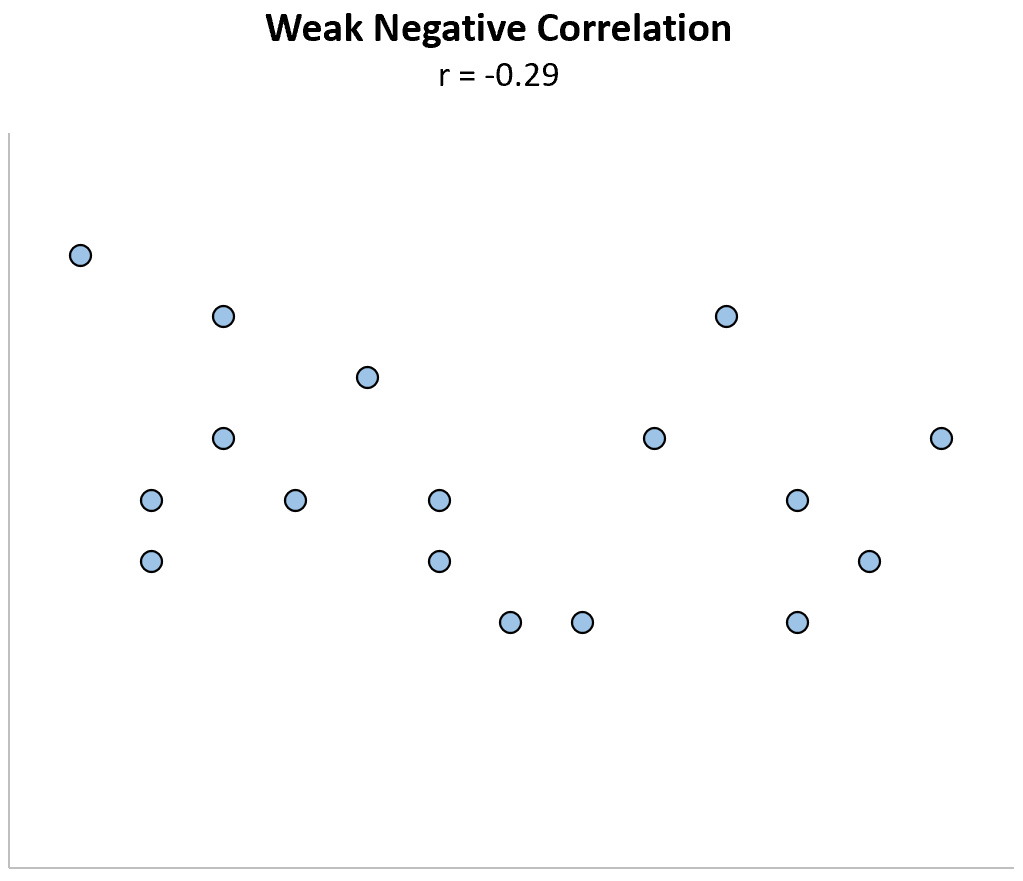
Correlação negativa baixa: quando uma variável aumenta, a outra variável tende a diminuir, mas apenas de forma fraca ou pouco confiável.
A tabela a seguir mostra a regra prática para interpretar a força do relacionamento entre duas variáveis com base no valor de r :
| Valor absoluto de r | Força do relacionamento |
|---|---|
| r < 0,25 | Sem relacionamento |
| 0,25 < r < 0,5 | Relacionamento fraco |
| 0,5 < r < 0,75 | Relacionamentos moderados |
| r > 0,75 | Relacionamentos fortes |
A correlação entre duas variáveis é considerada baixa se o valor absoluto de r estiver entre 0,25 e 0,5.
No entanto, a definição de correlação “fraca” pode variar de campo para campo.
Médico
Nas áreas médicas, a definição de relacionamento “fraco” costuma ser muito mais baixa. Se a relação entre tomar um determinado medicamento e a redução de ataques cardíacos for r = 0,2, isso pode ser considerado “nenhuma relação” em outras áreas, mas na medicina é suficientemente significativo para que valha a pena tomar o medicamento para reduzir o risco de ataques cardíacos. . sofrer um ataque cardíaco.
Recursos Humanos
Em uma área como a de recursos humanos, correlações mais baixas também são usadas com mais frequência. Por exemplo, a correlação entre o GPA da faculdade e o desempenho no trabalho demonstrou ser de aproximadamente r = 0,16 . Isso é muito baixo, mas é importante o suficiente para que uma empresa pelo menos considere isso durante um processo de entrevista.
Tecnologia
Nas áreas de tecnologia, a correlação entre as variáveis pode precisar ser muito maior para ser considerada “baixa”. Por exemplo, se uma empresa cria um carro autônomo e a correlação entre as decisões de direção do carro e a probabilidade de evitar um acidente é r = 0,95 , esta pode ser considerada uma correlação “fraca” e provavelmente é fraca demais para o carro ser considerado seguro, pois uma decisão errada pode ser fatal.
Use gráficos de dispersão para visualizar correlações
Ao calcular o coeficiente de correlação entre duas variáveis, é útil criar um gráfico de dispersão para visualizar também a correlação.
Em particular, as nuvens de pontos oferecem duas vantagens:
1. Os gráficos de dispersão podem ajudá-lo a identificar valores discrepantes que afetam o coeficiente de correlação.
Um valor discrepante extremo pode ter um grande impacto no coeficiente de correlação. Considere o exemplo abaixo, em que as variáveis X e Y possuem um coeficiente de correlação de Pearson de r = 0,91 .
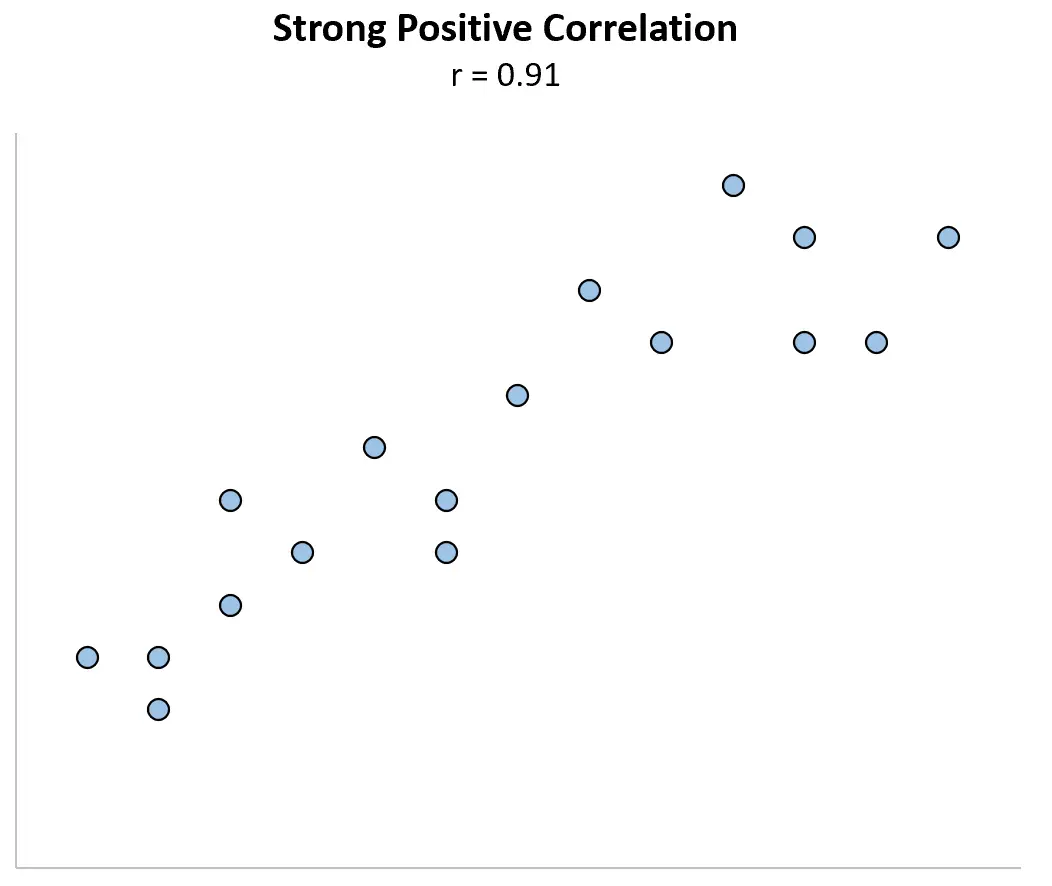
Agora imagine que alteramos o primeiro ponto de dados para ser muito maior. O coeficiente de correlação torna-se repentinamente r = 0,29 .
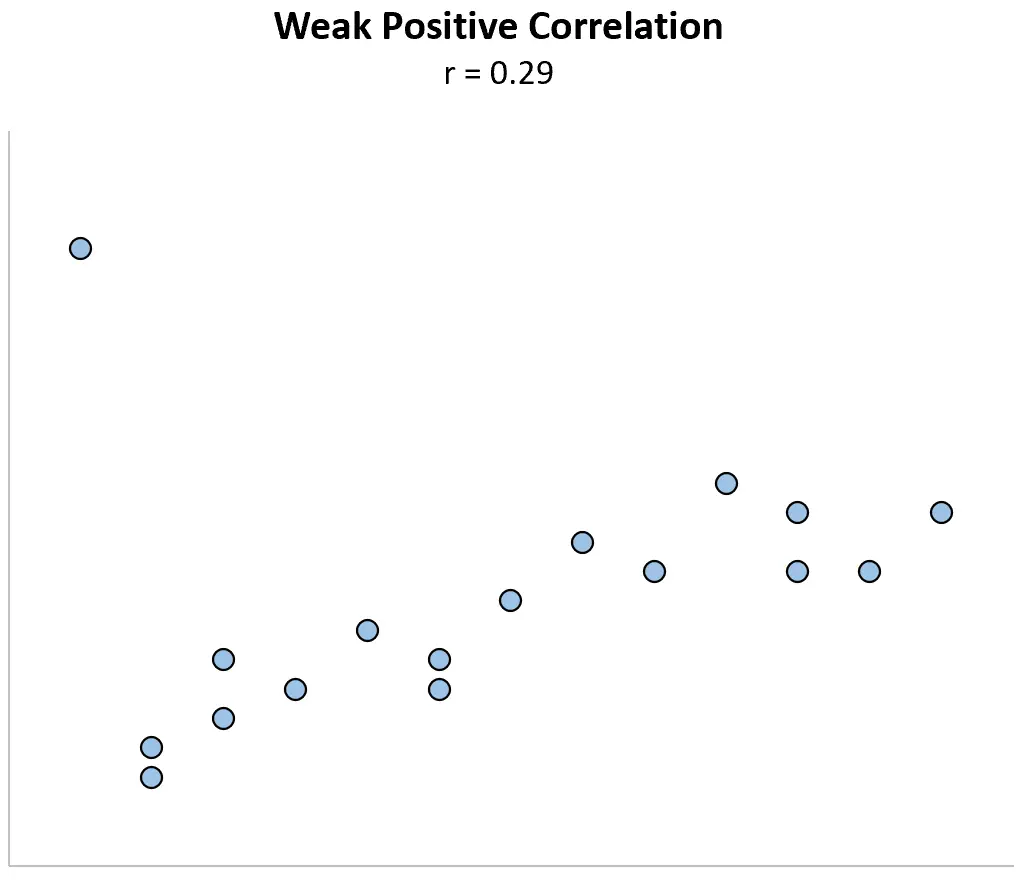
Este único ponto de dados altera o coeficiente de correlação de uma relação fortemente positiva para uma relação fracamente positiva.
(2) Os gráficos de dispersão podem ajudá-lo a identificar relações não lineares entre variáveis.
Um coeficiente de correlação de Pearson simplesmente nos diz se duas variáveis estão linearmente relacionadas. Mas mesmo que um coeficiente de correlação de Pearson nos diga que duas variáveis não estão correlacionadas, ainda poderão ter algum tipo de relação não linear.
Por exemplo, considere o gráfico de dispersão abaixo entre as variáveis X e Y , em que sua correlação é r = 0,00 .
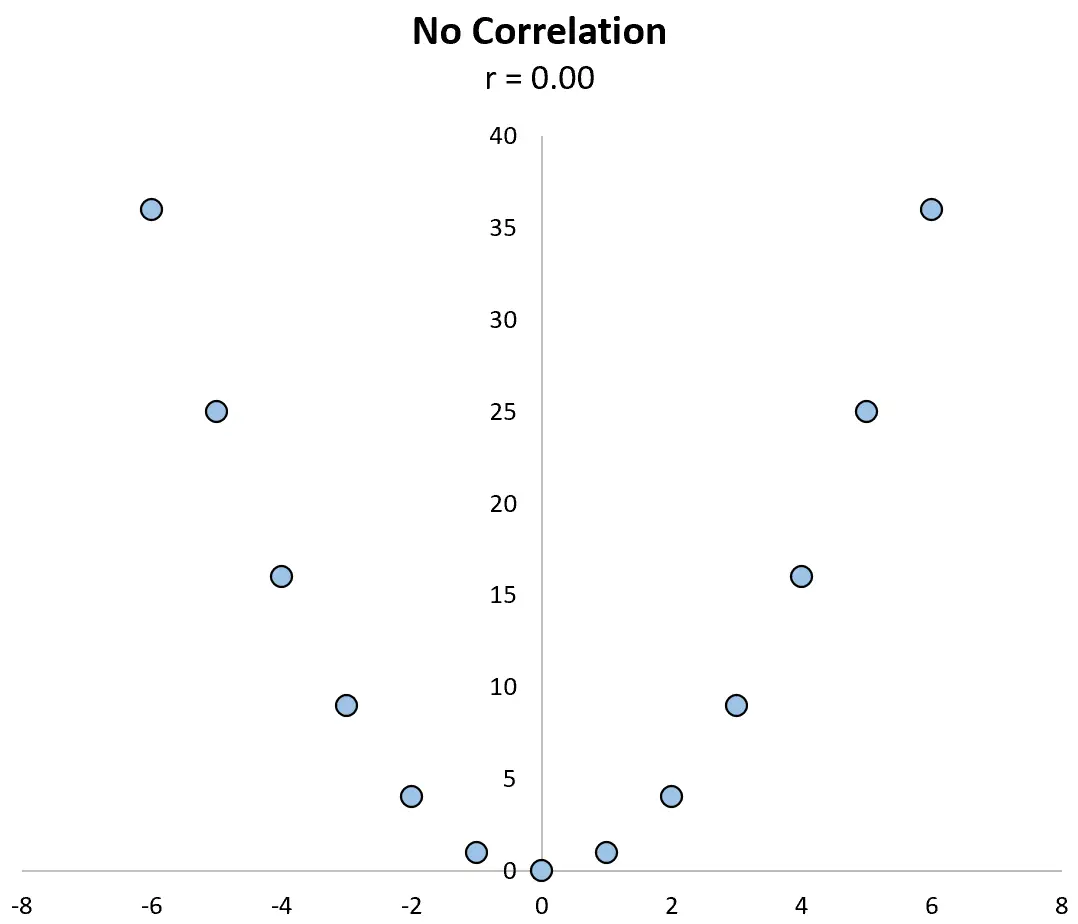
As variáveis claramente não têm uma relação linear, mas têm uma relação não linear: os valores de y são simplesmente os valores de x ao quadrado.
Um coeficiente de correlação por si só não poderia detectar esta relação, mas um gráfico de dispersão poderia.
Conclusão
Resumindo:
1. Geralmente, um coeficiente de correlação entre 0,25 e 0,5 é considerado uma correlação “fraca” entre duas variáveis.
2. Esta regra prática pode variar de área para área. Por exemplo, uma correlação muito mais baixa pode ser considerada fraca numa área médica em comparação com uma área tecnológica. Certifique-se de usar seu conhecimento no assunto para decidir o que é considerado baixa correlação.
3. Ao usar um coeficiente de correlação para descrever o relacionamento entre duas variáveis, também é útil criar um gráfico de dispersão para que você possa identificar valores discrepantes no conjunto de dados, bem como um possível relacionamento não linear.
Recursos adicionais
O que é considerado uma correlação “forte”?
Calculadora de Matriz de Correlação
Correlação vs. associação: qual é a diferença?