Como interpretar a raiz do erro quadrático médio (rmse)
A análise de regressão é uma técnica que podemos usar para compreender a relação entre uma ou mais variáveis preditoras e uma variável de resposta .
Uma maneira de avaliar quão bem um modelo de regressão se ajusta a um conjunto de dados é calcular o erro quadrático médio , que é uma métrica que nos informa a distância média entre os valores previstos do modelo e os valores reais do conjunto de dados.
Quanto menor o RMSE, melhor um determinado modelo é capaz de “ajustar” um conjunto de dados.
A fórmula para encontrar o erro quadrático médio, frequentemente abreviado como RMSE , é:
RMSE = √ Σ(P i – O i ) 2 / n
Ouro:
- Σ é um símbolo sofisticado que significa “soma”
- Pi é o valor previsto para a i-ésima observação no conjunto de dados
- O i é o valor observado para a i-ésima observação no conjunto de dados
- n é o tamanho da amostra
O exemplo a seguir mostra como interpretar o RMSE para um determinado modelo de regressão.
Exemplo: como interpretar o RMSE para um modelo de regressão
Suponha que queiramos construir um modelo de regressão que utilize “horas estudadas” para prever a “nota do exame” dos alunos em um determinado vestibular.
Coletamos os seguintes dados de 15 alunos:
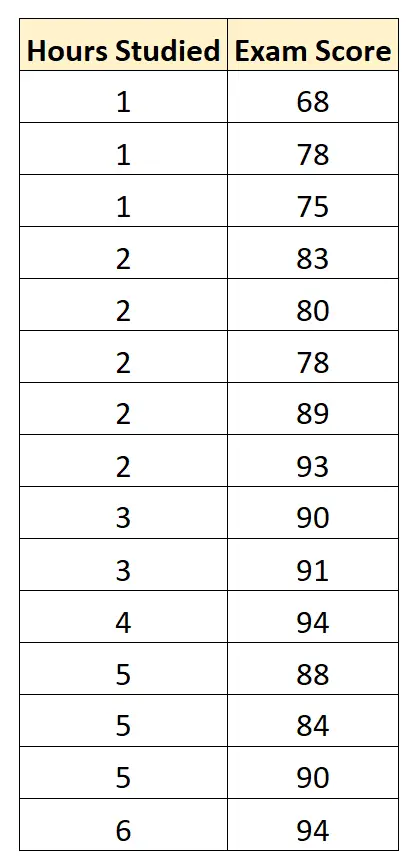
Em seguida, usamos software estatístico (como Excel, SPSS, R, Python), etc. para encontrar o seguinte modelo de regressão ajustado:
Nota do exame = 75,95 + 3,08* (horas estudadas)
Podemos então usar esta equação para prever a nota de cada aluno no exame, com base no número de horas que estudaram:
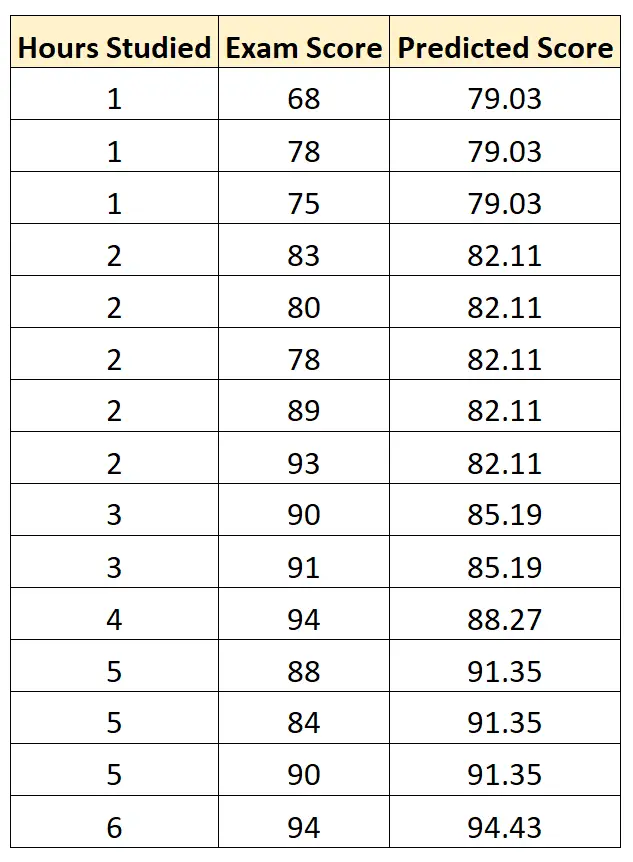
Podemos então calcular a diferença quadrática entre cada pontuação prevista no exame e a pontuação real do exame. Podemos então tirar a raiz quadrada da média dessas diferenças:
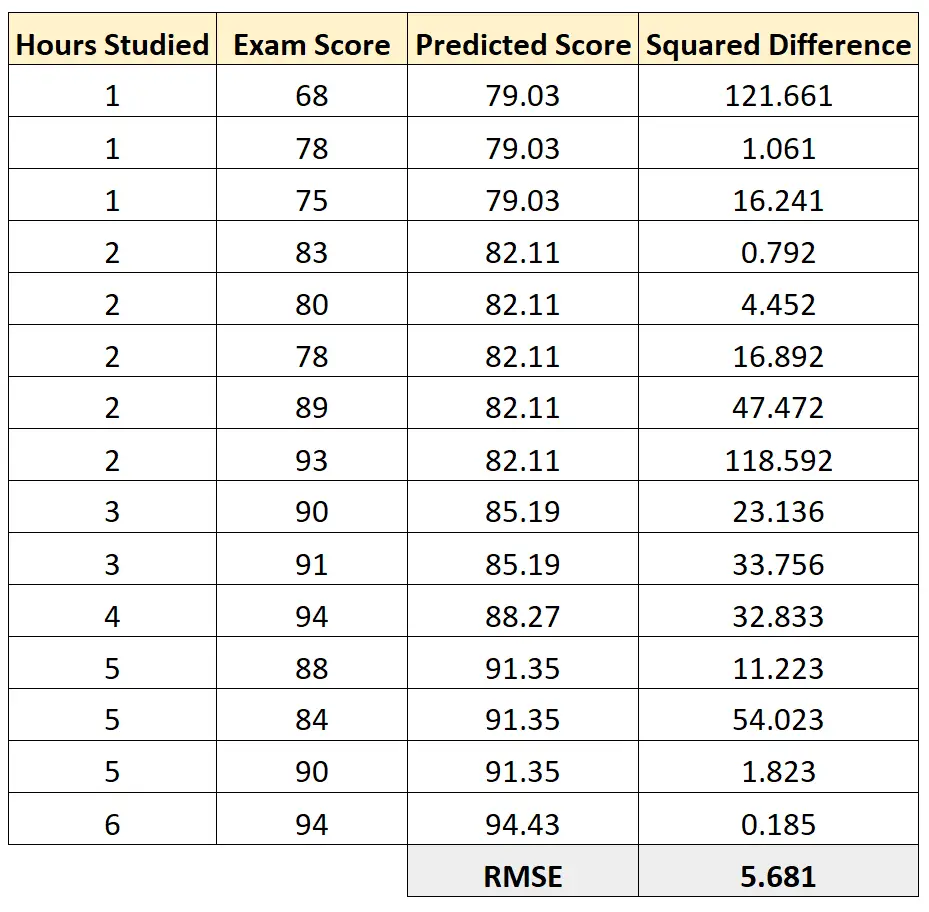
O RMSE deste modelo de regressão é 5,681 .
Lembre-se de que os resíduos de um modelo de regressão são as diferenças entre os valores dos dados observados e os valores previstos do modelo.
Residual = (P i – O i )
Ouro
- Pi é o valor previsto para a i-ésima observação no conjunto de dados
- O i é o valor observado para a i-ésima observação no conjunto de dados
E lembre-se que o RMSE de um modelo de regressão é calculado da seguinte forma:
RMSE = √ Σ(P i – O i ) 2 / n
Isto significa que o RMSE representa a raiz quadrada da variância dos resíduos.
Este é um valor útil de saber porque nos dá uma ideia da distância média entre os valores dos dados observados e os valores dos dados previstos.
Isso contrasta com o R-quadrado do modelo, que nos diz quanto da variância na variável de resposta pode ser explicada pela(s) variável(ões) preditora(s) do modelo.
Comparação de valores RMSE de diferentes modelos
O RMSE é particularmente útil para comparar o ajuste de diferentes modelos de regressão.
Por exemplo, suponha que queremos construir um modelo de regressão para prever as notas dos alunos nos exames e queremos encontrar o melhor modelo possível entre vários modelos potenciais.
Suponha que ajustemos três modelos de regressão diferentes e encontremos seus valores RMSE correspondentes:
- RMSE do modelo 1: 14,5
- RMSE do modelo 2: 16,7
- RMSE do modelo 3: 9,8
O modelo 3 tem o RMSE mais baixo, o que nos diz que é capaz de ajustar melhor o conjunto de dados entre os três modelos potenciais.
Recursos adicionais
Calculadora RMSE
Como calcular RMSE no Excel
Como calcular RMSE em R
Como calcular RMSE em Python