Frequência (estatística)

Este artigo explica o que é a noção de frequência nas estatísticas. Assim, você encontrará a definição de frequência nas estatísticas, os diferentes tipos de frequências que existem e, por fim, como criar uma tabela de frequências.

O que é frequência nas estatísticas?

Nas estatísticas, frequência é o número de vezes que um valor aparece em um conjunto de dados. Simplificando, frequência é o número de vezes que um valor é repetido em uma amostra estatística.

Por exemplo, se numa pesquisa cinco pessoas responderam que a sua cor favorita é o azul, então a frequência da cor azul é igual a 5.

Geralmente, nas estatísticas, a letra f com índice i é usada para representar a frequência do valor i , portanto o símbolo da frequência é _fi .

A soma de todas as frequências fornece o número total de dados na amostra. Portanto, a seguinte fórmula é sempre válida para qualquer estudo estatístico:

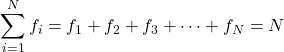
Ouro

é a frequência do valor

E

é o número total de observações.

Tipos de frequências nas estatísticas

Nas estatísticas, os diferentes tipos de frequências são os seguintes:

• Frequência absoluta : corresponde ao número de vezes que um valor aparece em uma amostra estatística.
• Frequência Absoluta Cumulativa : Calculada somando a frequência absoluta do valor mais as frequências absolutas de todos os valores menores.
• Frequência relativa : esta é a frequência absoluta dividida pelo número total de dados.
• Frequência relativa cumulativa : é igual à soma da frequência relativa do valor mais as frequências relativas de todos os valores inferiores.

Na seção abaixo você pode ver como cada tipo de frequência é calculado.

Tabela de frequência

Normalmente, nas estatísticas, os cálculos das frequências de uma amostra de dados são resumidos em uma tabela de frequências. Abaixo está um exemplo passo a passo para que você possa ver como fazer.

• As notas obtidas na disciplina de estatística numa turma de 30 alunos são as seguintes. Construa uma tabela de frequência do conjunto de dados.

Como todos os números só podem ser inteiros, é uma variável discreta. Portanto, não é necessário agrupar os dados em intervalos.

Portanto, precisamos construir uma tabela na qual cada valor diferente será uma linha. Além disso, precisamos encontrar a frequência absoluta de cada valor, para isso basta contar o número de vezes que o valor aparece na amostra de dados.

Observe que a soma de todas as frequências absolutas é igual ao número total de dados. Se esta regra não for respeitada, significa que você se esqueceu de fornecer algumas informações.

Agora que sabemos a frequência absoluta, precisamos de determinar a frequência absoluta cumulativa. Para este cálculo temos duas opções: ou somamos a frequência absoluta do valor mais todas as frequências absolutas dos menores valores, ou pelo contrário, somamos a frequência absoluta do valor mais a frequência absoluta acumulada do valor anterior.

A frequência absoluta acumulada do último valor sempre corresponde ao número total de dados, você pode usar este truque para verificar se os cálculos estão corretos.

A seguir, precisamos determinar a frequência relativa, que é calculada dividindo a frequência absoluta pelo número total de pontos de dados (30):

Tenha em mente que a soma de todas as frequências relativas é sempre igual a 1, caso contrário significa que alguns cálculos da tabela de frequências estão errados.

Por fim, basta extrair a frequência relativa acumulada. Para isso, deve-se somar a frequência relativa do valor em questão mais todas as frequências relativas anteriores ou, o que dá no mesmo, a frequência relativa acumulada anterior:

Resumindo, a tabela de frequências com todas as frequências dos dados problemáticos é a seguinte: