Distribuição de frequência

Este artigo explica o que são distribuições de frequência e como elas são alcançadas. Você também encontrará exemplos passo a passo de distribuições de frequência e, além disso, poderá praticar com exercícios resolvidos.

O que é uma distribuição de frequência?

Nas estatísticas, a distribuição de frequência é uma tabela na qual os diferentes valores de uma amostra são agrupados em linhas e em cada coluna é exibido um tipo de frequência de cada valor. Portanto, a distribuição de frequência é usada para mostrar todos os tipos de frequências em um conjunto de dados.

Mais especificamente, uma distribuição de frequência inclui frequência absoluta, frequência absoluta cumulativa, frequência relativa e frequência relativa cumulativa.

Uma das características das distribuições de frequência é que elas são muito úteis para resumir uma amostra estatística de uma variável quantitativa e de uma variável qualitativa.

Como fazer uma distribuição de frequência

Para realizar uma distribuição de frequência, você deve seguir os seguintes passos:

1. Organize os dados em diferentes categorias e crie uma tabela em que cada linha corresponda a uma categoria.
2. Calcule a frequência absoluta de cada categoria na segunda coluna da tabela.
3. Calcule a frequência absoluta acumulada de cada categoria na terceira coluna da tabela.
4. Calcule a frequência relativa de cada categoria na quarta coluna da tabela.
5. Calcule a frequência relativa acumulada de cada categoria na quinta coluna da tabela.
6. Opcionalmente, podem ser adicionadas duas colunas nas quais a frequência relativa e a frequência relativa acumulada são calculadas como uma porcentagem, para isso basta multiplicar ambas as colunas por 100.

Exemplo de distribuição de frequência

Depois de vermos a definição de distribuição de frequência e a teoria de como ela é construída, nesta seção um exemplo é resolvido passo a passo.

• As notas obtidas na disciplina de estatística numa turma de 30 alunos são as seguintes. Construa uma distribuição de frequência do conjunto de dados.

Como todos os números só podem ser inteiros, é uma variável discreta. Portanto, não é necessário agrupar os dados em intervalos.

Então, para fazer uma distribuição de frequência, precisamos construir uma tabela na qual cada valor diferente será uma linha, e então precisamos encontrar a frequência absoluta de cada valor:

Observe que a soma de todas as frequências absolutas é igual ao número total de dados. Se esta regra não for respeitada, significa que você se esqueceu de fornecer algumas informações.

Agora que sabemos a frequência absoluta, precisamos calcular a frequência absoluta cumulativa. Para este cálculo temos duas opções: ou somamos a frequência absoluta do valor mais todas as frequências absolutas dos menores valores, ou pelo contrário, somamos a frequência absoluta do valor mais a frequência absoluta acumulada do valor anterior.

A frequência absoluta acumulada do último valor sempre corresponde ao número total de dados, você pode usar este truque para verificar se os cálculos estão corretos.

A seguir, precisamos determinar a frequência relativa, que é calculada dividindo a frequência absoluta pelo número total de pontos de dados (30):

Tenha em mente que a soma de todas as frequências relativas é sempre igual a 1, caso contrário significa que um determinado cálculo da distribuição de frequências está errado.

Finalmente, precisamos apenas extrair a frequência relativa cumulativa. Para isso, deve-se somar a frequência relativa do valor em questão mais todas as frequências relativas anteriores ou, o que dá no mesmo, a frequência relativa acumulada anterior:

Resumindo, a distribuição de frequência com todas as frequências dos dados do problema é a seguinte:

Distribuição de frequência para dados agrupados

Para fazer uma distribuição de frequência para dados agrupados em intervalos , a única diferença é que primeiro o conjunto de dados deve ser agrupado em intervalos diferentes, mas o resto dos cálculos são feitos da mesma forma que em uma distribuição de frequência sem agrupar os dados.

Como exemplo, um problema de construção de uma distribuição de frequência para dados agrupados é resolvido a seguir.

• A altura de 20 pessoas foi medida e os resultados abaixo foram obtidos. Crie uma distribuição de frequência separando os dados em intervalos.

Os dados desta amostra seguem uma distribuição contínua, pois os números podem ser decimais e, portanto, podem assumir qualquer valor. Portanto, faremos a distribuição de frequência agrupando os dados em intervalos.

Embora existam diversas regras matemáticas para a criação dos intervalos de uma amostra, neste caso criaremos simplesmente intervalos com largura de 10 décimos.

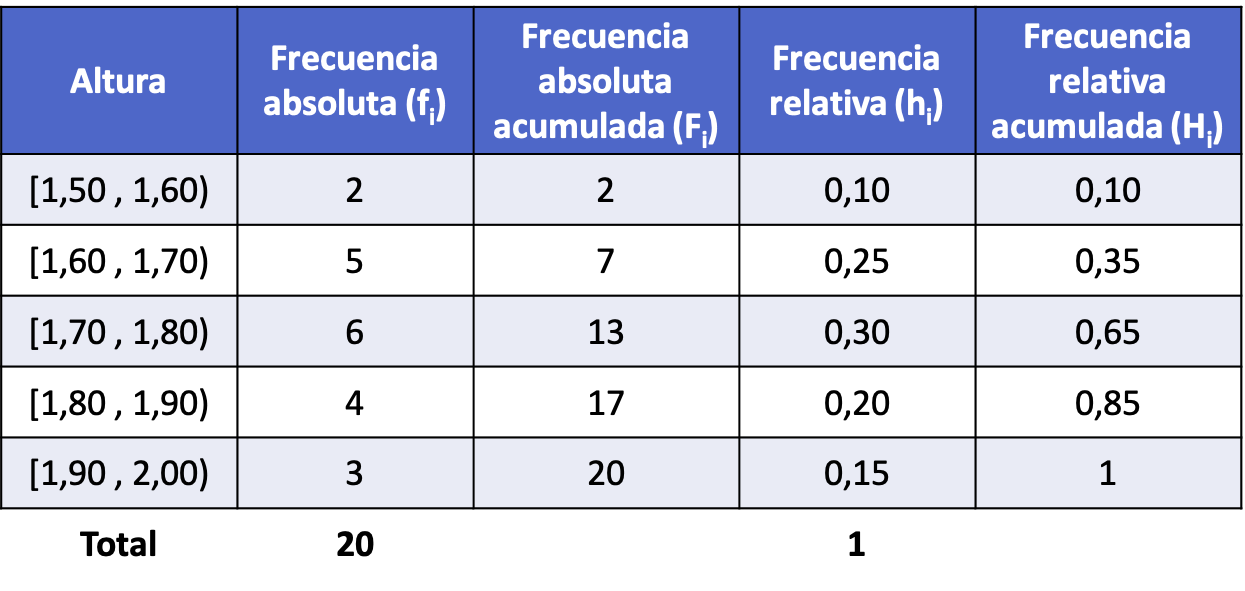
Assim, após calcular todos os tipos de frequência para cada intervalo (o procedimento é o mesmo do exemplo acima), a distribuição de frequência com os dados agrupados em intervalos fica da seguinte forma:

Exercícios resolvidos de distribuição de frequência

Exercício 1

Perguntamos a 20 pessoas quantas vezes elas vão ao cinema por mês e aqui estão os resultados:

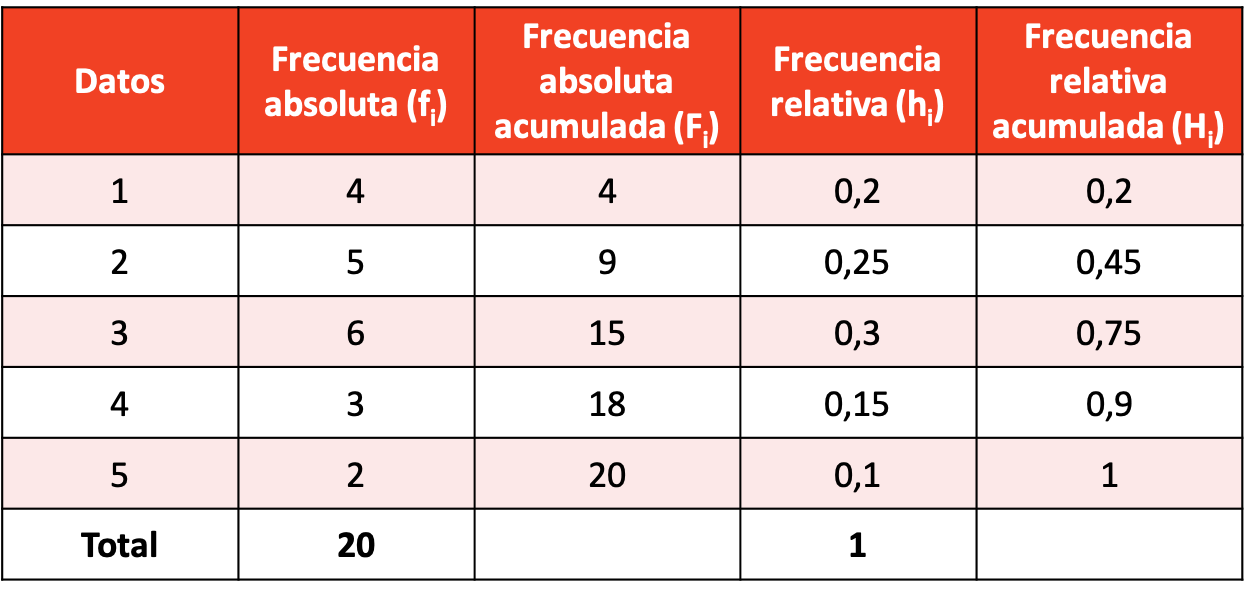
Faça uma distribuição de frequência com a amostra de dados resultante.

A distribuição de frequência com cálculos de todos os tipos de frequência é a seguinte:

Exercício 2

Gostaria de realizar um estudo estatístico sobre o peso dos trabalhadores numa empresa com 36 empregados. Aqui estão os pesos dos trabalhadores expressos em quilogramas:

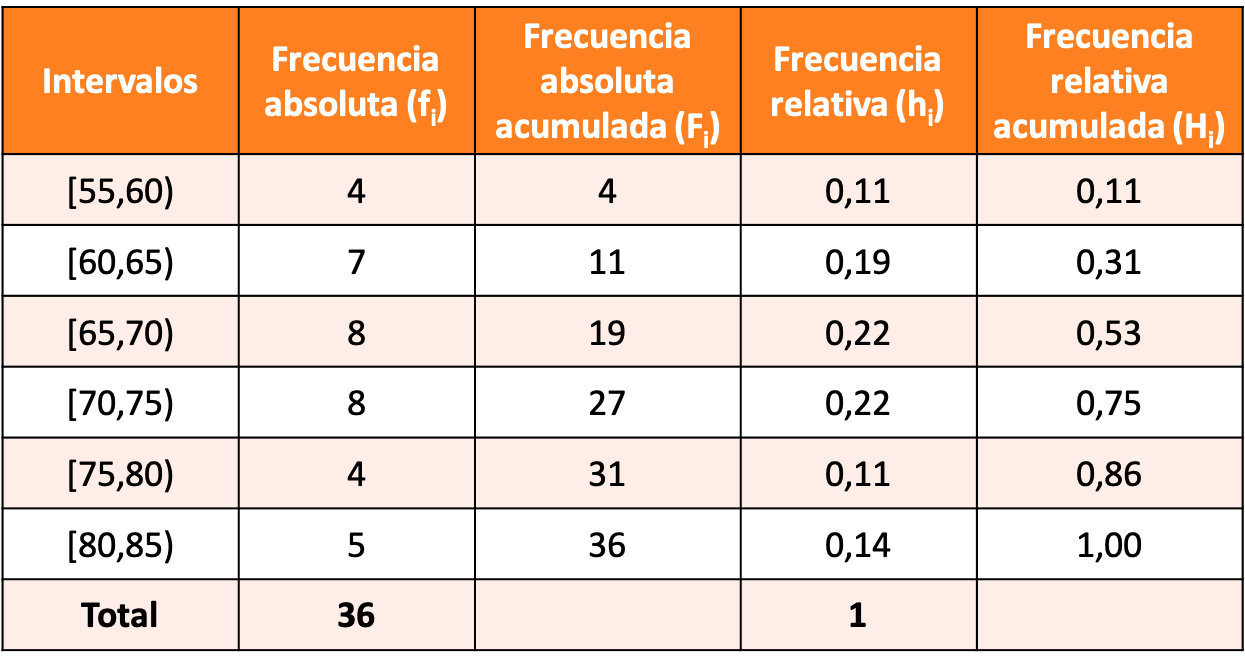
Construa uma distribuição de frequência com dados agrupados fazendo intervalos de 5 unidades e sendo o primeiro intervalo [55,60).

A solução do exercício é a seguinte distribuição de frequência: