Como usar a função lm() em r para ajustar modelos lineares

A função lm() em R é usada para ajustar modelos de regressão linear.

Esta função usa a seguinte sintaxe básica:

lm(fórmula, dados,…)

Ouro:

• fórmula: A fórmula do modelo linear (por exemplo, y ~ x1 + x2)
• dados: o nome do bloco de dados que contém os dados

O exemplo a seguir mostra como usar esta função em R para fazer o seguinte:

• Ajustar um modelo de regressão
• Ver resumo de ajuste do modelo de regressão
• Visualizar gráficos de diagnóstico de modelo
• Trace o modelo de regressão ajustado
• Faça previsões usando o modelo de regressão

Ajuste o modelo de regressão

O código a seguir mostra como usar a função lm() para ajustar um modelo de regressão linear em R:

 #define data
df = data. frame (x=c(1, 3, 3, 4, 5, 5, 6, 8, 9, 12),
                y=c(12, 14, 14, 13, 17, 19, 22, 26, 24, 22))

#fit linear regression model using 'x' as predictor and 'y' as response variable
model <- lm(y ~ x, data=df)

Mostrar resumo do modelo de regressão

Podemos então usar a função summary() para exibir o resumo do ajuste do modelo de regressão:

 #view summary of regression model
summary(model)

Call:
lm(formula = y ~ x, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4793 -0.9772 -0.4772 1.4388 4.6328 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 11.1432 1.9104 5.833 0.00039 ***
x 1.2780 0.2984 4.284 0.00267 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.929 on 8 degrees of freedom
Multiple R-squared: 0.6964, Adjusted R-squared: 0.6584 
F-statistic: 18.35 on 1 and 8 DF, p-value: 0.002675

Veja como interpretar os valores mais importantes do modelo:

• Estatística F = 18,35, valor p correspondente = 0,002675. Como esse valor de p é inferior a 0,05, o modelo como um todo é estatisticamente significativo.
• Múltiplo R ao quadrado = 0,6964. Isso nos diz que 69,64% da variação na variável resposta, y, pode ser explicada pela variável preditora, x.
• Coeficiente estimado de x : 1,2780. Isso nos diz que cada aumento unitário adicional em x está associado a um aumento médio de 1,2780 em y.

Podemos então usar as estimativas dos coeficientes da saída para escrever a equação de regressão estimada:

y = 11,1432 + 1,2780*(x)

Bônus : você pode encontrar um guia completo para interpretar cada valor da saída da regressão em R aqui .

Visualizar gráficos de diagnóstico de modelo

Podemos então usar a função plot() para traçar os gráficos de diagnóstico do modelo de regressão:

 #create diagnostic plots
plot(model) 

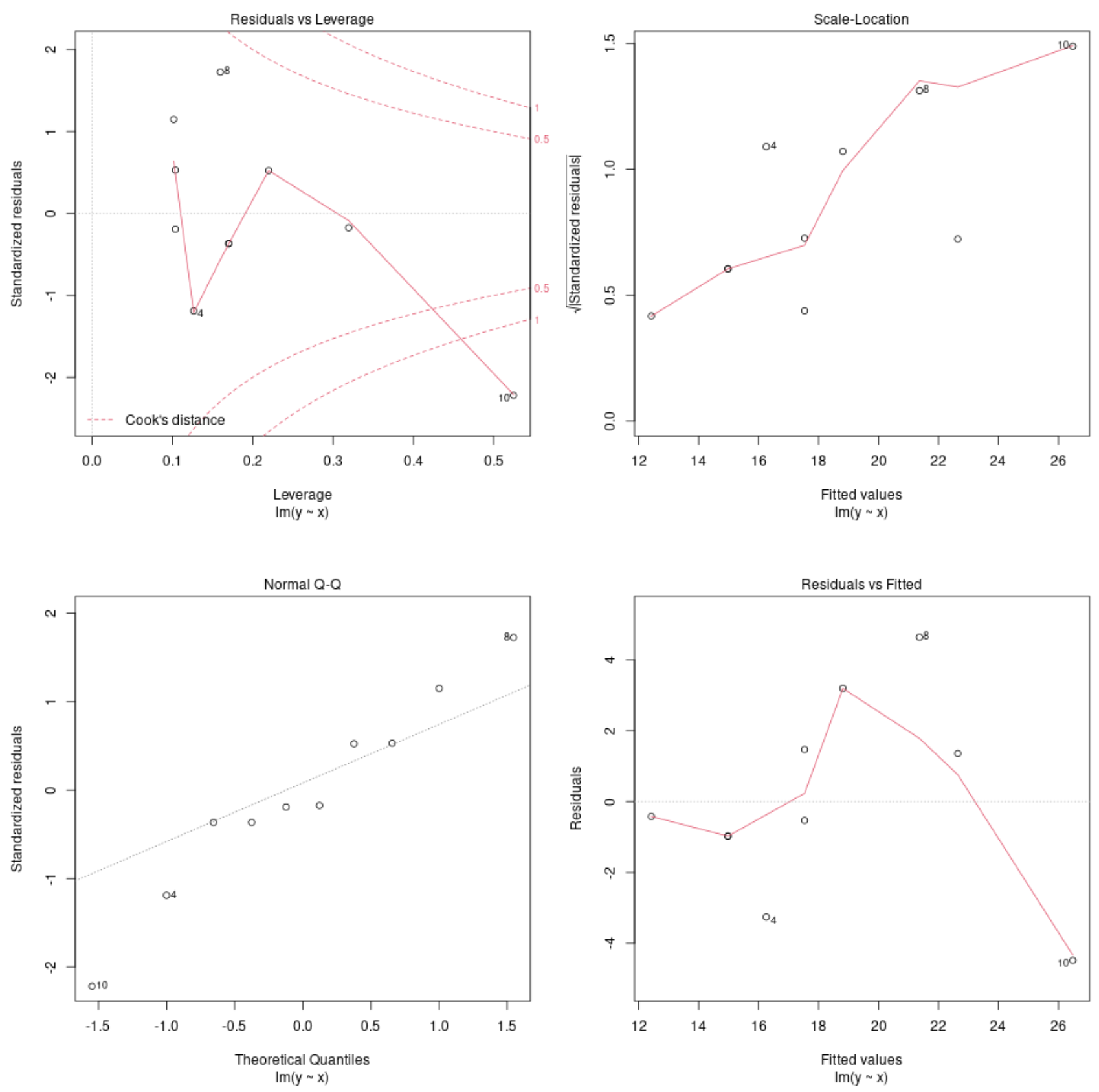
Esses gráficos nos permitem analisar os resíduos do modelo de regressão para determinar se o modelo é apropriado para uso nos dados.

Consulte este tutorial para obter uma explicação completa de como interpretar os gráficos de diagnóstico de um modelo em R.

Trace o modelo de regressão ajustado

Podemos usar a função abline() para traçar o modelo de regressão ajustado:

 #create scatterplot of raw data
plot(df$x, df$y, col=' red ', main=' Summary of Regression Model ', xlab=' x ', ylab=' y ')

#add fitted regression line
abline(model)

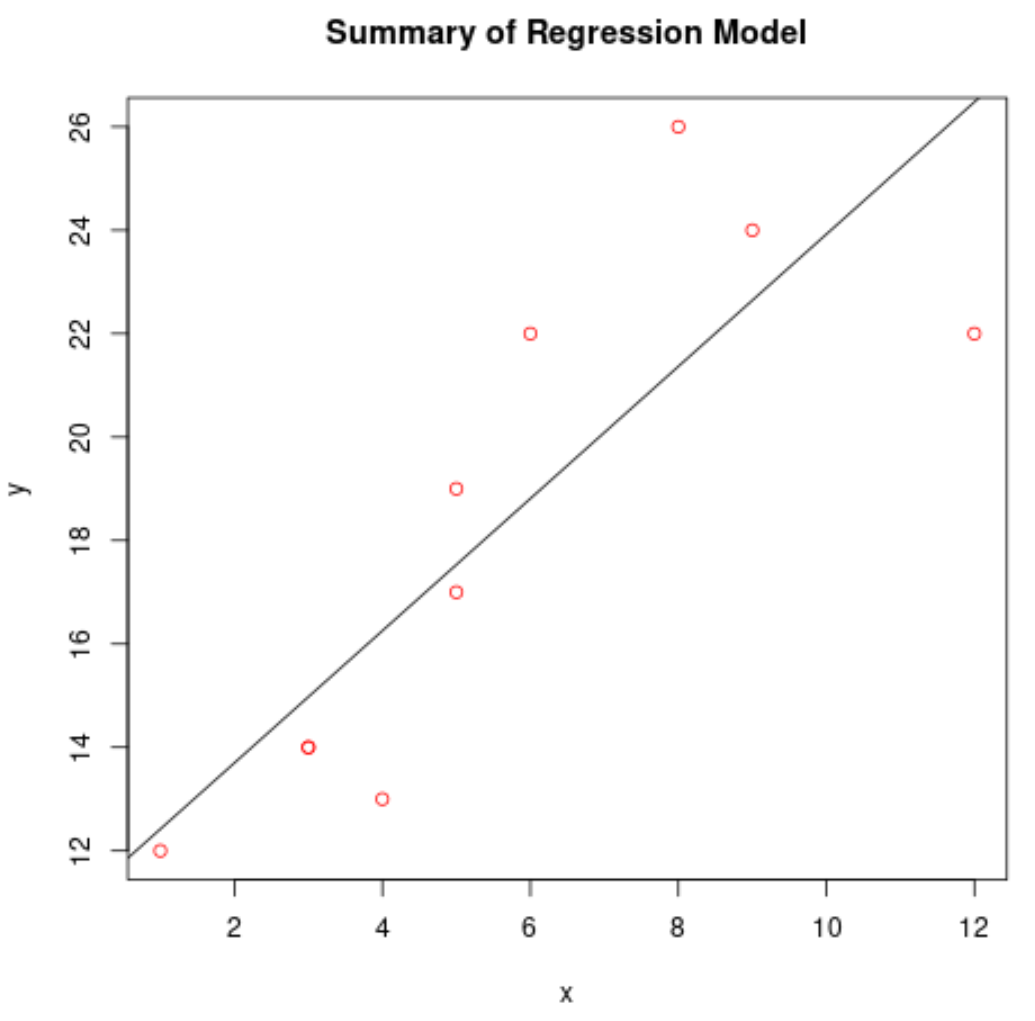
Use o modelo de regressão para fazer previsões

Podemos usar a função predizer() para prever o valor da resposta para uma nova observação:

 #define new observation
new <- data. frame (x=c(5))

#use the fitted model to predict the value for the new observation
predict(model, newdata = new)

      1 
17.5332

O modelo prevê que esta nova observação terá um valor de resposta de 17,5332 .

Recursos adicionais

Como realizar regressão linear simples em R
Como realizar regressão linear múltipla em R
Como realizar a regressão stepwise em R