4 exemplos de uso de testes qui-quadrado na vida real
Nas estatísticas, existem dois tipos diferentes de testes de qui-quadrado:
1. Teste de ajuste do qui-quadrado – Usado para determinar se uma variável categórica segue ou não uma distribuição hipotética.
2. Teste de Independência do Qui Quadrado – Usado para determinar se existe ou não uma associação significativa entre duas variáveis categóricas.
Neste artigo, compartilhamos vários exemplos de como cada um desses tipos de testes qui-quadrado são usados em situações do mundo real.
Exemplo 1: Teste de adequação do qui-quadrado
Suponha que o dono de uma loja afirme que um número igual de clientes vem à sua loja todos os dias da semana.
Para testar esta hipótese, ele registra o número de clientes que entram na loja em uma determinada semana e descobre o seguinte:
- Segunda-feira: 50 clientes
- Terça-feira: 60 clientes
- Quarta-feira: 40 clientes
- Quinta-feira: 47 clientes
- Sexta-feira: 53 clientes
Ele pode usar um teste de adequação do qui-quadrado para determinar se a distribuição dos clientes que chegam todos os dias é consistente com sua hipótese de distribuição.
Usando a calculadora do teste de adequação do qui-quadrado , ele pode ver que o valor p do teste é 0,359 .
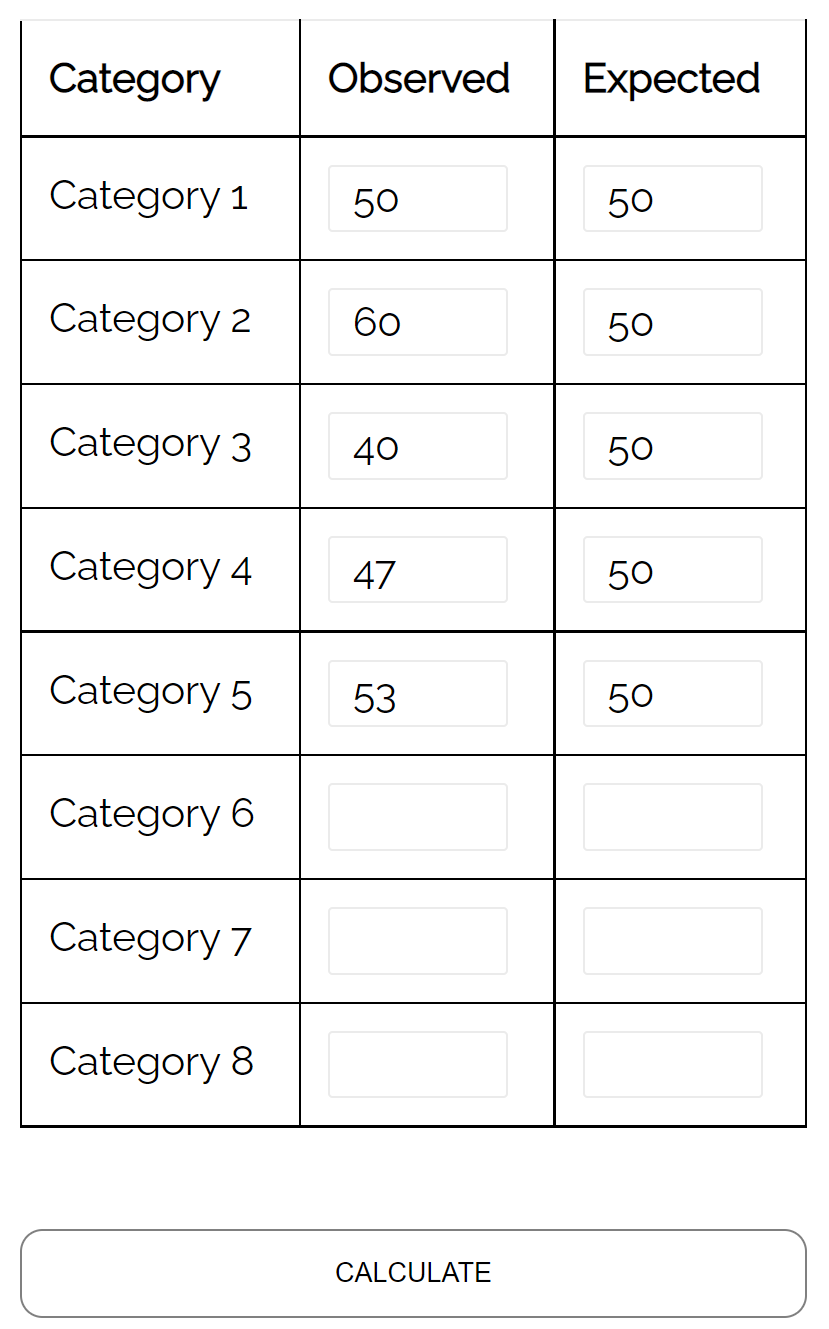

Como esse valor p não é inferior a 0,05, não há evidências suficientes para afirmar que a verdadeira distribuição dos clientes seja diferente daquela alegada pelo lojista.
Exemplo 2: Teste de adequação do qui-quadrado
Suponha que um biólogo afirme que um número igual de quatro espécies diferentes de cervos entra em uma determinada área arborizada de uma floresta a cada semana.
Para testar essa hipótese, ela registra o número de cada espécie de cervo que entra na área arborizada ao longo de uma semana:
- Espécie #1: 22
- Espécie #2: 20
- Espécie #3: 23
- Espécie #4: 35
Ela pode usar um teste de ajuste qui-quadrado para determinar se a distribuição das espécies de cervos que entram na área arborizada da floresta a cada semana é consistente com sua distribuição hipotética.
Usando a calculadora do teste qui-quadrado de qualidade de ajuste , ela pode ver que o valor p do teste é 0,137 .
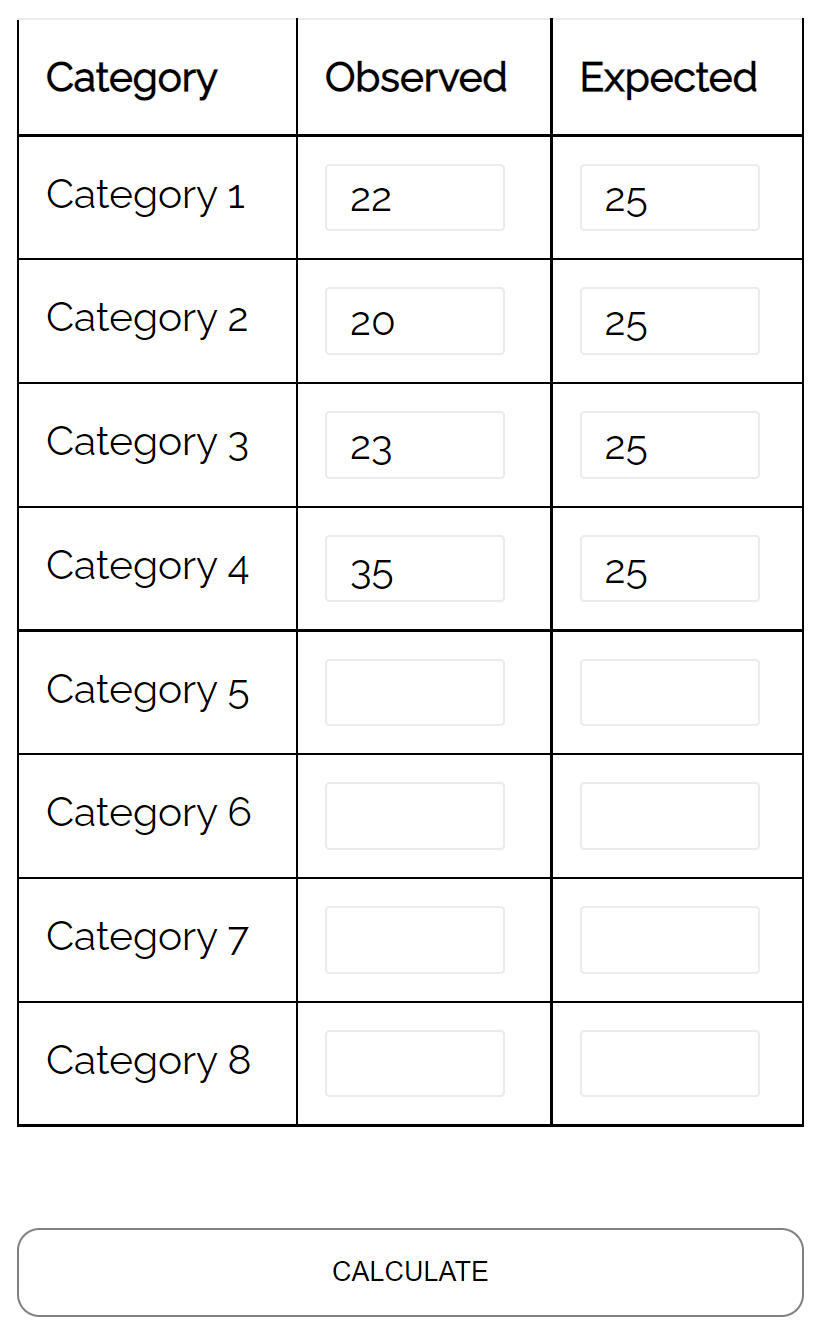
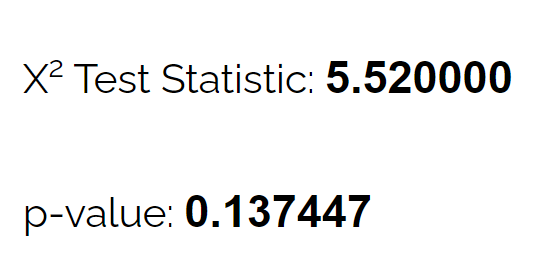
Dado que este valor p não é inferior a 0,05, não há provas suficientes para afirmar que a verdadeira distribuição dos cervos é diferente daquela alegada pelo biólogo.
Exemplo 3: Teste de independência qui-quadrado
Suponhamos que um decisor político numa determinada cidade queira saber se o género está ou não associado à preferência de um partido político.
Ele decide pegar uma amostra aleatória simples de 500 eleitores e perguntar-lhes sobre suas preferências partidárias. A tabela a seguir apresenta os resultados da pesquisa:
| Republicano | Democrata | Independente | Total | |
| Macho | 120 | 90 | 40 | 250 |
| Fêmea | 110 | 95 | 45 | 250 |
| Total | 230 | 185 | 85 | 500 |
Pode usar um teste de independência qui-quadrado para determinar se existe uma associação estatisticamente significativa entre as duas variáveis.
Usando a calculadora do teste de independência do qui-quadrado , ele pode ver que o valor p do teste é 0,649 .
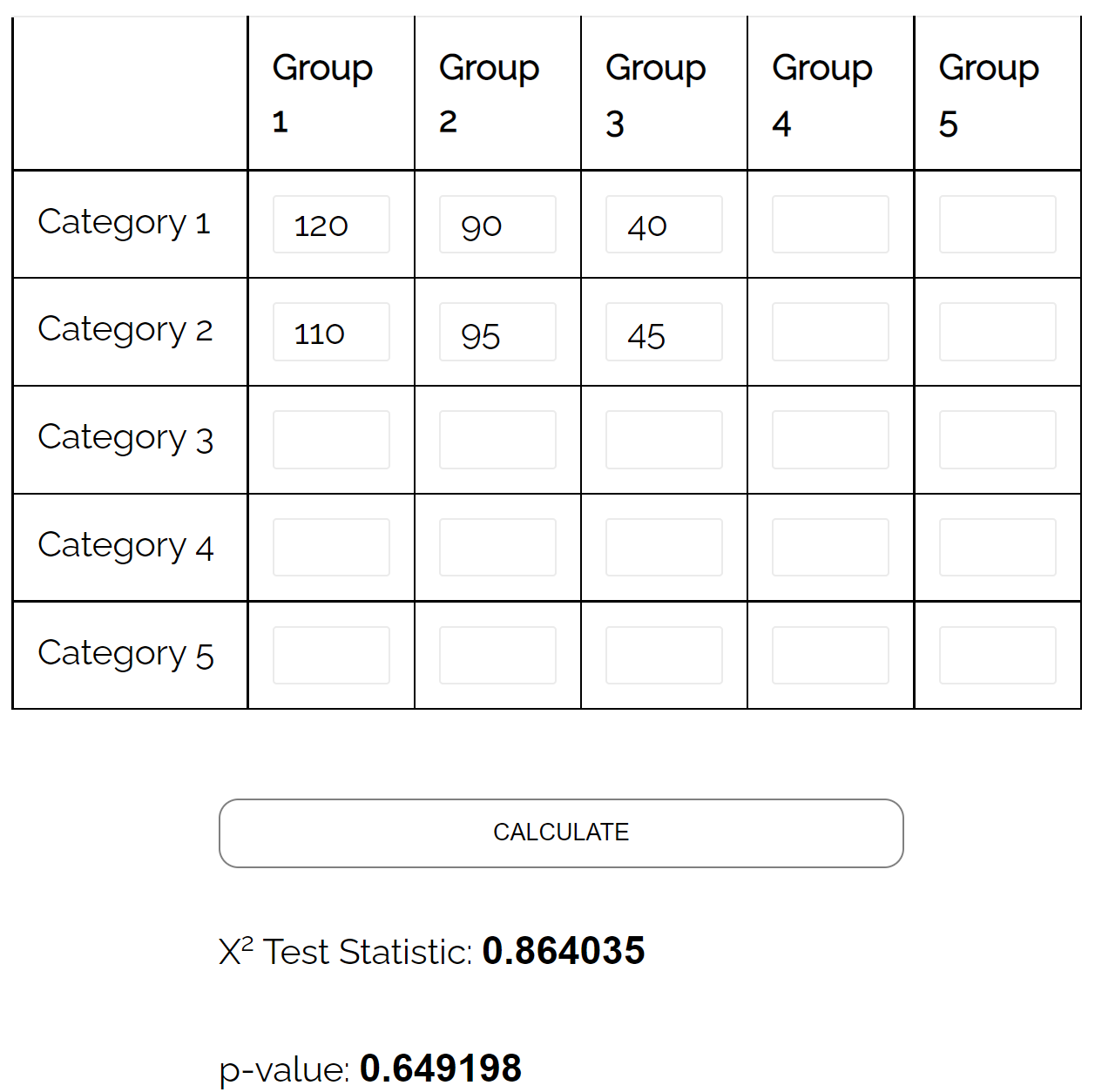
Dado que o valor p não é inferior a 0,05, não há provas suficientes para afirmar que existe uma associação entre género e preferência partidária.
Exemplo 4: Teste de independência qui-quadrado
Suponha que um pesquisador queira saber se o estado civil está ou não associado ao nível de escolaridade.
Ele decide pegar uma amostra aleatória simples de 300 indivíduos e obtém os seguintes resultados:
| Ensino médio | Bacharéis | Mestre ou superior | Total | |
| Casado | 20 | 100 | 35 | 155 |
| Bacharel | 50 | 80 | 15 | 145 |
| Total | 70 | 180 | 50 | 300 |
Pode usar um teste de independência qui-quadrado para determinar se existe uma associação estatisticamente significativa entre as duas variáveis.
Usando a calculadora do teste de independência do qui-quadrado , ele pode ver que o valor p do teste é 0,000011 .
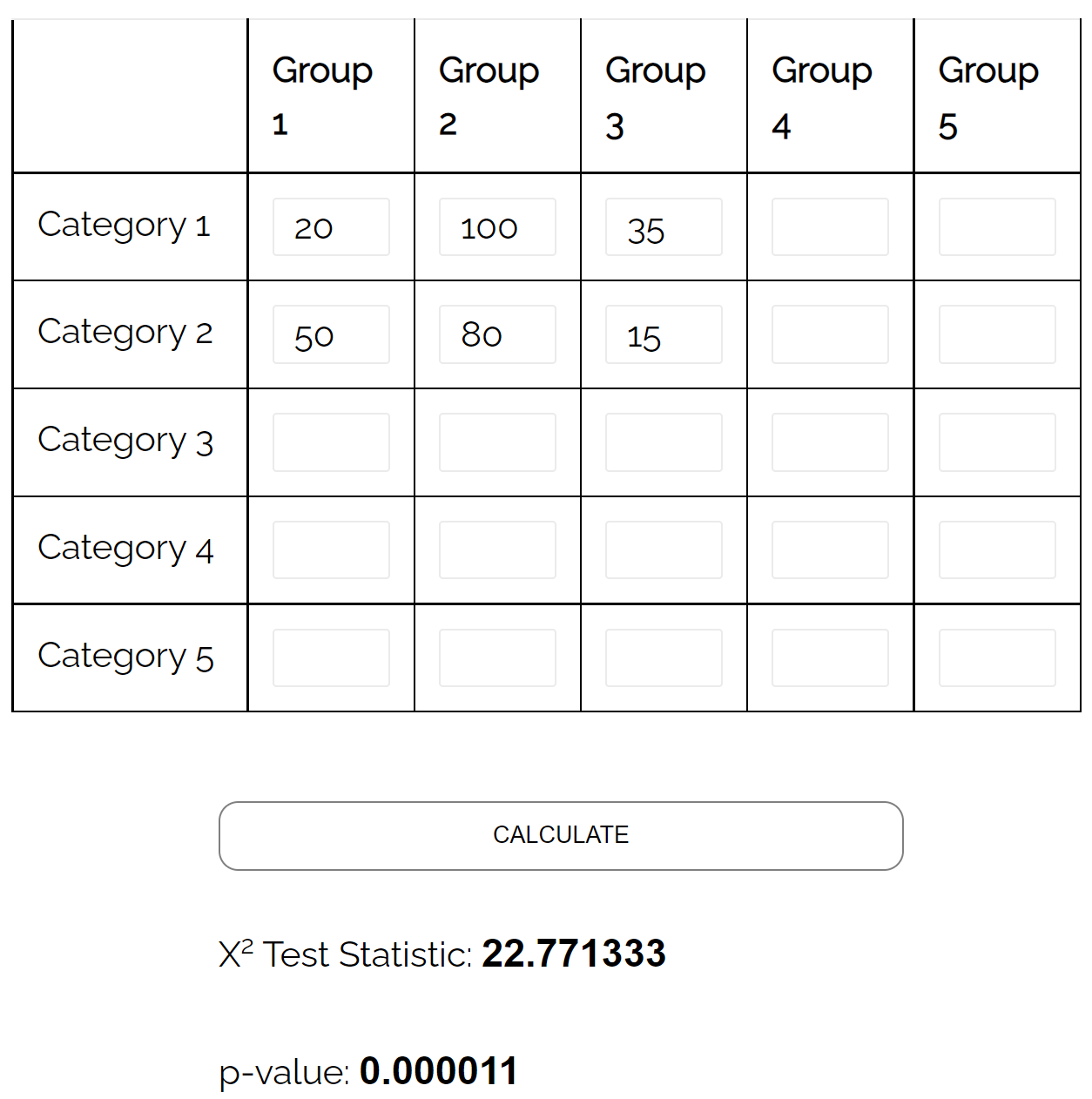
Como o valor p é inferior a 0,05, há evidências suficientes para afirmar que existe associação entre estado civil e nível de escolaridade.
Recursos adicionais
Os tutoriais a seguir fornecem uma introdução aos diferentes tipos de testes qui-quadrado:
Os tutoriais a seguir explicam a diferença entre testes qui-quadrado e outros testes estatísticos: