O que é multicolinearidade perfeita? (definição e exemplos)
Nas estatísticas, a multicolinearidade ocorre quando duas ou mais variáveis preditoras são altamente correlacionadas entre si, de modo que não fornecem informações únicas ou independentes no modelo de regressão.
Se o grau de correlação entre as variáveis for alto o suficiente, isso pode causar problemas no ajuste e na interpretação do modelo de regressão.
O caso mais extremo de multicolinearidade é denominado multicolinearidade perfeita . Isso ocorre quando duas ou mais variáveis preditoras têm um relacionamento linear exato entre si.
Por exemplo, suponha que temos o seguinte conjunto de dados:
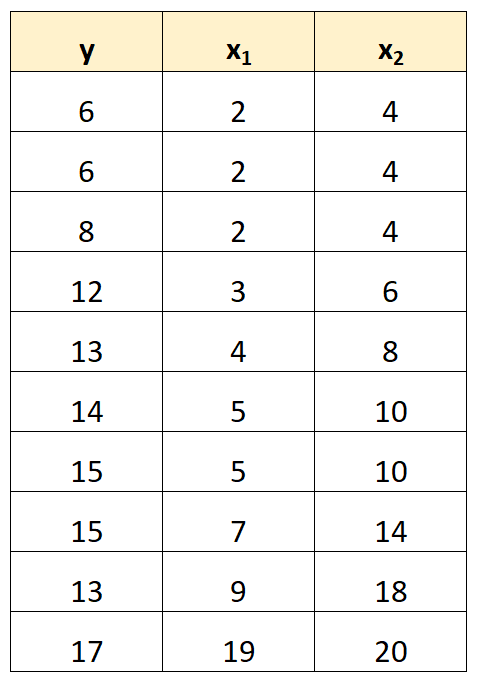
Observe que os valores da variável preditora x 2 são simplesmente os valores de x 1 multiplicados por 2.
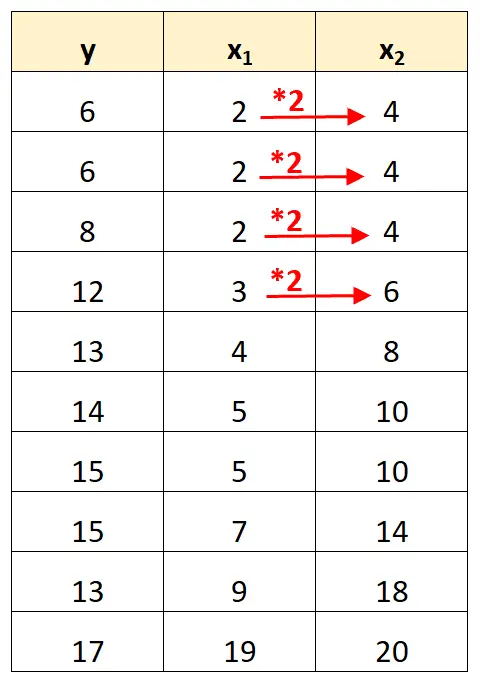
Este é um exemplo de multicolinearidade perfeita .
O problema da multicolinearidade perfeita
Quando a multicolinearidade perfeita está presente em um conjunto de dados, os mínimos quadrados ordinários são incapazes de produzir estimativas dos coeficientes de regressão.
Na verdade, não é possível estimar o efeito marginal de uma variável preditora (x 1 ) na variável de resposta (y) enquanto se mantém outra variável preditora (x 2 ) constante porque x 2 se move sempre exatamente quando x 1 se move.
Em suma, a multicolinearidade perfeita torna impossível estimar um valor para cada coeficiente num modelo de regressão.
Como lidar com multicolinearidade perfeita
A maneira mais simples de lidar com a multicolinearidade perfeita é remover uma das variáveis que possui uma relação linear exata com outra variável.
Por exemplo, em nosso conjunto de dados anterior, poderíamos simplesmente remover x 2 como variável preditora.
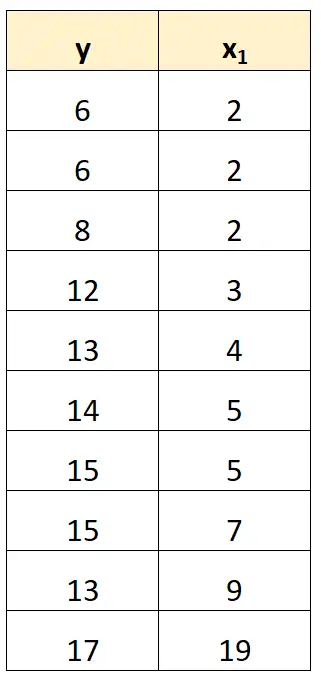
Ajustaríamos então um modelo de regressão usando x 1 como variável preditora e y como variável resposta.
Exemplos de multicolinearidade perfeita
Os exemplos a seguir mostram os três cenários mais comuns de multicolinearidade perfeita na prática.
1. Uma variável preditora é um múltiplo de outra
Digamos que queremos usar “altura em centímetros” e “altura em metros” para prever o peso de uma determinada espécie de golfinho.
Esta é a aparência do nosso conjunto de dados:
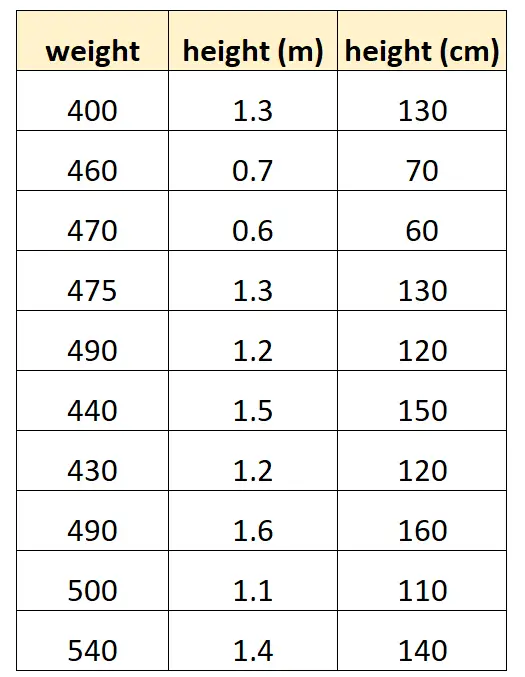
Observe que o valor de “altura em centímetros” é simplesmente igual a “altura em metros” multiplicado por 100. Este é um caso de multicolinearidade perfeita.
Se tentarmos ajustar um modelo de regressão linear múltipla em R usando este conjunto de dados, não seremos capazes de produzir uma estimativa de coeficiente para a variável preditora “metros”:
#define data df <- data. frame (weight=c(400, 460, 470, 475, 490, 440, 430, 490, 500, 540), m=c(1.3, .7, .6, 1.3, 1.2, 1.5, 1.2, 1.6, 1.1, 1.4), cm=c(130, 70, 60, 130, 120, 150, 120, 160, 110, 140)) #fit multiple linear regression model model <- lm(weight~m+cm, data=df) #view summary of model summary(model) Call: lm(formula = weight ~ m + cm, data = df) Residuals: Min 1Q Median 3Q Max -70,501 -25,501 5,183 19,499 68,590 Coefficients: (1 not defined because of singularities) Estimate Std. Error t value Pr(>|t|) (Intercept) 458,676 53,403 8,589 2.61e-05 *** m 9.096 43.473 0.209 0.839 cm NA NA NA NA --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 41.9 on 8 degrees of freedom Multiple R-squared: 0.005442, Adjusted R-squared: -0.1189 F-statistic: 0.04378 on 1 and 8 DF, p-value: 0.8395
2. Uma variável preditora é uma versão transformada de outra
Digamos que queremos usar “pontos” e “pontos em escala” para prever a classificação dos jogadores de basquete.
Suponha que a variável “pontos escalados” seja calculada como:
Pontos em escala = (pontos – μ pontos ) / σ pontos
Esta é a aparência do nosso conjunto de dados:
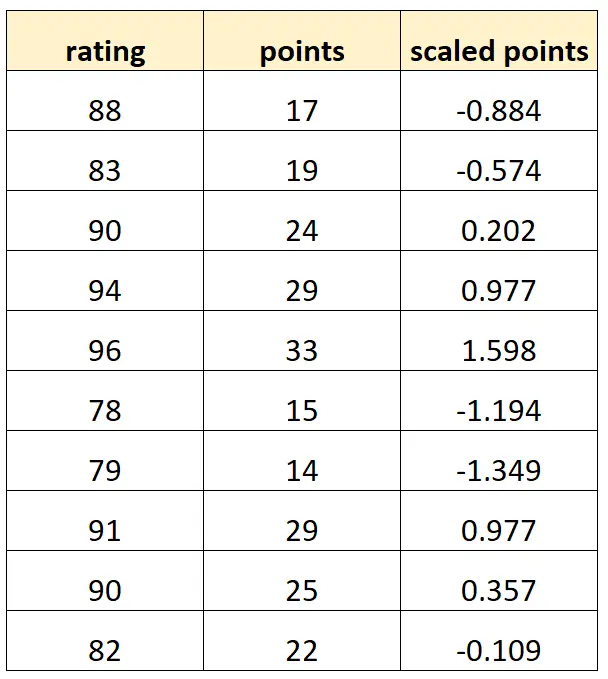
Observe que cada valor de “pontos em escala” é simplesmente uma versão padronizada de “pontos”. Este é um caso de multicolinearidade perfeita.
Se tentarmos ajustar um modelo de regressão linear múltipla em R usando este conjunto de dados, não seremos capazes de produzir uma estimativa de coeficiente para a variável preditora “pontos escalonados”:
#define data df <- data. frame (rating=c(88, 83, 90, 94, 96, 78, 79, 91, 90, 82), pts=c(17, 19, 24, 29, 33, 15, 14, 29, 25, 22)) df$scaled_pts <- (df$pts - mean(df$pts)) / sd(df$pts) #fit multiple linear regression model model <- lm(rating~pts+scaled_pts, data=df) #view summary of model summary(model) Call: lm(formula = rating ~ pts + scaled_pts, data = df) Residuals: Min 1Q Median 3Q Max -4.4932 -1.3941 -0.2935 1.3055 5.8412 Coefficients: (1 not defined because of singularities) Estimate Std. Error t value Pr(>|t|) (Intercept) 67.4218 3.5896 18.783 6.67e-08 *** pts 0.8669 0.1527 5.678 0.000466 *** scaled_pts NA NA NA NA --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 2.953 on 8 degrees of freedom Multiple R-squared: 0.8012, Adjusted R-squared: 0.7763 F-statistic: 32.23 on 1 and 8 DF, p-value: 0.0004663
3. A armadilha variável fictícia
Outro cenário em que pode ocorrer multicolinearidade perfeita é conhecido como armadilha de variável dummy . É quando queremos pegar uma variável categórica em um modelo de regressão e convertê-la em uma “variável fictícia” que assume os valores 0, 1, 2, etc.
Por exemplo, digamos que queremos usar as variáveis preditoras “idade” e “estado civil” para prever a renda:

Para usar o “estado civil” como variável preditora, devemos primeiro convertê-lo em uma variável dummy.
Para isso, podemos deixar “Solteiro” como valor base, já que isso acontece com mais frequência, e atribuir valores de 0 ou 1 para “Casado” e “Divórcio” da seguinte forma:

Um erro seria criar três novas variáveis fictícias da seguinte forma:

Neste caso, a variável “Solteiro” é uma combinação linear perfeita das variáveis “Casado” e “Divorciado”. Este é um exemplo de multicolinearidade perfeita.
Se tentarmos ajustar um modelo de regressão linear múltipla em R usando este conjunto de dados, não seremos capazes de produzir uma estimativa de coeficiente para cada variável preditora:
#define data df <- data. frame (income=c(45, 48, 54, 57, 65, 69, 78, 83, 98, 104, 107), age=c(23, 25, 24, 29, 38, 36, 40, 59, 56, 64, 53), single=c(1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0), married=c(0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1), divorced=c(0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0)) #fit multiple linear regression model model <- lm(income~age+single+married+divorced, data=df) #view summary of model summary(model) Call: lm(formula = income ~ age + single + married + divorced, data = df) Residuals: Min 1Q Median 3Q Max -9.7075 -5.0338 0.0453 3.3904 12.2454 Coefficients: (1 not defined because of singularities) Estimate Std. Error t value Pr(>|t|) (Intercept) 16.7559 17.7811 0.942 0.37739 age 1.4717 0.3544 4.152 0.00428 ** single -2.4797 9.4313 -0.263 0.80018 married NA NA NA NA divorced -8.3974 12.7714 -0.658 0.53187 --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 8.391 on 7 degrees of freedom Multiple R-squared: 0.9008, Adjusted R-squared: 0.8584 F-statistic: 21.2 on 3 and 7 DF, p-value: 0.0006865
Recursos adicionais
Um guia para multicolinearidade e VIF em regressão
Como calcular VIF em R
Como calcular VIF em Python
Como calcular VIF no Excel