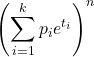Distribuição multinomial
Este artigo explica o que é uma distribuição multinomial em estatística. Assim, você encontrará a definição de distribuição multinomial, qual a sua fórmula, um exercício resolvido e quais são as propriedades desse tipo de distribuição de probabilidade. Além disso, você poderá calcular a probabilidade de uma distribuição multinomial com uma calculadora online.
O que é uma distribuição multinomial?
A distribuição multinomial (ou distribuição multinomial ) é uma distribuição de probabilidade que descreve a probabilidade de vários eventos mutuamente exclusivos ocorrerem um determinado número de vezes após várias tentativas.
Ou seja, se um experimento aleatório pode resultar em três ou mais eventos exclusivos e a probabilidade de cada evento ocorrer separadamente é conhecida, a distribuição multinomial é usada para calcular a probabilidade de que, quando vários experimentos são realizados, um certo número de eventos ocorra. vez, todas as vezes.
A distribuição multinomial é, portanto, uma generalização da distribuição binomial.
Fórmula de distribuição multinomial
Para calcular uma probabilidade de distribuição multinomial, deve-se primeiro determinar o quociente entre o fatorial do número total de dados e os fatoriais do número de ocorrências de cada evento, e o resultado é multiplicado pelo produto da probabilidade de cada evento. levado ao número de ocorrências do referido evento.
Em outras palavras, a fórmula para a distribuição multinomial é a seguinte:

Ouro:
-
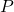
é a probabilidade da distribuição multinomial calculada.
-

é o número total de testes realizados.
-

é o número de vezes que o evento ocorre

.
-

é a probabilidade do evento ocorrer

.
👉 Você pode usar a calculadora abaixo para calcular a probabilidade de uma variável que segue a distribuição multinomial.
Exemplo de distribuição multinomial
Para finalizar a compreensão do conceito de distribuição multinomial, a seguir você resolveu um exemplo de cálculo da probabilidade de uma distribuição multinomial.
- Uma loja vende três produtos diferentes. Quando um cliente faz uma compra, a probabilidade de ser o produto A, o produto B ou o produto C é de 30%, 15% e 55% respectivamente. Encontre a probabilidade de que, quando a loja vendeu 8 unidades, 2 sejam do produto A, 1 do produto B e 5 do produto C.
O problema definido é regido por uma distribuição multinomial, sendo portanto necessário aplicar a fórmula para este tipo de distribuição de probabilidade:
![]()
Então substituímos os dados do problema na fórmula e realizamos o cálculo de probabilidade:
![]()
Portanto, a probabilidade de que o que a definição do problema diz aconteça é de 11,4%.
Calculadora de distribuição multinomial
Escreva o número de ocorrências de cada evento na primeira caixa e, na mesma ordem, a probabilidade de ocorrência de cada evento na segunda caixa. Em seguida, insira o número total de tentativas realizadas no último espaço em branco.
Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.
Propriedades da distribuição multinomial
A distribuição multinomial possui as seguintes características:
- Em uma distribuição multinomial, o valor esperado do número de vezes que o evento i ocorre ao executar n tentativas é igual ao número total de tentativas realizadas multiplicado pela probabilidade de ocorrência do evento.
![]()
- Em uma distribuição multinomial, a variância do evento i é calculada usando a seguinte expressão:
![]()
- Da mesma forma, a covariância entre dois eventos é equivalente ao produto do número total de tentativas multiplicado pela probabilidade de cada evento multiplicado por -1:
![]()
- A função geradora de momento para uma distribuição multinomial é: