Distribuição beta

By Dr. benjamim anderson Agosto 4, 2023 Probabilidade 0 Comments

Este artigo explica o que é distribuição beta e para que é usada. Da mesma forma, você poderá ver o gráfico da distribuição beta e as propriedades deste tipo de distribuição de probabilidade.

Qual é a distribuição beta?

A distribuição beta é uma distribuição de probabilidade definida no intervalo (0,1) e parametrizada por dois parâmetros positivos: α e β. Em outras palavras, os valores da distribuição beta dependem dos parâmetros α e β.

Portanto, a principal característica da distribuição beta é que sua forma pode ser controlada pelos parâmetros α e β. Além disso, a distribuição beta é usada para definir variáveis aleatórias cujo valor está entre 0 e 1.

Existem diversas notações para indicar que uma variável aleatória contínua é governada por uma distribuição beta, as mais comuns são:

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex]X\sim Beta(\alpha,\beta)\\[2ex]X\sim \beta_{\alpha,\beta}\end{array}$

Nas estatísticas, a distribuição beta tem aplicações muito variadas. Por exemplo, a distribuição beta é usada para estudar variações de porcentagens em diferentes amostras. Da mesma forma, no gerenciamento de projetos, a distribuição beta é usada para realizar análises Pert.

Gráfico de distribuição beta

Considerando a definição de distribuição beta, a função de densidade e a função de distribuição de probabilidade da distribuição beta são plotadas abaixo.

Abaixo você pode ver como o gráfico da função densidade da distribuição beta varia dependendo dos parâmetros α e β.

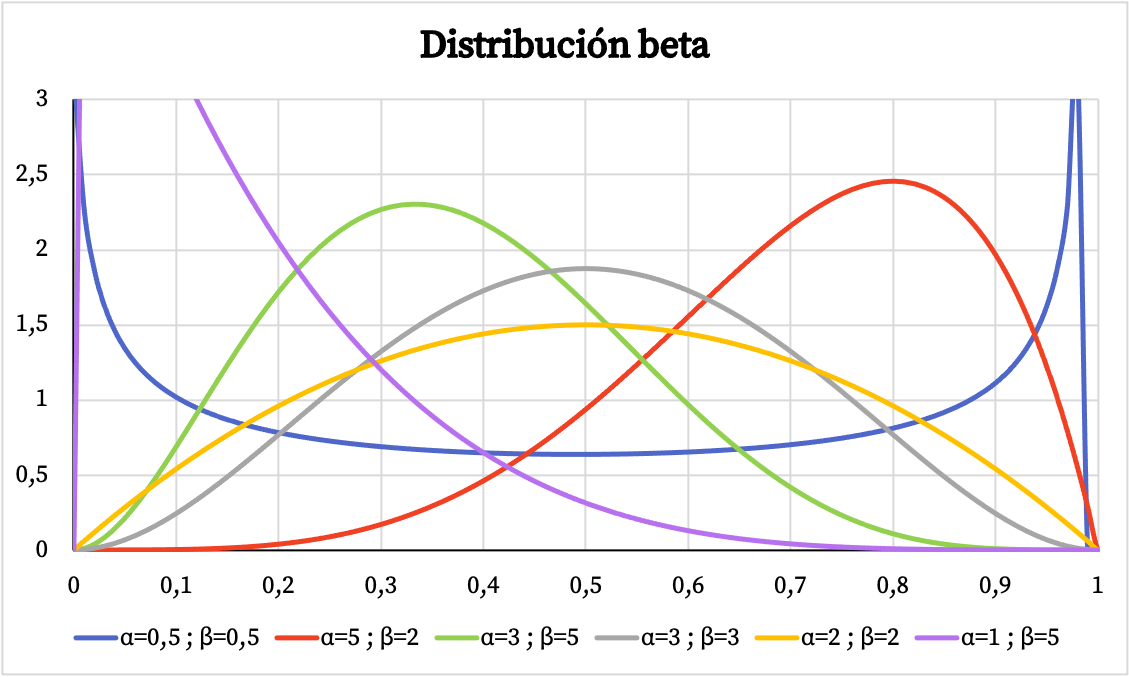
Da mesma forma, abaixo você pode ver a representação gráfica da probabilidade cumulativa da distribuição beta com base nos parâmetros α e β.

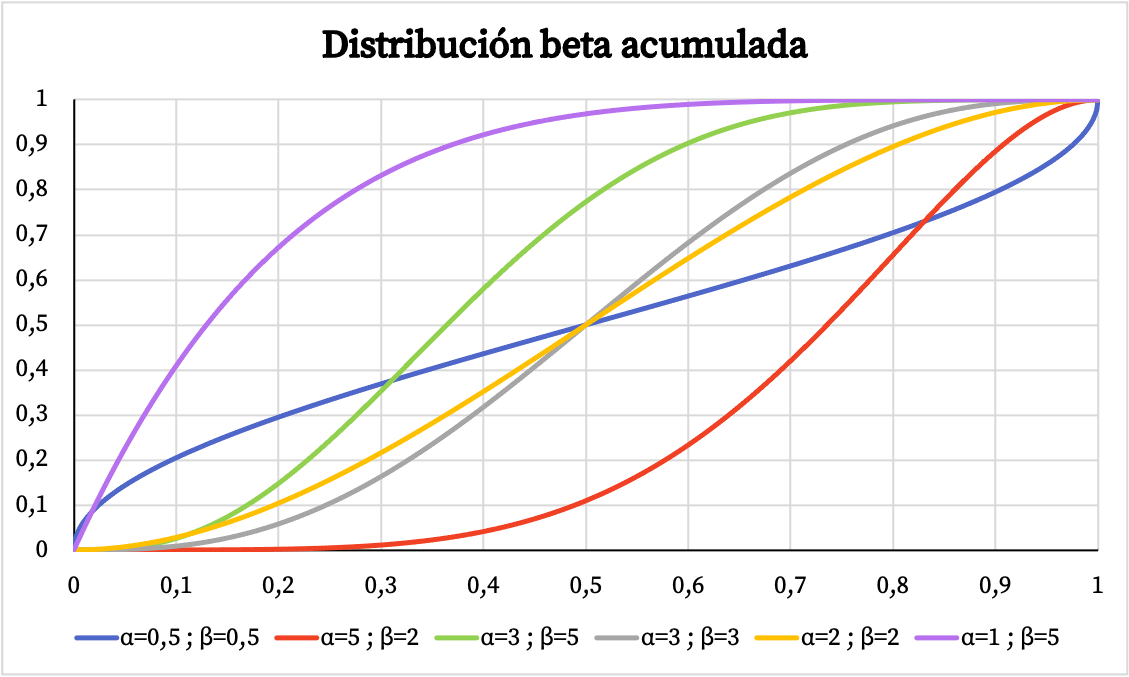
Características da distribuição beta

Nesta seção veremos quais são as características mais importantes da distribuição beta.

Os parâmetros α e β da distribuição beta são números reais e positivos.

$\begin{array}{c}\alpha >0\\[2ex] \beta >0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”44″ style=”vertical-align: 0px;”></p> </p> <ul> <li> O domínio da distribuição beta varia de 0 a 1, os dois extremos não estão incluídos.</li> </ul> <p class=$ $x\in (0,1)$

A média da distribuição beta é igual a alfa dividido pela soma alfa mais beta.

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] E[X]=\cfrac{\alpha}{\alpha+\beta}\end{array}$

A variância da distribuição beta pode ser calculada usando a seguinte fórmula:

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] Var(X)=\cfrac{\alpha\cdot \beta}{(\alpha+\beta+1)\cdot (\alpha+\beta)^2}\end{array}$

Para valores de alfa e beta maiores que 1, o modo de distribuição beta pode ser facilmente encontrado com a seguinte expressão:

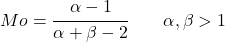
$Mo=\cfrac{\alpha-1}{\alpha+\beta-2}\qquad \alpha,\beta>1″ title=”Rendered by QuickLaTeX.com” height=”42″ width=”225″ style=”vertical-align: -16px;”></p> </p> <ul> <li> A função densidade da distribuição beta é a seguinte:</li> </ul> <p class=$ $\displaystyle P[X=x]=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}$

Onde B(α,β) é a função beta, que é definida como:

$\displaystyle B(\alpha,\beta)=\int_0^1x^{\alpha-1}(1-x)^{\beta-1}dx$

A função de probabilidade cumulativa da distribuição beta é:

$\displaystyle P[X\leq x]=\frac{B(x;\alpha,\beta)}{B(\alpha,\beta)}$

Onde B(x;α,β) é a função beta incompleta, definida como:

$\displaystyle B(x;\,a,b) = \int_0^x t^{a-1}\,(1-t)^{b-1}\,dt$

Se X é uma variável definida por uma distribuição beta, então 1-X é uma variável definida por uma distribuição beta cujos parâmetros alfa e beta são os parâmetros beta e alfa da distribuição beta original, respectivamente.

$X\sim B(\alpha,\beta) \ \color{orange}\bm{\longrightarrow}\color{black} \ 1-X\sim B(\beta,\alpha)$

Se os parâmetros alfa e beta da distribuição beta forem iguais a 1, então a distribuição será equivalente a uma distribuição uniforme dos parâmetros 0 e 1.

$X\sim B(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim U(0,1)$

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais

Qual é a distribuição beta?

Gráfico de distribuição beta

Características da distribuição beta

About Author

Dr. benjamim anderson

Add a Comment