Snedecor f distribuição

By Agosto 4, 2023 Probabilidade 0 Comments

Este artigo explica o que é a distribuição Snedecor F e para que é utilizada. Além disso, você poderá ver o gráfico de distribuição do Snedecor F e quais são suas propriedades estatísticas.

Qual é a distribuição Snedecor F?

A distribuição F de Snedecor , também chamada de distribuição F de Fisher-Snedecor ou simplesmente distribuição F , é uma distribuição de probabilidade contínua usada em inferência estatística, particularmente em análise de variância.

Uma das propriedades da distribuição Snedecor F é que ela é definida pelo valor de dois parâmetros reais, m e n , que indicam seus graus de liberdade. Assim, o símbolo para a distribuição Snedecor F é F m,n , onde m e n são os parâmetros que definem a distribuição.

F_{m,n}\qquad m,n>0″ title=”Rendered by QuickLaTeX.com” height=”18″ width=”139″ style=”vertical-align: -6px;”></p> </p> <p> Matematicamente, a distribuição Snedecor F é igual ao quociente entre uma distribuição qui-quadrado e seus graus de liberdade dividido pelo quociente entre outra distribuição qui-quadrado e seus graus de liberdade. Assim, a fórmula que define a distribuição Snedecor F é a seguinte: </p> </p> <p class=\left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}

A distribuição Fisher-Snedecor F deve seu nome ao estatístico inglês Ronald Fisher e ao estatístico americano George Snedecor.

Em estatística, a distribuição Fisher-Snedecor F tem diferentes aplicações. Por exemplo, a distribuição Fisher-Snedecor F é usada para comparar diferentes modelos de regressão linear, e esta distribuição de probabilidade é usada na análise de variância (ANOVA).

Diagrama de distribuição Snedecor F

Depois de vermos a definição da distribuição Snedecor F, o gráfico da sua função densidade e o gráfico da sua probabilidade cumulativa são mostrados abaixo.

No gráfico abaixo você pode ver vários exemplos de distribuições Snedecor F com diferentes graus de liberdade.

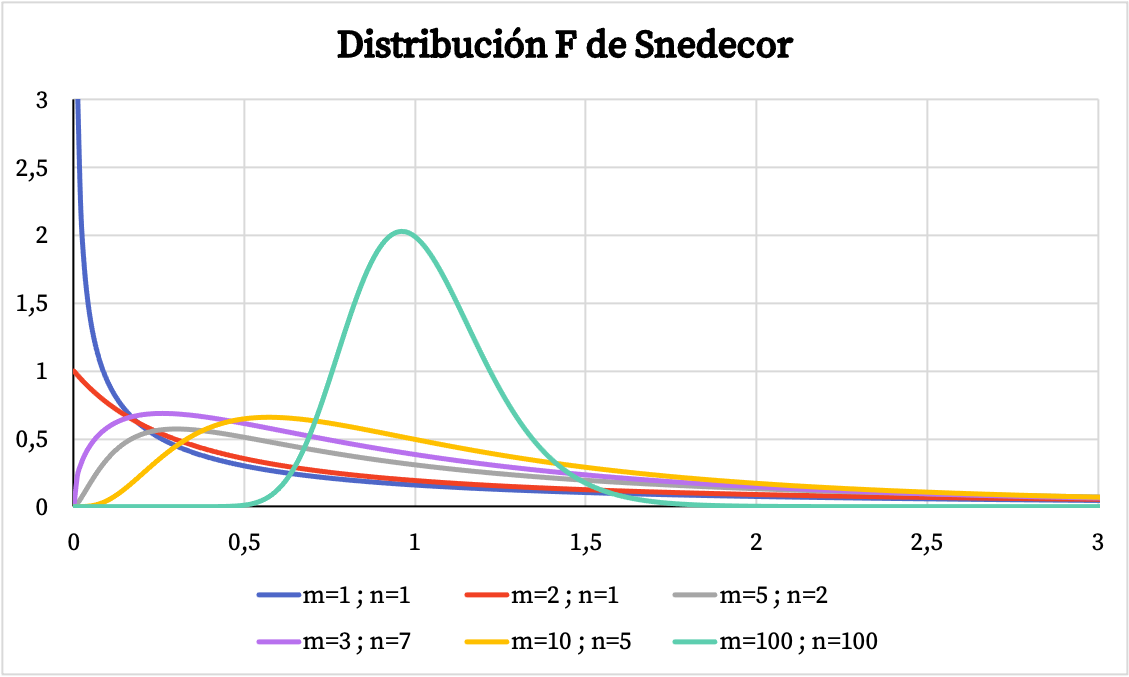
Gráfico de distribuição Snedecor F

Por outro lado, no gráfico abaixo você pode ver como o gráfico da função de probabilidade cumulativa da distribuição Snedecor F varia em função de seus valores característicos.

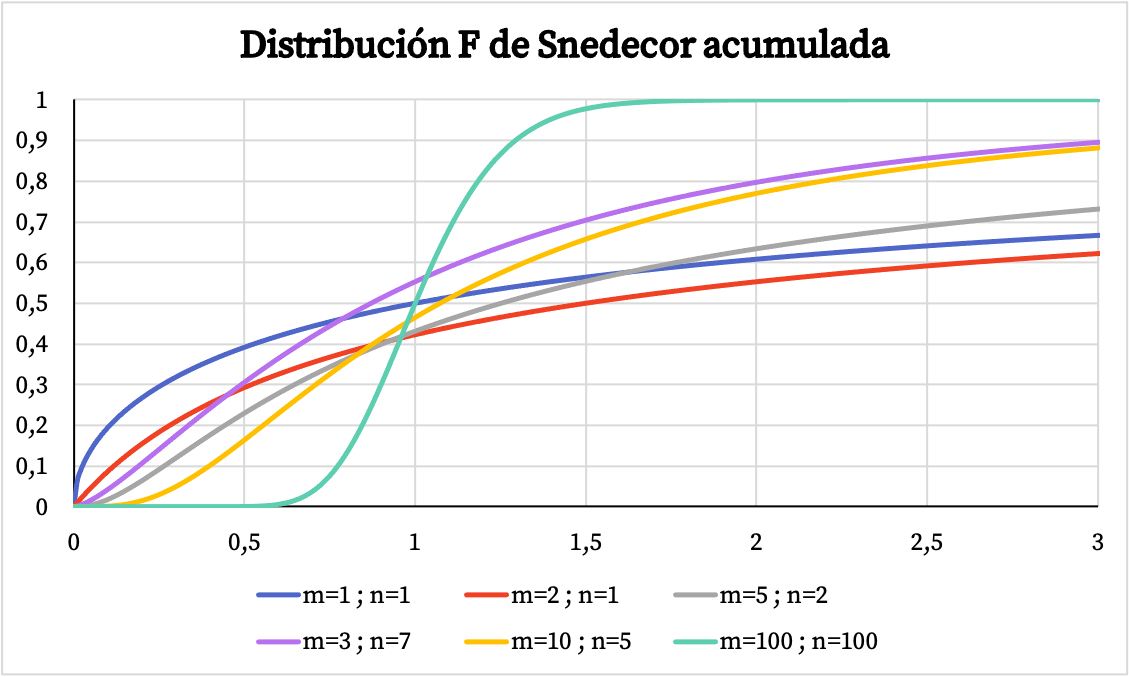
probabilidade cumulativa da distribuição Snedecor F

Características da distribuição Snedecor F

Finalmente, esta seção apresenta as características mais importantes da distribuição Snedecor F.

  • Os graus de liberdade da distribuição Snedecor F, m e n , são dois parâmetros que definem a forma da distribuição. Esses valores característicos da distribuição Snedecor F são números inteiros positivos.

\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”68″ style=”vertical-align: 0px;”></p> </p> <ul> <li> O domínio da distribuição Snedecor F consiste em todos os números reais maiores ou iguais a zero.</li> </ul> <p class=x\in [0,+\infty)

  • Para valores de n maiores que 2, a média da distribuição Snedecor F é igual a n na subtração de n menos 2.

\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”225″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Quando o parâmetro <em>n</em> é maior que 2, a variância da distribuição Snedecor F pode ser calculada aplicando a seguinte fórmula:</li> </ul> <p class=\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array} ” title=”Rendered by QuickLaTeX.com” height=”80″ width=”366″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Se o parâmetro <em>m</em> for maior que 2, a moda da distribuição Snedecor F pode ser calculada com a seguinte expressão:</li> </ul> <p class=Mo=\cfrac{m-2}{m}\cdot \cfrac{n}{n+2}\qquad \text{para }m>2″ title=”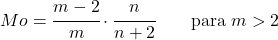Rendered by QuickLaTeX.com” height=”40″ width=”278″ style=”vertical-align: -14px;”></p> </p> <ul> <li> A fórmula para a função densidade da distribuição Snedecor F é a seguinte:</li> </ul> <p class=\displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}

  • Se uma variável segue uma distribuição Snedecor F com graus de liberdade m e n , então o inverso da referida variável segue uma distribuição Snedecor F com os mesmos graus de liberdade mas alterando a ordem dos seus valores.

X\sim F_{m,n} \ \color{orange}\bm{\longrightarrow}\color{\black} \ X^{-1}\sim F_{n,m}

  • A distribuição Student tem a seguinte relação com a distribuição Snedecor F:

X\sim t_n \ \color{orange}\bm{\longrightarrow}\color{\black} \ X^2\sim F_{1,n}

About Author

Dr. Benjamin Anderson
Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais

Add a Comment

O seu endereço de email não será publicado. Campos obrigatórios marcados com *