Distribuição normal padrão

Este artigo explica o que é a distribuição normal padrão e para que ela é usada. Você também encontrará as propriedades da distribuição normal padrão, a tabela com seus valores característicos e, além disso, um exercício resolvido.

Qual é a distribuição normal padrão?

A distribuição normal padrão , também chamada de distribuição normal unitária , é o caso mais simples de distribuição normal. Mais precisamente, a distribuição normal padrão é uma distribuição normal com valores de média e desvio padrão iguais a 0 e 1 respectivamente.

Portanto, a distribuição normal padrão é definida como N(0,1), onde o primeiro parâmetro é a média da distribuição e o segundo parâmetro é o seu desvio padrão (ou DP).

O gráfico da distribuição normal padrão é, portanto, o seguinte:

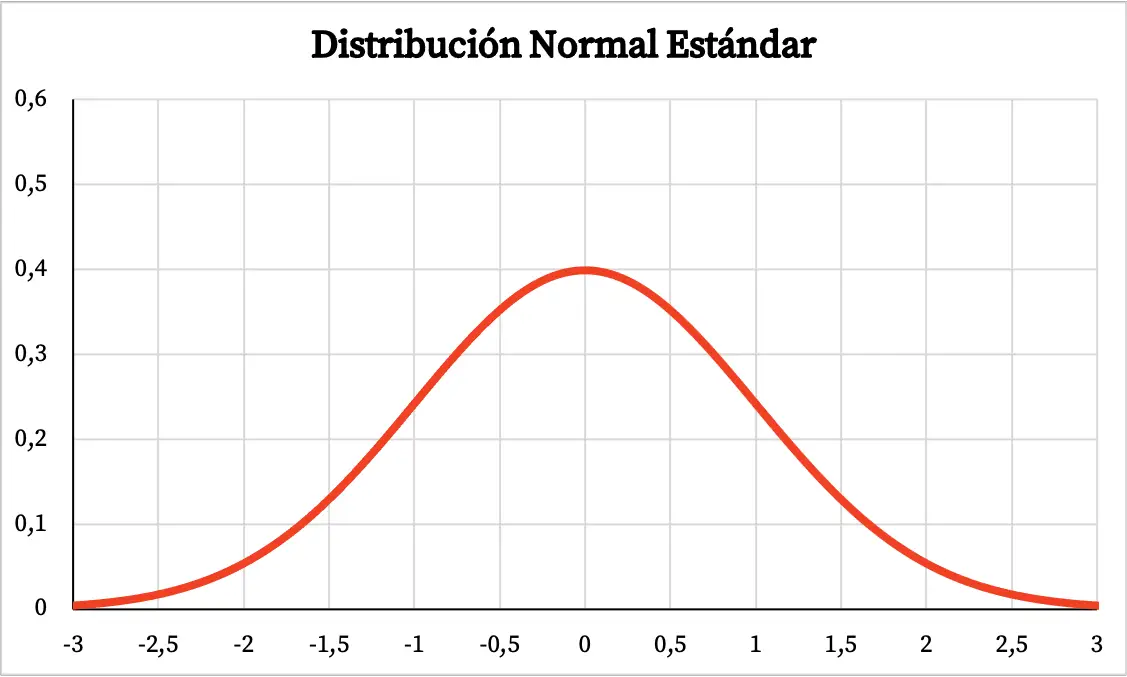
Fórmula para a distribuição normal padrão

Para transformar qualquer distribuição normal em uma distribuição normal padrão, deve-se subtrair a média da distribuição normal de todos os seus valores e depois dividir pelo desvio padrão da distribuição normal.

A fórmula para a distribuição normal padrão é, portanto, a seguinte:

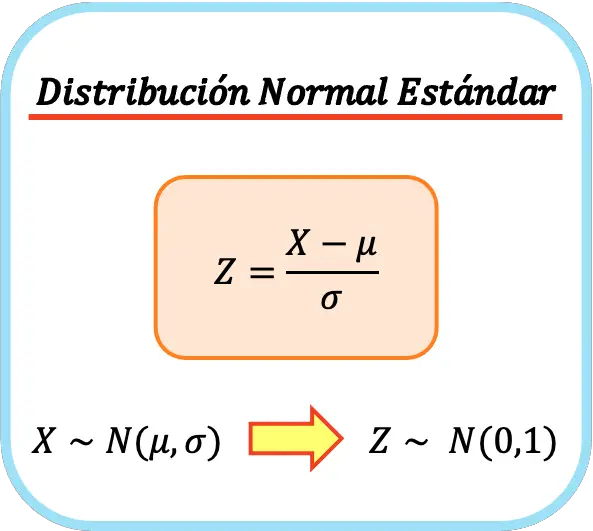
Desta forma, a média aritmética e o desvio padrão da nova variável serão 0 e 1 respectivamente, obteremos uma distribuição normal padrão. Este processo também é chamado de normalização univariada ou normalização univariada .

Tabela de distribuição normal padrão

A tabela de uma distribuição normal padrão é uma tabela que contém as probabilidades de um valor observado ser menor que um determinado valor da distribuição normal padrão.

Além disso, como a função de uma distribuição normal depende da sua média e desvio padrão, a tabela de distribuição normal padrão também é utilizada, por extensão, para determinar as probabilidades de qualquer distribuição normal. Para fazer isso, a distribuição normal é digitada em uma distribuição normal padrão e então observamos na tabela qual probabilidade corresponde a ela.

Portanto, os valores na tabela de distribuição normal padrão são os seguintes:

Exemplo de distribuição normal padrão

Agora que sabemos a definição de distribuição normal padrão e qual é sua fórmula, segue abaixo um exemplo concreto para entender bem o conceito.

• Uma variável aleatória contínua segue uma distribuição normal com média 45 e desvio padrão 15, qual a probabilidade de obter um valor menor ou igual a 58?

Para encontrar a probabilidade de uma distribuição normal, precisamos usar sua tabela de características, mas para fazer isso, primeiro precisamos fazer o processo de digitação para obter a distribuição normal padrão. Portanto, usamos a fórmula de distribuição normal padrão:

Então, subtraímos a média do valor da probabilidade e depois dividimos pelo desvio padrão

Depois de padronizarmos a variável, vamos para a tabela de probabilidade de distribuição normal padrão (veja acima) para ver a que probabilidade corresponde o valor de 0,87:

A probabilidade de obter um valor igual ou inferior a 58 é, portanto, de 80,78%.

Características da distribuição normal padrão

A distribuição normal padrão possui as seguintes características:

• A distribuição normal padrão é uma distribuição simétrica centrada em 0.
• Como uma distribuição normal, o gráfico de distribuição normal padrão tem formato de sino, com a maior parte da área do gráfico caindo em torno da média.
• Portanto, a média, a moda e a mediana de uma distribuição normal têm o mesmo valor, que é 0.
• A distribuição normal padrão tem um máximo em z=0.
• Da mesma forma, a distribuição normal padrão tem dois pontos de inflexão, em z=-1 e z=+1.
• De acordo com a regra prática, sabemos que 68% dos valores se enquadram em uma distribuição normal padrão entre +1 e -1, 95% dos valores entre +2 e -2 e 99,7% dos valores entre + 3 e – 3.