Distribuição gama

Este artigo explica o que é a distribuição gama e para que ela é usada. Assim, você encontrará a definição da distribuição gama, suas propriedades e como é sua representação gráfica.

Qual é a distribuição gama?

A distribuição gama é uma distribuição de probabilidade contínua definida por dois parâmetros característicos, α e λ. Em outras palavras, a distribuição gama depende do valor de seus dois parâmetros: α é o parâmetro de forma e λ é o parâmetro de escala.

O símbolo da distribuição gama é a letra grega maiúscula Γ. Portanto, se uma variável aleatória segue uma distribuição gama, ela é escrita da seguinte forma:

A distribuição gama também pode ser parametrizada usando o parâmetro de forma k = α e o parâmetro de escala inversa θ = 1/λ. Em todos os casos, os dois parâmetros que definem a distribuição gama são números reais positivos.

Normalmente, a distribuição gama é usada para modelar conjuntos de dados distorcidos à direita, de modo que haja uma maior concentração de dados no lado esquerdo do gráfico. Por exemplo, a distribuição gama é usada para modelar a confiabilidade de componentes elétricos.

Diagrama de distribuição gama

O gráfico da distribuição gama depende dos valores de seus parâmetros característicos. Abaixo você pode ver como a função de densidade da distribuição gama varia dependendo do parâmetro de forma e do parâmetro de escala.

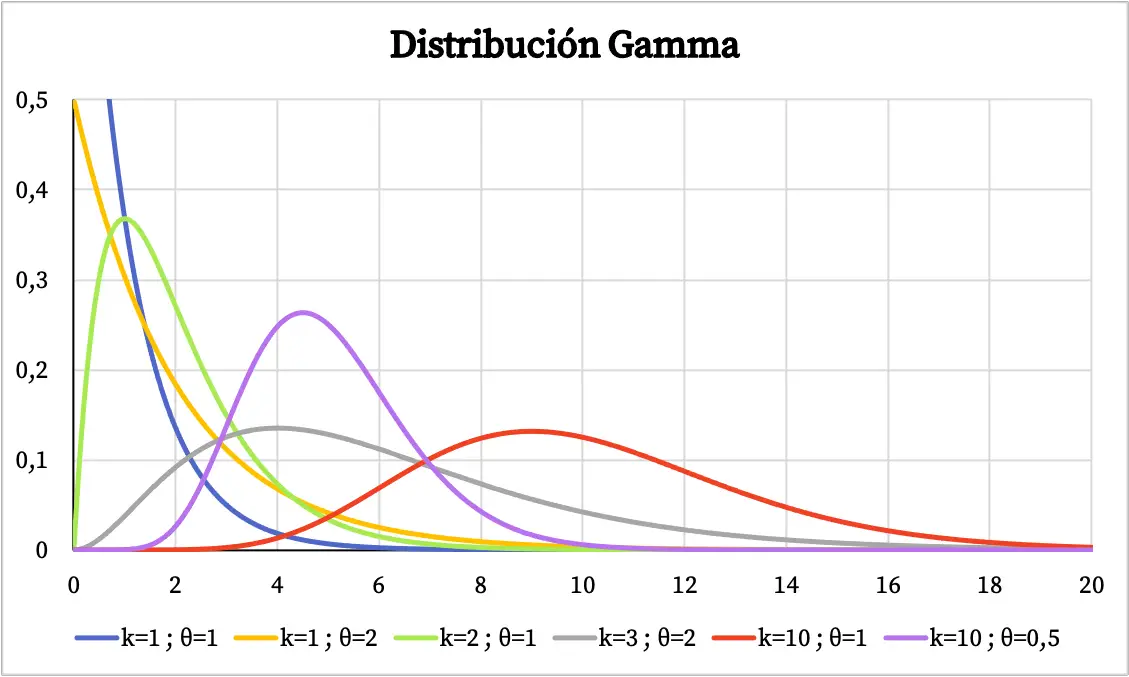
Por outro lado, você pode ver o gráfico da função de probabilidade cumulativa da distribuição gama abaixo:

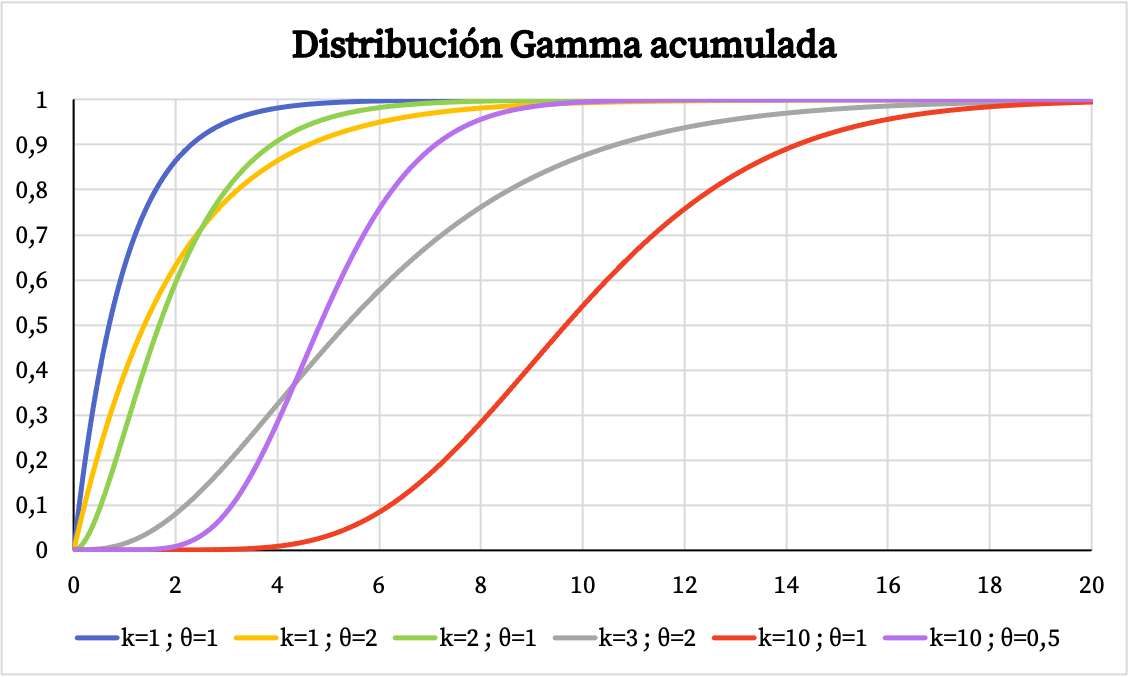
Características da distribuição gama

Veremos então quais são as características da distribuição gama.

• O gráfico da distribuição gama é inteiramente definido por seus dois parâmetros característicos: α é o parâmetro de forma e λ é o parâmetro de escala.

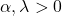
• A média da distribuição gama é igual à razão entre o parâmetro de forma e o parâmetro de escala, ou seja, α/λ.

• A variância da distribuição gama é equivalente ao parâmetro de forma dividido pelo quadrado do parâmetro de escala.

• Para valores de α menores que 1, a moda é 0. Mas se α for igual ou maior que 1, a moda da distribuição gama pode ser calculada com a seguinte fórmula:

• A fórmula para a função densidade da distribuição gama é:

Onde Γ é a função gama, que é definida como:

• A fórmula para a distribuição cumulativa de uma variável aleatória definida por uma distribuição gama é a seguinte:

• Se o parâmetro de forma α for igual a 1, então a distribuição gama é equivalente a uma distribuição exponencial com o mesmo parâmetro de escala λ.

• Quando o parâmetro de escala λ é uma média, então a distribuição gama é um caso especial da distribuição qui-quadrado .