Como transformar dados em python (log, raiz quadrada, raiz cúbica)
Muitos testes estatísticos assumem que os conjuntos de dados são normalmente distribuídos. No entanto, muitas vezes este não é o caso na prática.
Uma maneira de resolver esse problema é transformar a distribuição de valores em um conjunto de dados usando uma das três transformações:
1. Transformação de log: transforme a variável de resposta de y em log(y) .
2. Transformação de raiz quadrada: Transforme a variável de resposta de y em √y .
3. Transformação da raiz cúbica: transforme a variável de resposta de y em y 1/3 .
Ao realizar essas transformações, o conjunto de dados geralmente se torna distribuído de forma mais normal.
Os exemplos a seguir mostram como realizar essas transformações em Python.
Transformação de log em Python
O código a seguir mostra como realizar uma transformação logarítmica em uma variável e criar gráficos lado a lado para exibir a distribuição original e a distribuição dos dados transformada em logaritmo:
import numpy as np import matplotlib. pyplot as plt #make this example reproducible n.p. random . seeds (0) #create beta distributed random variable with 200 values data = np. random . beta (a= 4 , b= 15 , size= 300 ) #create log-transformed data data_log = np. log (data) #define grid of plots fig, axs = plt. subplots (nrows= 1 , ncols= 2 ) #create histograms axs[0]. hist (data, edgecolor=' black ') axs[1]. hist (data_log, edgecolor=' black ') #add title to each histogram axs[0]. set_title (' Original Data ') axs[1].set_title(' Log-Transformed Data ')
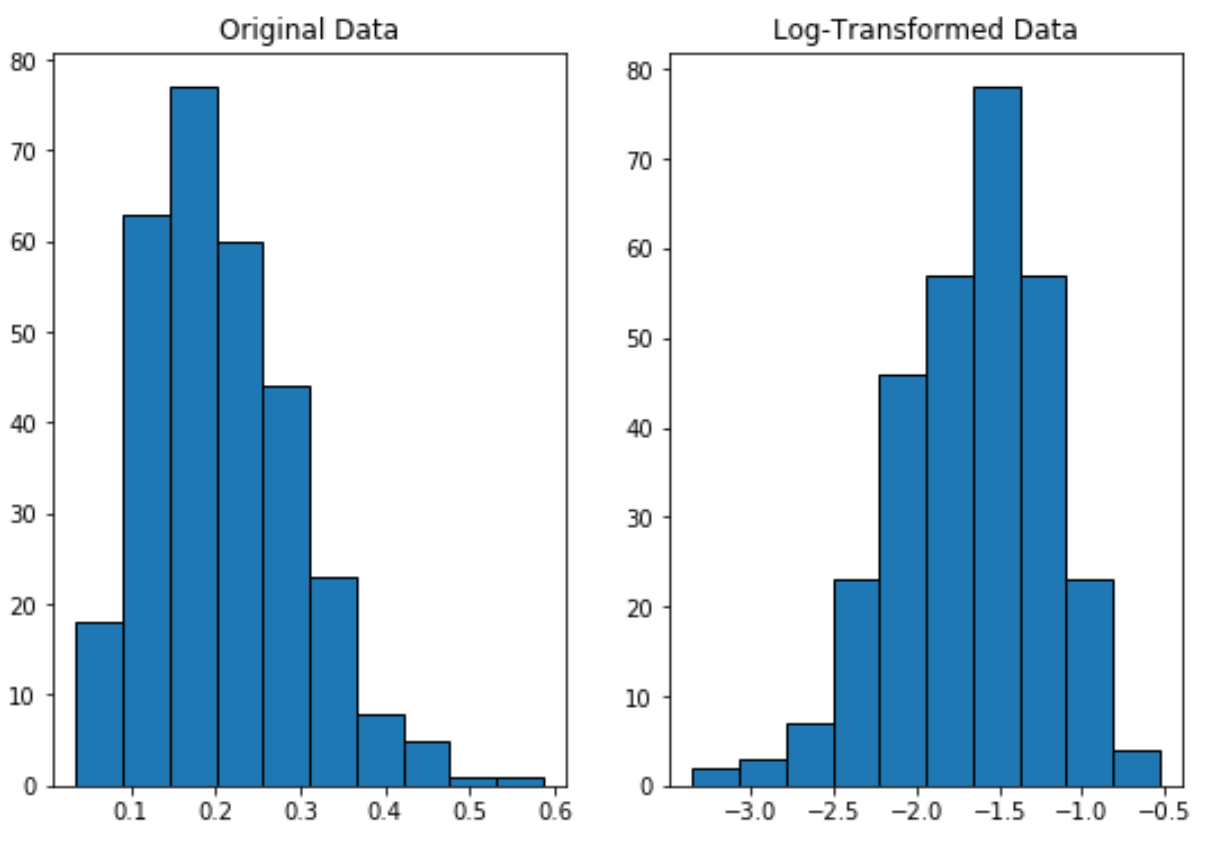
Observe como a distribuição transformada em logaritmo é distribuída mais normalmente do que a distribuição original.
Ainda não tem um “formato de sino” perfeito, mas está mais próximo de uma distribuição normal do que da distribuição original.
Transformação de raiz quadrada em Python
O código a seguir mostra como realizar uma transformação de raiz quadrada em uma variável e criar gráficos lado a lado para exibir a distribuição original e a distribuição transformada de raiz quadrada dos dados:
import numpy as np import matplotlib. pyplot as plt #make this example reproducible n.p. random . seeds (0) #create beta distributed random variable with 200 values data = np. random . beta (a= 1 , b= 5 , size= 300 ) #create log-transformed data data_log = np. sqrt (data) #define grid of plots fig, axs = plt. subplots (nrows= 1 , ncols= 2 ) #create histograms axs[0]. hist (data, edgecolor=' black ') axs[1]. hist (data_log, edgecolor=' black ') #add title to each histogram axs[0]. set_title (' Original Data ') axs[1].set_title(' Square Root Transformed Data ')
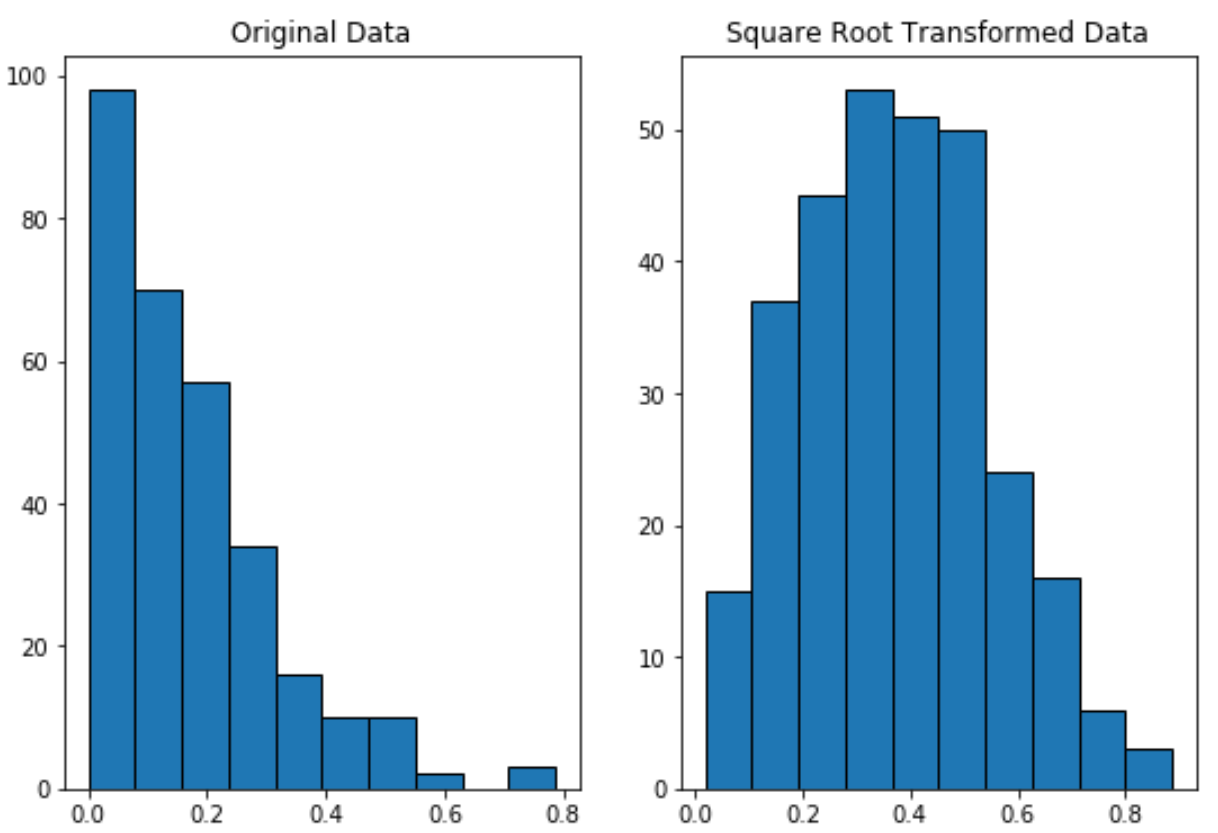
Observe como os dados transformados pela raiz quadrada são distribuídos muito mais normalmente do que os dados originais.
Transformação de raiz cúbica em Python
O código a seguir mostra como executar uma transformação de raiz cúbica em uma variável e criar gráficos lado a lado para exibir a distribuição original e a distribuição transformada de raiz cúbica dos dados:
import numpy as np import matplotlib. pyplot as plt #make this example reproducible n.p. random . seeds (0) #create beta distributed random variable with 200 values data = np. random . beta (a= 1 , b= 5 , size= 300 ) #create log-transformed data data_log = np. cbrt (data) #define grid of plots fig, axs = plt. subplots (nrows= 1 , ncols= 2 ) #create histograms axs[0]. hist (data, edgecolor=' black ') axs[1]. hist (data_log, edgecolor=' black ') #add title to each histogram axs[0]. set_title (' Original Data ') axs[1].set_title(' Cube Root Transformed Data ')
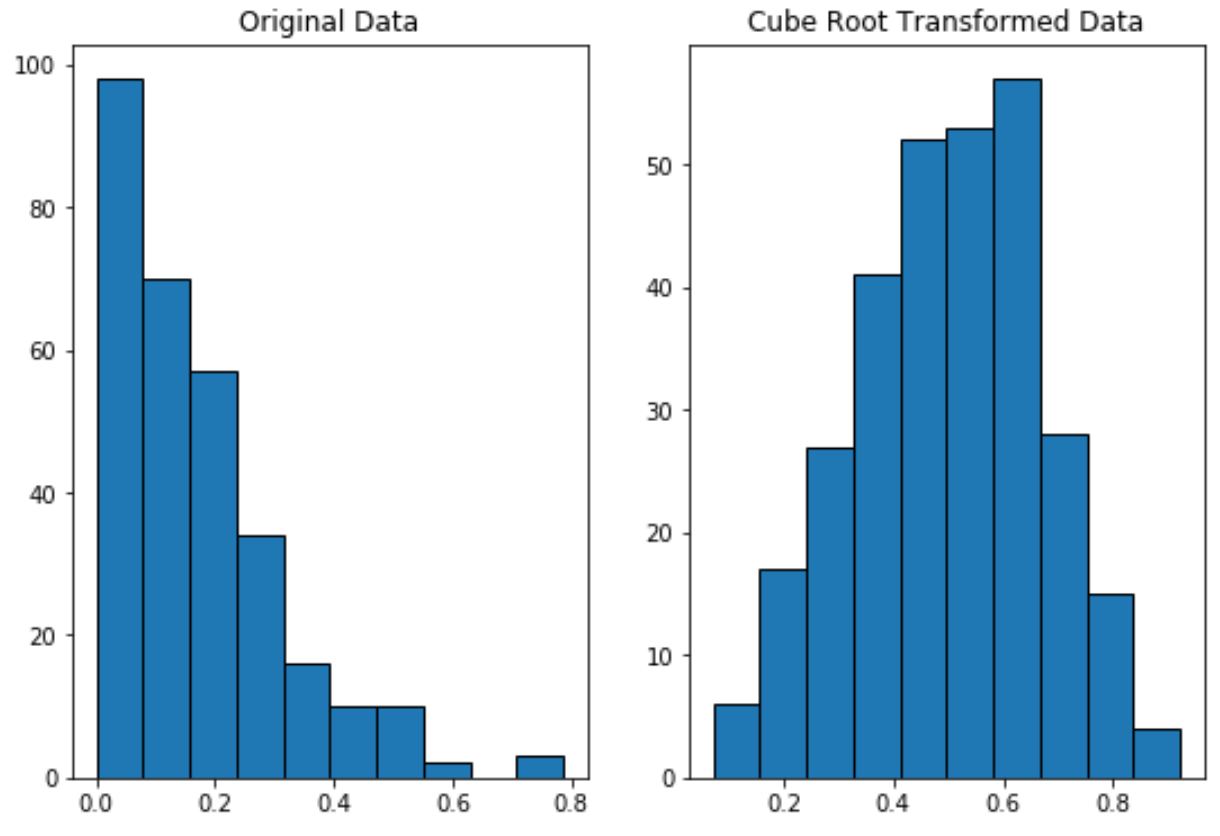
Observe como os dados transformados da raiz cúbica são distribuídos muito mais normalmente do que os dados originais.
Recursos adicionais
Como calcular pontuações Z em Python
Como normalizar dados em Python
Qual é a suposição de normalidade nas estatísticas?