Como testar a normalidade em r (4 métodos)

Muitos testes estatísticos assumem que os conjuntos de dados são normalmente distribuídos.

Existem quatro maneiras comuns de verificar essa suposição em R:

1. (Método visual) Crie um histograma.

• Se o histograma tiver aproximadamente o formato de um “sino”, então os dados serão considerados normalmente distribuídos.

2. (Método visual) Crie um gráfico QQ.

• Se os pontos no gráfico estiverem aproximadamente ao longo de uma linha reta diagonal, então os dados são considerados normalmente distribuídos.

3. (Teste estatístico formal) Realize um teste de Shapiro-Wilk.

• Se o valor p do teste for maior que α = 0,05, então os dados são considerados normalmente distribuídos.

4. (Teste estatístico formal) Realize um teste de Kolmogorov-Smirnov.

• Se o valor p do teste for maior que α = 0,05, então os dados são considerados normalmente distribuídos.

Os exemplos a seguir mostram como usar cada um desses métodos na prática.

Método 1: crie um histograma

O código a seguir mostra como criar um histograma para um conjunto de dados normalmente distribuído e não normalmente distribuído em R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create histogram for both datasets
hist(normal_data, col=' steelblue ', main=' Normal ')
hist(non_normal_data, col=' steelblue ', main=' Non-normal ') 

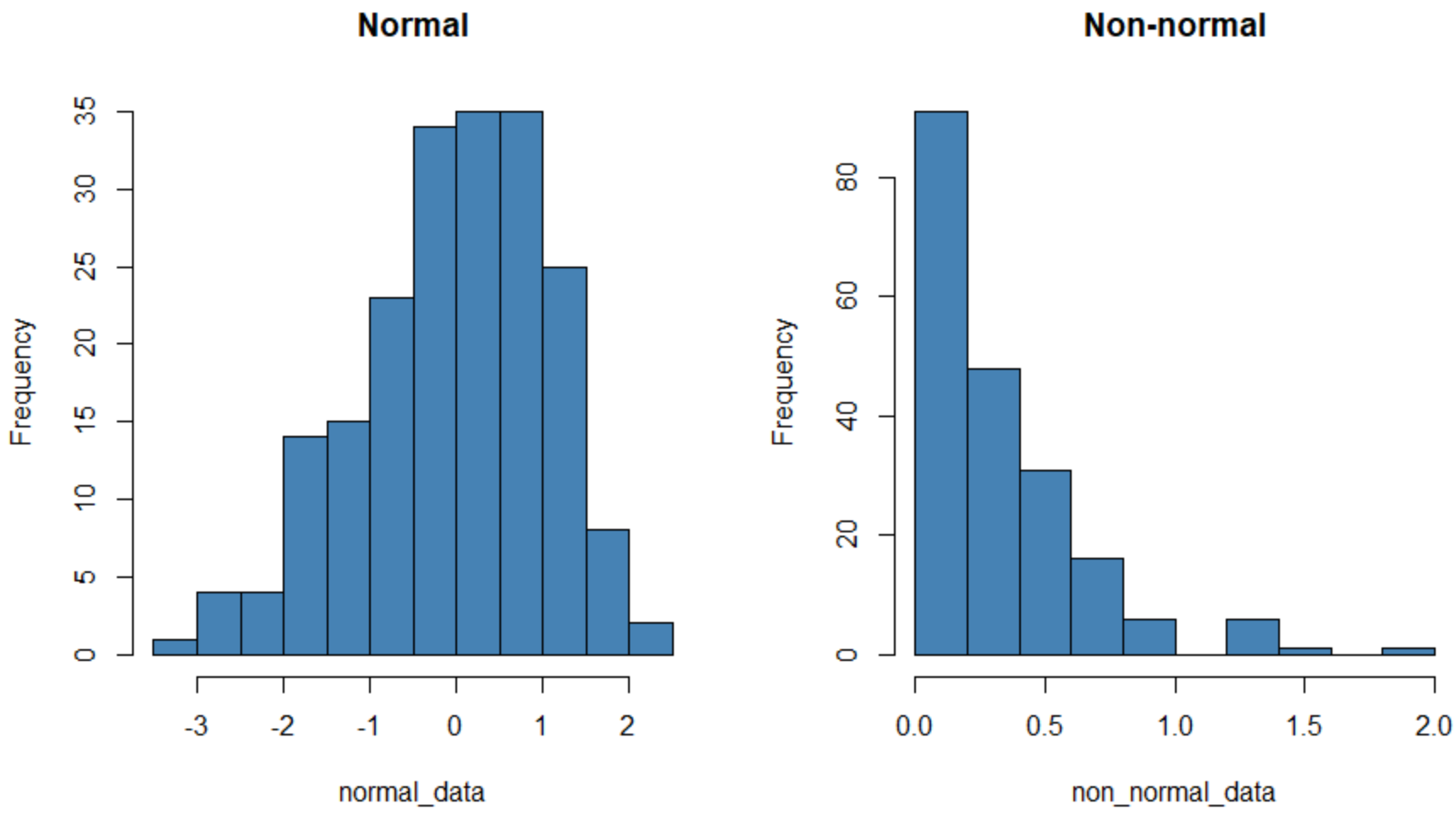
O histograma à esquerda mostra um conjunto de dados que é normalmente distribuído (aproximadamente em forma de “sino”) e o da direita mostra um conjunto de dados que não é normalmente distribuído.

Método 2: criar um gráfico QQ

O código a seguir mostra como criar um gráfico QQ para um conjunto de dados normalmente distribuído e não normalmente distribuído em R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create QQ plot for both datasets
qqnorm(normal_data, main=' Normal ')
qqline(normal_data)

qqnorm(non_normal_data, main=' Non-normal ')
qqline(non_normal_data)

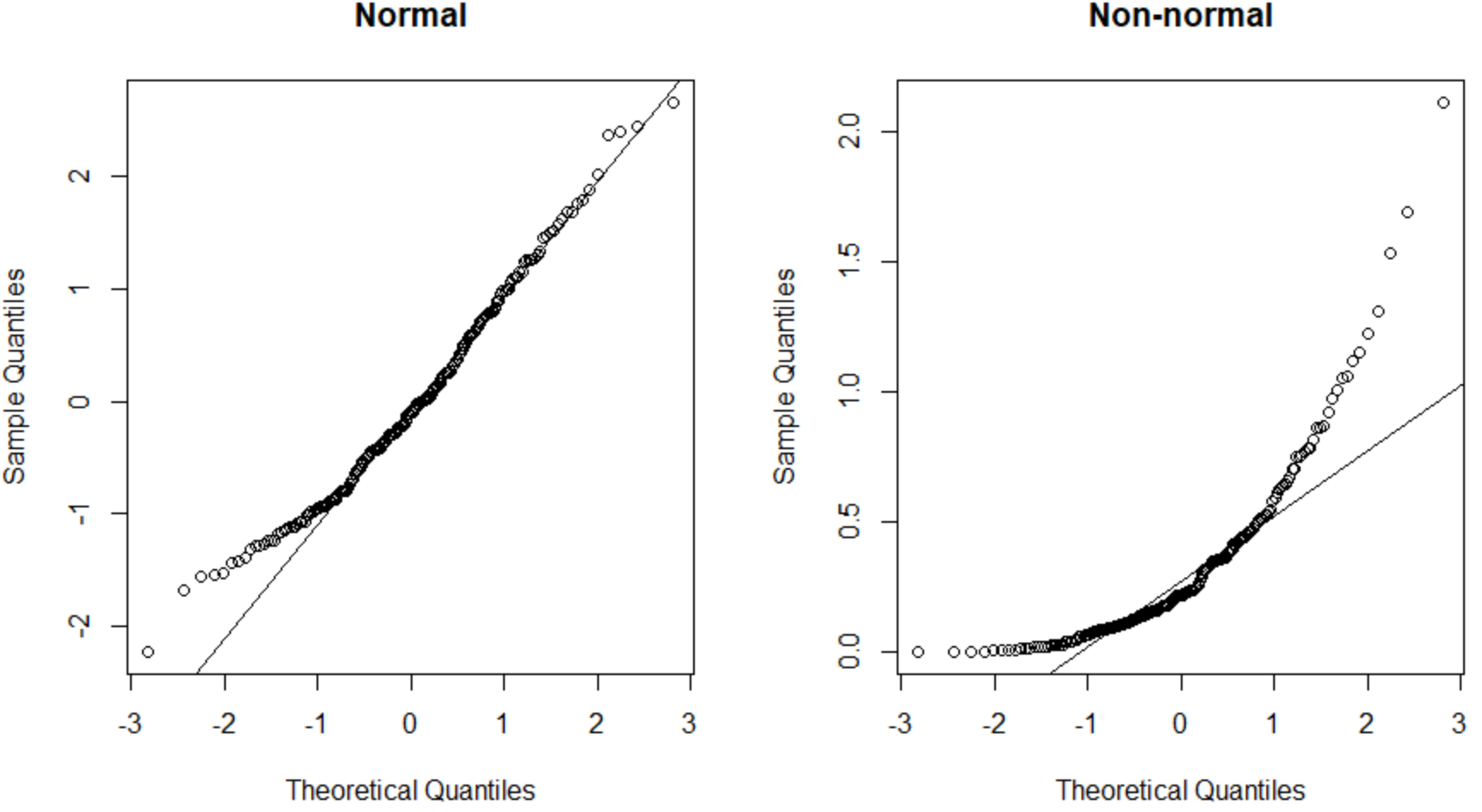
O gráfico QQ à esquerda apresenta um conjunto de dados normalmente distribuído (os pontos caem ao longo de uma linha reta diagonal) e o gráfico QQ à direita apresenta um conjunto de dados que não é normalmente distribuído.

Método 3: realizar um teste de Shapiro-Wilk

O código a seguir mostra como realizar um teste de Shapiro-Wilk em um conjunto de dados normalmente distribuído e não normalmente distribuído em R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform shapiro-wilk test
shapiro. test (normal_data)

	Shapiro-Wilk normality test

data: normal_data
W = 0.99248, p-value = 0.3952

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform shapiro-wilk test
shapiro. test (non_normal_data)

	Shapiro-Wilk normality test

data: non_normal_data
W = 0.84153, p-value = 1.698e-13

O valor p do primeiro teste não é inferior a 0,05, o que indica que os dados estão normalmente distribuídos.

O valor p do segundo teste é inferior a 0,05, indicando que os dados não têm distribuição normal.

Método 4: realizar um teste de Kolmogorov-Smirnov

O código a seguir mostra como realizar um teste de Kolmogorov-Smirnov em um conjunto de dados normalmente distribuído e não normalmente distribuído em R:

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform kolmogorov-smirnov test
ks. test (normal_data, ' pnorm ')

	One-sample Kolmogorov–Smirnov test

data: normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform kolmogorov-smirnov test
ks. test (non_normal_data, ' pnorm ') 
	One-sample Kolmogorov–Smirnov test

data: non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided

O valor p do primeiro teste não é inferior a 0,05, o que indica que os dados estão normalmente distribuídos.

O valor p do segundo teste é inferior a 0,05, indicando que os dados não têm distribuição normal.

Como lidar com dados não normais

Se um determinado conjunto de dados não for normalmente distribuído, muitas vezes podemos realizar uma das seguintes transformações para torná-lo mais normalmente distribuído:

1. Transformação de log: transforme valores de x em log(x) .

2. Transformação de raiz quadrada: Transforme os valores de x em √x .

3. Transformação da raiz cúbica: transforme os valores de x em x ^1/3 .

Ao realizar essas transformações, o conjunto de dados geralmente se torna distribuído de forma mais normal.

Leia este tutorial para ver como realizar essas transformações em R.

Recursos adicionais

Como criar histogramas em R
Como criar e interpretar um gráfico QQ em R
Como realizar um teste de Shapiro-Wilk em R
Como realizar um teste de Kolmogorov-Smirnov em R