Mae vs. rmse: qual métrica você deve usar?

Modelos de regressão são usados para quantificar a relação entre uma ou mais variáveis preditoras e uma variável de resposta .

Sempre que ajustamos um modelo de regressão, queremos entender quão bem o modelo é capaz de usar os valores das variáveis preditoras para prever o valor da variável resposta.

Duas métricas que costumamos usar para quantificar quão bem um modelo se ajusta a um conjunto de dados são o erro médio absoluto (MAE) e a raiz do erro quadrático médio (RMSE), que são calculados da seguinte forma:

MAE : Uma métrica que nos informa a diferença média absoluta entre os valores previstos e os valores reais em um conjunto de dados. Quanto menor o MAE, melhor o modelo se ajusta a um conjunto de dados.

MAE = 1/n * Σ|y _i – ŷ _i |

Ouro:

• Σ é um símbolo que significa “soma”
• y _i é o valor observado para a ^i-ésima observação
• ŷ _i é o valor previsto para a i- ^ésima observação
• n é o tamanho da amostra

RMSE : Uma métrica que nos informa a raiz quadrada da diferença quadrática média entre os valores previstos e os valores reais em um conjunto de dados. Quanto menor o RMSE, melhor o modelo se ajusta a um conjunto de dados.

É calculado da seguinte forma:

RMSE = √ Σ(y _i – ŷ _i ) ² / n

Ouro:

• Σ é um símbolo que significa “soma”
• ŷ _i é o valor previsto para a i- ^ésima observação
• y _i é o valor observado para a ^i-ésima observação
• n é o tamanho da amostra

Exemplo: Cálculo de RMSE e MAE

Suponha que usemos um modelo de regressão para prever quantos pontos 10 jogadores marcarão em um jogo de basquete.

A tabela a seguir mostra os pontos previstos pelo modelo em comparação com os pontos reais marcados pelos jogadores:

Usando a calculadora MAE, podemos calcular que o MAE é 3,2.

Isso nos diz que a diferença absoluta média entre os valores previstos pelo modelo e os valores reais é de 3,2.

Usando a calculadora RMSE , podemos calcular que o RMSE é igual a 4 .

Isso nos diz que a raiz quadrada da raiz quadrada média das diferenças entre os pontos marcados previstos e os pontos marcados reais é 4.

Observe que cada métrica nos dá uma ideia da diferença típica entre o valor previsto feito pelo modelo e o valor real no conjunto de dados, mas a interpretação de cada métrica é um pouco diferente.

RMSE vs. MAE: qual métrica você deve usar?

Se você quiser atribuir mais peso às observações que estão mais distantes da média (ou seja, se um desvio de 20 for duas vezes pior que um desvio de 10), é melhor usar o RMSE para medir o erro, porque o RMSE é mais sensível a observações mais distantes da média.

No entanto, se estar “compensado” em 20 é duas vezes pior do que estar “compensado” em 10, então é melhor usar o MAE.

Para ilustrar isso, suponha que temos um jogador que é claramente atípico em termos de número de pontos marcados:

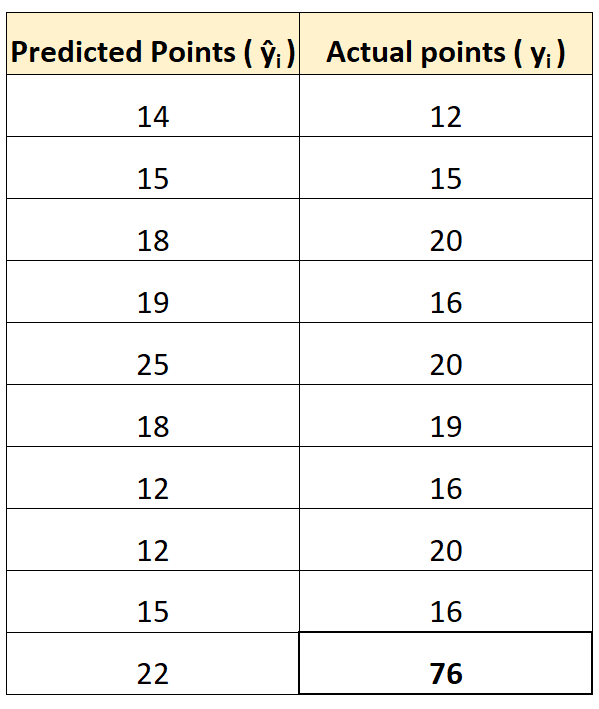
Usando as calculadoras online mencionadas anteriormente, podemos calcular o MAE e o RMSE como:

• MAE : 8
• REQM : 16.4356

Observe que o RMSE aumenta muito mais que o MAE.

Isso ocorre porque o RMSE usa diferenças quadradas em sua fórmula e a diferença quadrada entre o valor observado de 76 e o valor previsto de 22 é bastante grande. Isso resulta em um aumento significativo no valor RMSE.

Na prática, normalmente ajustamos vários modelos de regressão a um conjunto de dados e calculamos apenas uma dessas métricas para cada modelo.

Por exemplo, poderíamos ajustar três modelos de regressão diferentes e calcular o RMSE para cada modelo. Selecionaríamos então o modelo com o menor valor de RMSE como o “melhor” modelo, porque é aquele que faz as previsões mais próximas dos valores reais no conjunto de dados.

Em ambos os casos, certifique-se de calcular a mesma métrica para cada modelo. Por exemplo, não calcule o MAE para um modelo e o RMSE para outro modelo e depois compare estas duas medições.

Recursos adicionais

Os tutoriais a seguir explicam como calcular o MAE usando diferentes softwares estatísticos:

Como calcular o erro médio absoluto no Excel
Como calcular o erro médio absoluto em R
Como calcular o erro médio absoluto em Python

Os tutoriais a seguir explicam como calcular o RMSE usando diferentes softwares estatísticos:

Como calcular o erro quadrático médio no Excel
Como calcular o erro quadrático médio em R
Como calcular o erro quadrático médio em Python