Distribuição lognormal
Este artigo explica o que é distribuição lognormal nas estatísticas. Assim, você descobrirá quais são as propriedades da distribuição lognormal e o gráfico desse tipo de distribuição de probabilidade.
Qual é a distribuição lognormal?
A distribuição lognormal , ou distribuição lognormal , é uma distribuição de probabilidade que define uma variável aleatória cujo logaritmo segue uma distribuição normal.
Portanto, se a variável X tem distribuição normal, então a função exponencial e x tem distribuição lognormal.
![]()
Observe que a distribuição lognormal só pode ser usada quando os valores das variáveis são positivos, pois o logaritmo é uma função que leva apenas um argumento positivo.
Entre as diferentes aplicações da distribuição lognormal em estatística, destacamos a utilização desta distribuição para analisar investimentos financeiros e realizar análises de confiabilidade.
A distribuição lognormal também é conhecida como distribuição Tinaut , às vezes também escrita como distribuição lognormal ou distribuição log-normal .
Gráfico de distribuição lognormal
Agora que conhecemos a definição da distribuição lognormal, veremos nesta seção como a representação gráfica da distribuição lognormal varia dependendo dos valores de sua média aritmética e de seu desvio padrão.
O gráfico da função densidade da distribuição lognormal é o seguinte:
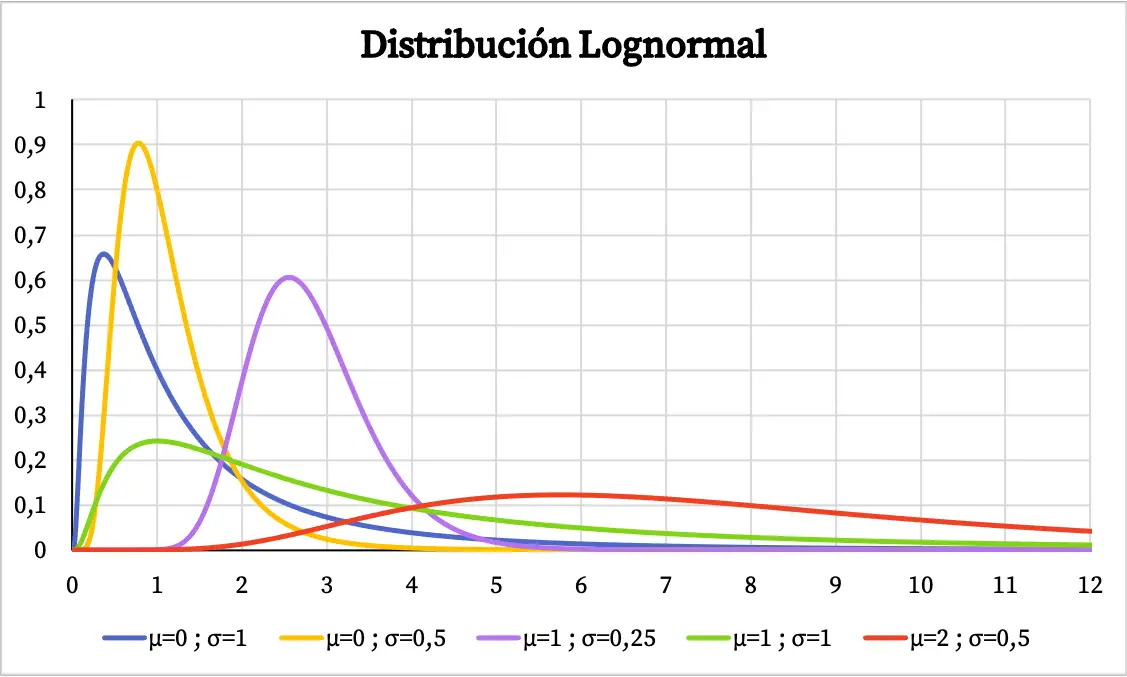
Por outro lado, o gráfico de probabilidade cumulativa da distribuição lognormal é o seguinte:
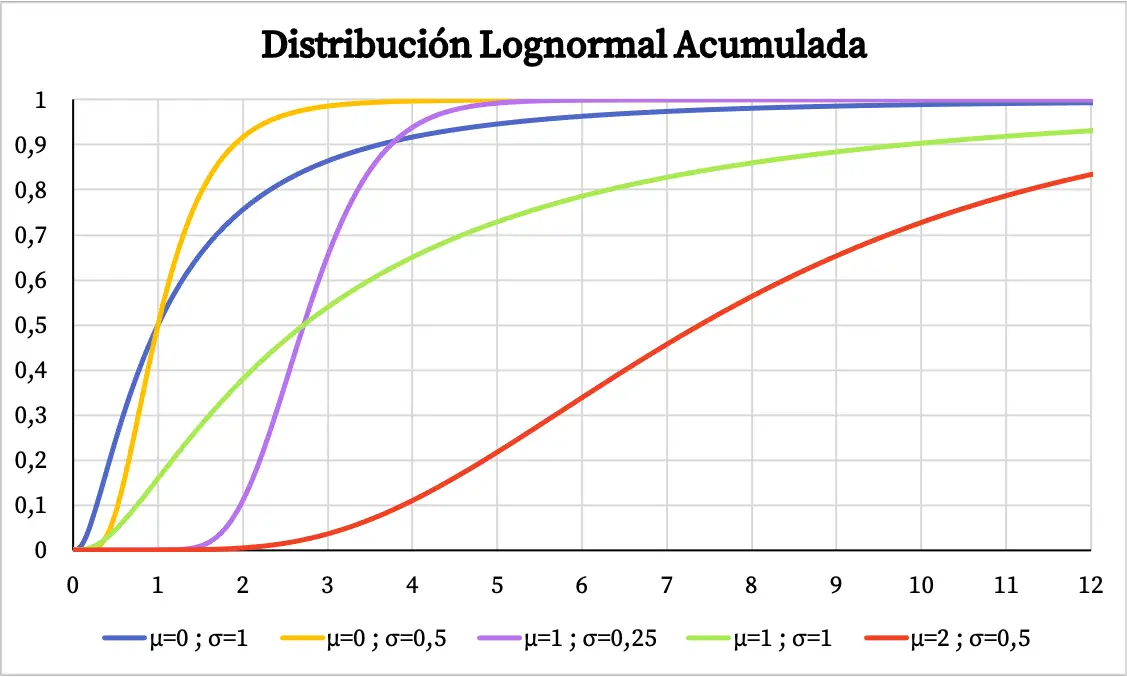
Características da distribuição lognormal
A distribuição lognormal possui as seguintes características:
- A distribuição lognormal é definida pelo valor de dois parâmetros, sua média aritmética μ e sua variância σ 2 .
![]()
- O domínio da distribuição lognormal consiste em números reais positivos, pois o logaritmo não aceita valores negativos ou zero.
![]()
- A expectativa de uma distribuição lognormal é igual ao número e elevado à soma da média mais a variância dividida por dois.
![]()
- Por outro lado, a variância de uma distribuição lognormal pode ser calculada com a seguinte expressão:
![]()
- A moda da distribuição lognormal é equivalente ao número e elevado à média da distribuição.
![]()
- O coeficiente de assimetria da distribuição lognormal pode ser determinado aplicando a seguinte fórmula:
![]()
- A fórmula para a função densidade da distribuição lognormal é:
![]()
- A fórmula para a função de probabilidade cumulativa da distribuição lognormal é:
![]()
Ouro
![]()
é a função de probabilidade cumulativa de uma distribuição normal padrão .
- A média aritmética de uma distribuição lognormal é maior que o valor de sua mediana.
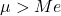
About Author
Dr. benjamim anderson
Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais