Distribuição binomial negativa
Este artigo explica o que é a distribuição binomial negativa e para que ela é usada. Você também encontrará a fórmula da distribuição binomial negativa, um exemplo concreto e as propriedades deste tipo de distribuição de probabilidade. Finalmente, você poderá calcular qualquer probabilidade de distribuição binomial negativa com uma calculadora online.
Qual é a distribuição binomial negativa?
A distribuição binomial negativa é uma distribuição de probabilidade que descreve o número de tentativas de Bernoulli necessárias para obter um determinado número de resultados positivos.
Portanto, uma distribuição binomial negativa tem dois parâmetros característicos: r é o número de resultados desejados e p é a probabilidade de sucesso para cada experimento de Bernoulli realizado.
![]()
Lembre-se de que um teste de Bernoulli é um experimento que tem dois resultados possíveis: “sucesso” e “fracasso”. Portanto, se a probabilidade de “sucesso” for p , a probabilidade de “fracasso” é q=1-p .
Assim, uma distribuição binomial negativa define um processo no qual são realizadas quantas tentativas de Bernoulli forem necessárias para obter resultados positivos. Além disso, todos estes ensaios de Bernoulli são independentes e têm uma probabilidade constante de sucesso .
Por exemplo, uma variável aleatória que segue uma distribuição binomial negativa é o número de vezes que um dado deve ser lançado até que o número 6 seja lançado três vezes.
A diferença entre uma distribuição binomial negativa e uma distribuição binomial é que a distribuição binomial negativa conta o número de vezes que leva para obter um certo número de resultados bem-sucedidos, enquanto a distribuição binomial conta o número de casos bem-sucedidos em uma série de testes de Bernoulli.
Fórmula de distribuição binomial negativa
Dados os parâmetros r, p, x, a probabilidade de uma distribuição binomial negativa é calculada multiplicando o número combinatório de x-1 em xr por (1-p) xr por p r .
Portanto, a fórmula para calcular uma probabilidade de distribuição binomial negativa é:

👉 Você pode usar a calculadora abaixo para calcular a probabilidade de uma variável que segue a distribuição binomial negativa.
Exercício resolvido da distribuição binomial negativa
- Qual é a probabilidade de que, se você lançar uma moeda oito vezes, ela dê cara pela quarta vez no oitavo lançamento?
Primeiro, precisamos calcular a probabilidade de obter cara no lançamento de uma moeda. Neste caso, temos apenas um resultado positivo (cara) entre dois resultados possíveis (cara e coroa), então a probabilidade de sucesso é:
![]()
Assim, a variável aleatória neste problema segue uma distribuição binomial negativa onde r=4 ep=0,5. Portanto, usamos a fórmula da distribuição binomial negativa para calcular a probabilidade que o exercício nos pede para fazer.
![Rendered by QuickLaTeX.com \begin{aligned}P[X=x]&=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r\\[2ex]\displaystyle P[X=8]&=\begin{pmatrix}8-1\\ 8-4\end{pmatrix}\cdot (1-0,5)^{8-4}\cdot 0,5^4\\[2ex] P[X=8]&=0,1367\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-bc56100604e5889a6d169c0395f19ebe_l3.png)
Características da distribuição binomial negativa
Abaixo estão as características mais importantes da distribuição binomial negativa.
- A distribuição binomial negativa é definida por dois parâmetros característicos: r é o número de resultados desejados com sucesso e p é a probabilidade de sucesso para cada experimento de Bernoulli realizado.
*** QuickLaTeX cannot compile formula:
\begin{array}{c}r\in \mathbb{Z}^+ \\[2ex] 0 <ul><li> The mean of the negative binomial distribution is equal to <em>r</em> multiplied by <em>(1-p)</em> and divided by <em>p</em> . Thus the formula which makes it possible to calculate the mean of a negative binomial distribution is the following: </li></ul>[latex]E[X]=\cfrac{r\cdot (1-p)}{p}
*** Error message:
Missing $ inserted.
leading text: \begin{array}{c}
Please use \mathaccent for accents in math mode.
leading text: ...The mean of the binomial distribution born
Please use \mathaccent for accents in math mode.
leading text: ... the negative binomial distribution is
Please use \mathaccent for accents in math mode.
leading text: ...negative binomial distribution is equal to
Please use \mathaccent for accents in math mode.
leading text: ...gative is equal to <em>r</em> multiplied
Please use \mathaccent for accents in math mode.
leading text: ...m> multiplied by <em>(1-p)</em> and divided
Please use \mathaccent for accents in math mode.
leading text: ...the mean of a binomial distribution born
\begin{array} on input line 8 ended by \end{document}.
- A variância de uma distribuição binomial negativa é igual a r multiplicado por (1-p) dividido por p 2 .
![]()
- Se o parâmetro r for maior que 1, a moda de uma distribuição binomial negativa pode ser calculada com a seguinte fórmula:
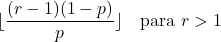
![]()
- O coeficiente de assimetria de uma distribuição binomial negativa é calculado com a seguinte expressão:
![]()
- A curtose de uma distribuição binomial negativa pode ser encontrada com a seguinte fórmula:
![]()
- Se o parâmetro r for igual a 1, então temos um caso de distribuição geométrica .
![]()
Calculadora de distribuição binomial negativa
Insira os valores dos parâmetros r, p, x na calculadora a seguir para calcular a probabilidade. Você deve inserir números usando o ponto como separador decimal, por exemplo 0,50.