Distribuição exponencial

By Dr. benjamim anderson Agosto 3, 2023 Probabilidade 0 Comments

Este artigo explica o que é a distribuição exponencial nas estatísticas e para que ela é usada. Da mesma forma, você encontrará quais são as propriedades da distribuição exponencial bem como suas fórmulas, seu gráfico e um exercício resolvido. Além disso, você poderá calcular qualquer probabilidade com uma calculadora online de distribuição exponencial.

O que é distribuição exponencial?

A distribuição exponencial é uma distribuição de probabilidade contínua usada para modelar o tempo de espera para a ocorrência de um fenômeno aleatório.

Mais precisamente, a distribuição exponencial permite descrever o tempo de espera entre dois eventos que segue uma distribuição de Poisson. Portanto, a distribuição exponencial está intimamente relacionada com a distribuição de Poisson.

➤ Veja: Qual é a distribuição de Poisson?

A distribuição exponencial possui um parâmetro característico, representado pela letra grega λ e indica o número de vezes que se espera que o evento estudado ocorra durante um determinado período de tempo.

$X\sim \text{Exp}(\lambda)$

Da mesma forma, a distribuição exponencial também é usada para modelar o tempo até que ocorra uma falha. A distribuição exponencial, portanto, tem diversas aplicações na teoria da confiabilidade e da sobrevivência.

Exemplos de distribuições exponenciais

Agora que conhecemos a definição de distribuição exponencial, vejamos vários exemplos desse tipo de distribuição para entender melhor o conceito.

Exemplos de distribuição exponencial:

O tempo decorrido entre duas chamadas em uma central de atendimento.
O tempo que uma pessoa tem que esperar até que um táxi gratuito passe em uma rua específica.
O tempo de espera até que um novo cliente entre em uma loja.
O tempo decorrido entre dois usuários diferentes entrando em uma página da web.
Tempo decorrido num aeroporto entre a decolagem de um avião e a saída de outro.

Fórmula de distribuição exponencial

A fórmula da função densidade que define o cálculo de uma distribuição de probabilidade exponencial é igual a λ multiplicado pelo número e elevado à potência de λ negativo vezes x.

Em outras palavras, a fórmula para calcular uma probabilidade de distribuição exponencial é a seguinte:

👉 Você pode usar a calculadora abaixo para calcular a probabilidade de uma variável que segue a distribuição exponencial.

Por outro lado, a fórmula para calcular uma probabilidade cumulativa da distribuição exponencial é a seguinte:

$P[X\leq x]=1-e^{-\lambda x}$

Gráfico de distribuição exponencial

Nesta seção você pode ver a representação gráfica da função densidade e da função distribuição da distribuição exponencial.

Abaixo você pode ver como o gráfico da função densidade da distribuição exponencial varia em função do valor do parâmetro λ.

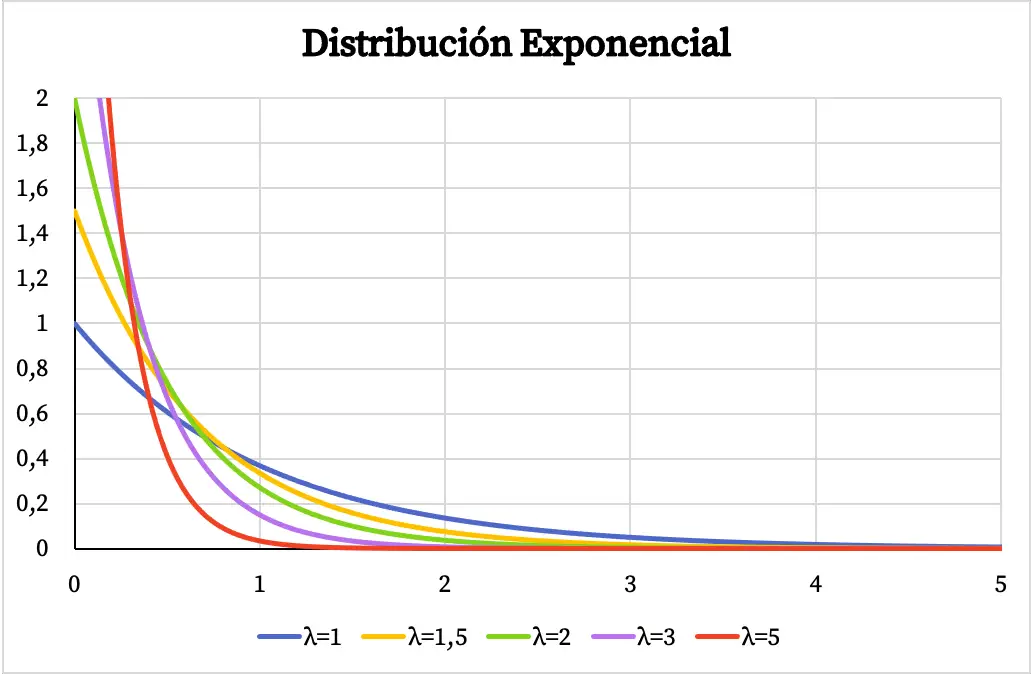
Da mesma forma, a função de probabilidade cumulativa da distribuição exponencial também depende do valor do parâmetro λ, como você pode ver no gráfico a seguir:

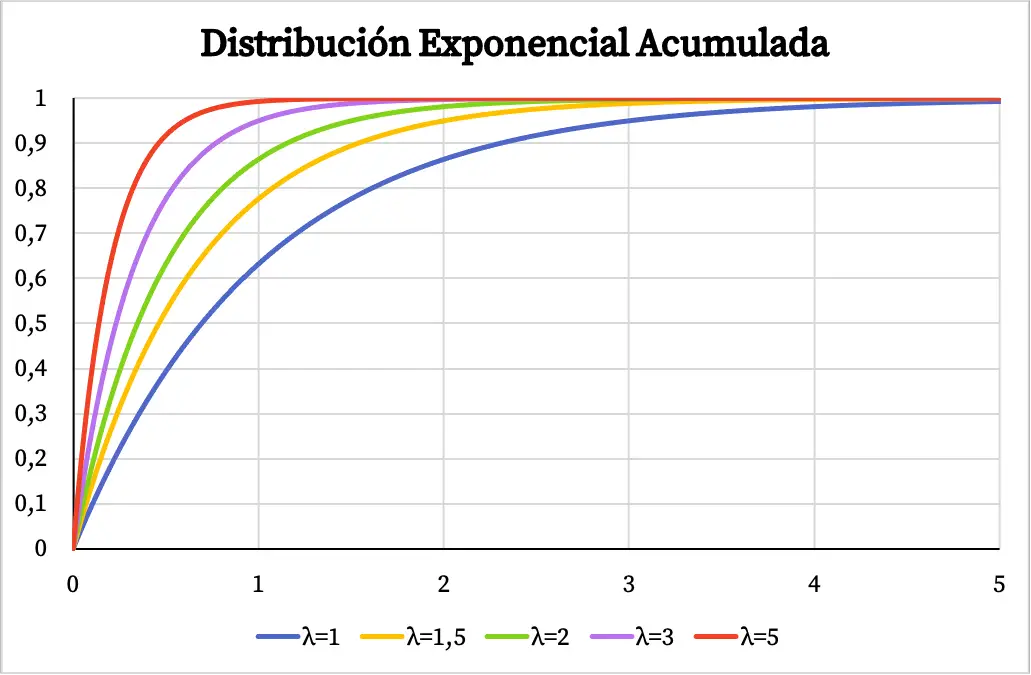
gráfico de probabilidade de distribuição cumulativa exponencial

Exercício resolvido sobre distribuição exponencial

Em média, λ=1 usuários/min acessam uma página da web específica. Qual é a probabilidade de que o tempo entre a entrada de dois usuários seja de 3 minutos? E a probabilidade de ser igual ou inferior a 2 minutos?

A distribuição que define a variável aleatória deste problema é uma distribuição exponencial, pois estudamos o tempo que passa desde o momento em que ocorre um evento (a entrada de um usuário na página web) até que esse mesmo evento aconteça novamente.

$X\sim \text{Exp}(1)$

Portanto, para calcular a probabilidade de o tempo decorrido entre a entrada de dois usuários diferentes ser de três minutos, precisamos aplicar a fórmula da função densidade (ver acima):

$\begin{aligned}P[X=x]&=\lambda e^{-\lambda x}\\[2ex]P[X=3]&=1\cdot e^{-1\cdot 3}\\[2ex]P[X=3]&=0,05\end{aligned}$

Por outro lado, para determinar uma probabilidade cumulativa, devemos usar a fórmula da função de distribuição da distribuição exponencial:

$\begin{aligned}P[X\leq x]&=1- e^{-\lambda x}\\[2ex]P[X\leq 2]&=1-e^{-1\cdot 2}\\[2ex]P[X\leq 2]&=0,86\end{aligned}$

Características da distribuição exponencial

A distribuição exponencial tem as seguintes características:

A distribuição exponencial possui um parâmetro característico, λ, que indica o número de vezes que se espera que o fenômeno estudado ocorra durante um determinado período de tempo.

$X\sim \text{Exp}(\lambda)$

A distribuição exponencial não pode assumir um valor negativo, portanto o domínio da distribuição exponencial consiste em todos os números reais maiores ou iguais a zero.

$x\in [0,+\infty)$

A média da distribuição exponencial é igual a um dividido pelo parâmetro característico λ.

$E[X]=\cfrac{1}{\lambda}$

A variância da distribuição exponencial é o quadrado de sua média, portanto a variância da distribuição exponencial é equivalente a um sobre o coeficiente λ ao quadrado.

$Var(X)=\cfrac{1}{\lambda^2 }$

Qualquer que seja o valor de λ, o coeficiente de assimetria da distribuição exponencial é sempre igual a 2.

$A=2$

Da mesma forma, o coeficiente de curtose de qualquer distribuição exponencial é sempre equivalente a 9.

$C=9$

A fórmula para a função densidade da distribuição exponencial é:

$P[X=x]=\lambda e^{-\lambda x}$

Embora a fórmula para a função de probabilidade cumulativa da distribuição exponencial seja a seguinte:

$P[X\leq x]=1-e^{-\lambda x}$

A distribuição exponencial é uma das poucas distribuições de probabilidade com a propriedade de falta de memória. Esta propriedade significa que a ocorrência de um evento anterior não afeta a probabilidade desse evento ocorrer no futuro. Por exemplo, em uma distribuição exponencial, a probabilidade de um novo usuário acessar uma página da Web em menos de um minuto não depende de o usuário ter acabado de entrar ou de nenhum usuário ter entrado desde então. mais de dez minutos.

$P[X>x+y|X>y]=P[X>x]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”254″ style=”vertical-align: -5px;”></p> </p> <h2 class=$ Calculadora de distribuição exponencial

Insira o valor do parâmetro λ e o valor de x na calculadora a seguir para calcular a probabilidade. Você precisa selecionar a probabilidade que deseja calcular e inserir os números usando o ponto como separador decimal, por exemplo 0,50.

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais