A causalidade implica correlação? (3 exemplos)
É bem sabido que correlação não implica causalidade .
Como um exemplo simples, se coletássemos dados todos os anos sobre o número total de graduados do ensino médio e o consumo total de pizza nos Estados Unidos, descobriríamos que as duas variáveis estão altamente correlacionadas:
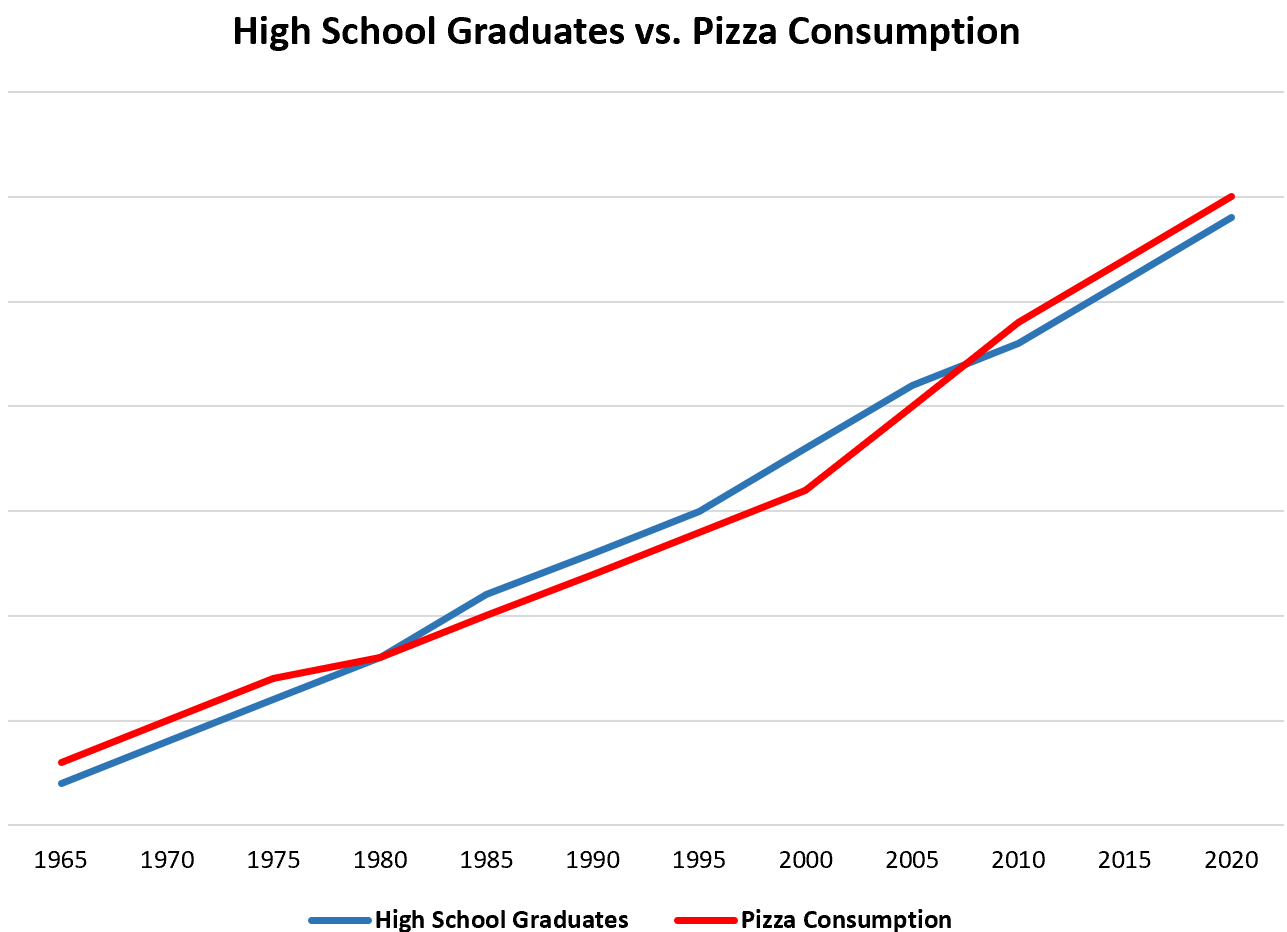
Isso não significa que o aumento do número de concluintes do ensino médio leve ao aumento do consumo de pizza.
A explicação mais provável é que a população dos EUA aumentou ao longo do tempo, o que significa que o número de pessoas com diploma do ensino secundário e a quantidade total de pizza consumida aumentam à medida que a população aumenta.
Mas e quanto à afirmação oposta: a causalidade implica correlação?
Se uma variável causa outra variável, isso significa necessariamente que as duas variáveis estarão correlacionadas?
A resposta curta: Não.
Os exemplos a seguir mostram o porquê.
Exemplo 1: relação quadrática
Suponha que uma variável, X, faça com que a variável Y assuma um valor igual a X 2 .
Por exemplo:
- Se X = -10 então Y = -10 2 = 100
- Se X = 0 então Y = 0 2 = 0
- Se X = 10 então Y = 10 2 = 100
E assim por diante.
Se traçarmos a relação entre X e Y, ficaria assim:
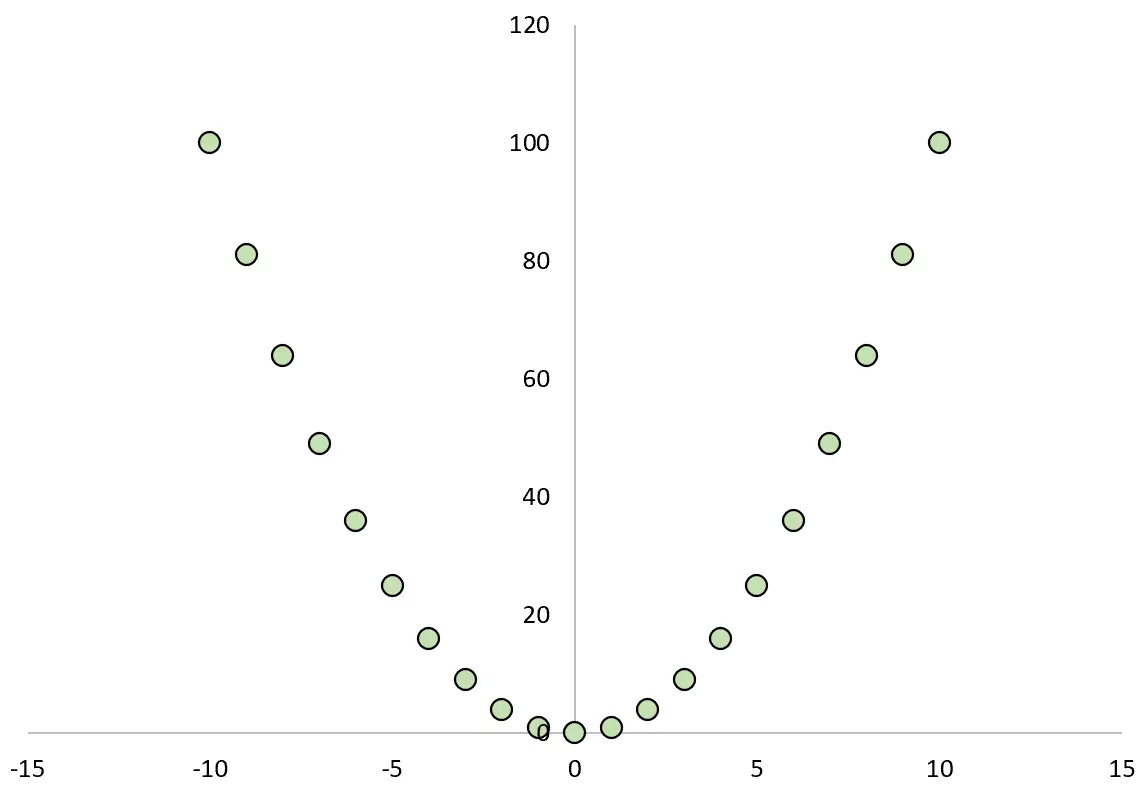
Se calculássemos o coeficiente de correlação de Pearson entre as duas variáveis, descobriríamos que a correlação é zero .
Embora X cause Y, a correlação linear entre as duas variáveis é zero.
Exemplo 2: relação quártica
Suponha que uma variável, X, faça com que a variável Y assuma um valor igual a X 4 .
Por exemplo:
- Se X = -10 então Y = -10 4 = 10.000
- Se X = 0 então Y = 0 4 = 0
- Se X = 10 então Y = 10 4 = 10.000
E assim por diante.
Se traçarmos a relação entre X e Y, ficaria assim:
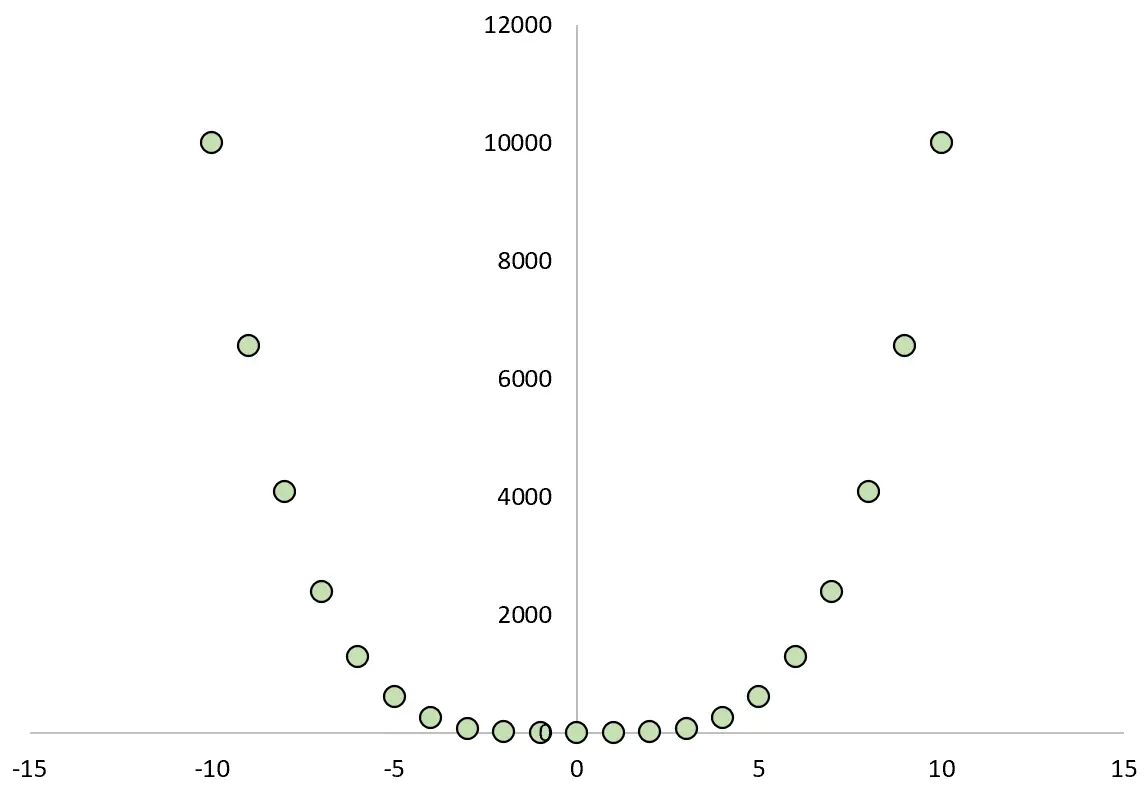
Se calculássemos o coeficiente de correlação de Pearson entre as duas variáveis, descobriríamos que a correlação é zero .
Sabemos que X causa Y, mas a correlação linear entre as duas variáveis é zero.
Exemplo 3: relação cosseno
Suponha que uma variável, X, faça com que a variável Y assuma um valor igual a cos(X).
Por exemplo:
- Se X = -10 então Y = cos(-10) = -0,83907
- Se X = 0 então Y = cos(0) = 1
- Se X = 10 então Y = cos(10) = -0,83907
E assim por diante.
Se traçarmos a relação entre X e Y, ficaria assim:
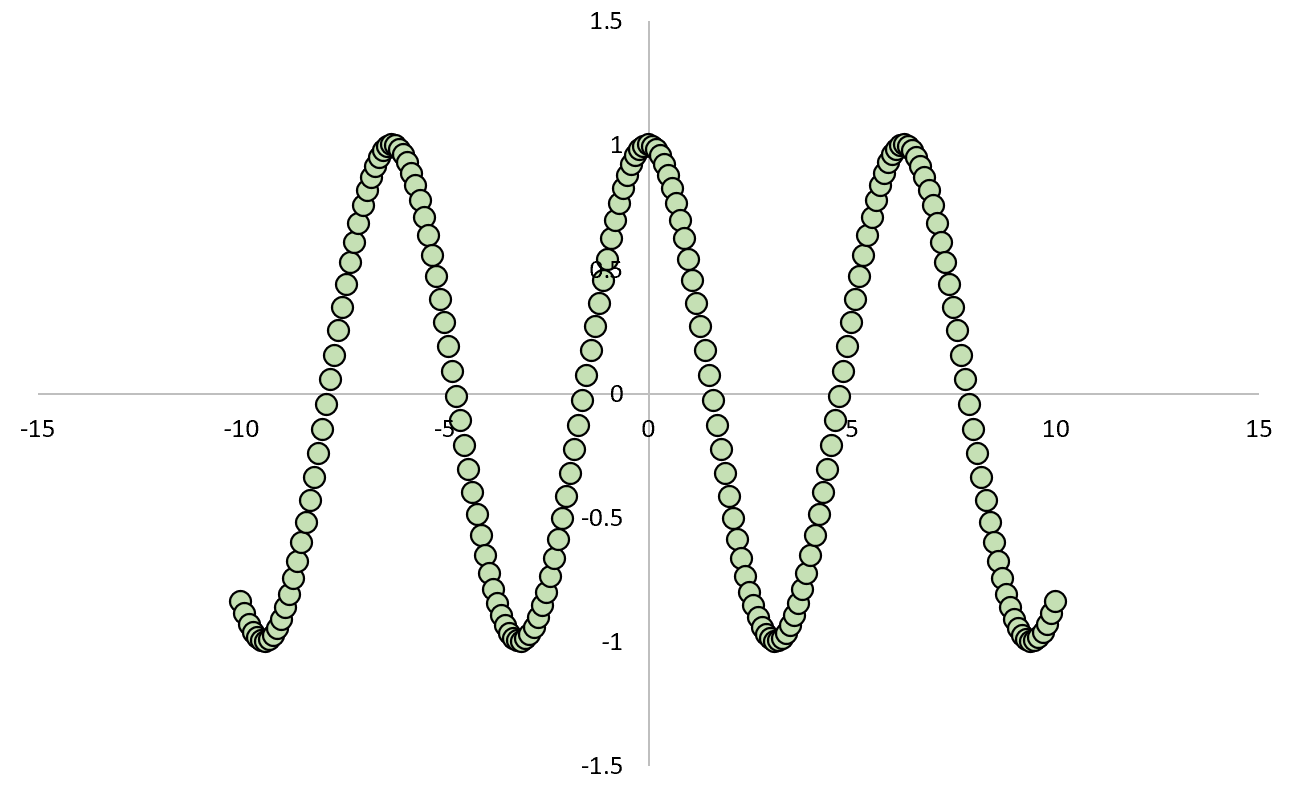
Se calculássemos o coeficiente de correlação de Pearson entre as duas variáveis, descobriríamos que a correlação é zero .
Sabemos que X causa Y, mas a correlação linear entre as duas variáveis é zero.
Recursos adicionais
Os tutoriais a seguir fornecem informações adicionais sobre correlação e causalidade:
Correlação não implica causalidade: 5 exemplos concretos
Introdução ao Coeficiente de Correlação de Pearson
Causalidade reversa: definição e exemplos
About Author
Dr. benjamim anderson
Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais