Como realizar análise bivariada em r (com exemplos)

O termo análise bivariada refere-se à análise de duas variáveis. Você pode se lembrar disso porque o prefixo “bi” significa “dois”.

O objetivo da análise bivariada é compreender a relação entre duas variáveis

Existem três maneiras comuns de realizar análise bivariada:

1. Nuvens de pontos

2. Coeficientes de correlação

3. Regressão linear simples

O exemplo a seguir demonstra como realizar cada um desses tipos de análise bivariada usando o seguinte conjunto de dados que contém informações sobre duas variáveis: (1) Horas gastas estudando e (2) Pontuações em testes obtidas por 20 alunos diferentes:

 #create data frame
df <- data. frame (hours=c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                         3, 4, 4, 5, 5, 6, 6, 6, 7, 8),
                 score=c(75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                         80, 88, 85, 90, 92, 94, 94, 88, 91, 96))

#view first six rows of data frame
head(df)

  hours score
1 1 75
2 1 66
3 1 68
4 2 74
5 2 78
6 2 72

1. Nuvens de pontos

Podemos usar a seguinte sintaxe para criar um gráfico de dispersão de horas estudadas versus nota do exame em R:

 #create scatterplot of hours studied vs. exam score
plot(df$hours, df$score, pch= 16 , col=' steelblue ',
     main=' Hours Studied vs. Exam Score ',
     xlab=' Hours Studied ', ylab=' Exam Score ')

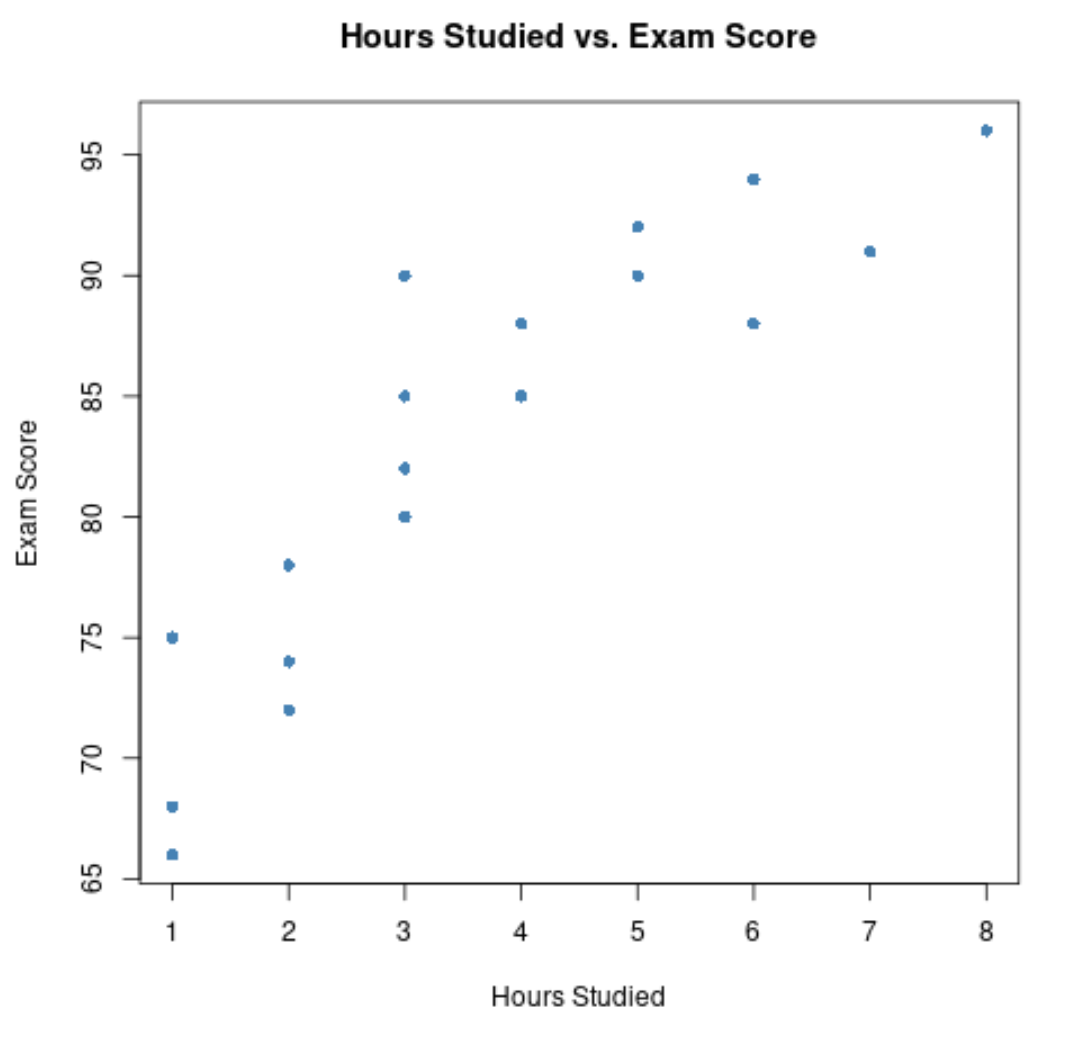
O eixo x mostra as horas estudadas e o eixo y mostra a nota obtida no exame.

O gráfico mostra que existe uma relação positiva entre as duas variáveis: à medida que aumenta o número de horas de estudo, as notas dos exames também tendem a aumentar.

2. Coeficientes de correlação

Um coeficiente de correlação de Pearson é uma forma de quantificar a relação linear entre duas variáveis.

Podemos usar a função cor() em R para calcular o coeficiente de correlação de Pearson entre duas variáveis:

 #calculate correlation between hours studied and exam score received
cor(df$hours, df$score)

[1] 0.891306

O coeficiente de correlação é 0,891 .

Este valor é próximo de 1, indicando uma forte correlação positiva entre as horas estudadas e a nota do exame.

3. Regressão linear simples

A regressão linear simples é um método estatístico que podemos usar para encontrar a equação da reta que melhor “se ajusta” a um conjunto de dados, que podemos então usar para entender a relação exata entre duas variáveis.

Podemos usar a função lm() em R para ajustar um modelo de regressão linear simples para horas estudadas e resultados de exames recebidos:

 #fit simple linear regression model
fit <- lm(score ~ hours, data=df)

#view summary of model
summary(fit)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-6,920 -3,927 1,309 1,903 9,385 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 69.0734 1.9651 35.15 < 2nd-16 ***
hours 3.8471 0.4613 8.34 1.35e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.171 on 18 degrees of freedom
Multiple R-squared: 0.7944, Adjusted R-squared: 0.783 
F-statistic: 69.56 on 1 and 18 DF, p-value: 1.347e-07

A equação de regressão ajustada acaba sendo:

Nota do exame = 69,0734 + 3,8471*(horas estudadas)

Isso nos diz que cada hora adicional estudada está associada a um aumento médio de 3,8471 na nota do exame.

Também podemos usar a equação de regressão ajustada para prever a pontuação que um aluno receberá com base no número total de horas estudadas.

Por exemplo, um aluno que estuda 3 horas deverá obter nota 81,6147 :

• Nota do exame = 69,0734 + 3,8471*(horas estudadas)
• Nota do exame = 69,0734 + 3,8471*(3)
• Resultado do exame = 81,6147

Recursos adicionais

Os tutoriais a seguir fornecem informações adicionais sobre análise bivariada:

Uma introdução à análise bivariada
5 exemplos de dados bivariados na vida real
Uma introdução à regressão linear simples