Como realizar análise bivariada em python: com exemplos

O termo análise bivariada refere-se à análise de duas variáveis. Você pode se lembrar disso porque o prefixo “bi” significa “dois”.

O objetivo da análise bivariada é compreender a relação entre duas variáveis

Existem três maneiras comuns de realizar análise bivariada:

1. Nuvens de pontos

2. Coeficientes de correlação

3. Regressão linear simples

O exemplo a seguir mostra como realizar cada um desses tipos de análise bivariada em Python usando o seguinte DataFrame do pandas que contém informações sobre duas variáveis: (1) Horas gastas estudando e (2) Nota no exame obtida por 20 alunos diferentes:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 1, 1, 2, 2, 2, 3, 3, 3, 3,
                             3, 4, 4, 5, 5, 6, 6, 6, 7, 8],
                   ' score ': [75, 66, 68, 74, 78, 72, 85, 82, 90, 82,
                             80, 88, 85, 90, 92, 94, 94, 88, 91, 96]})

#view first five rows of DataFrame
df. head ()

	hours score
0 1 75
1 1 66
2 1 68
3 2 74
4 2 78

1. Nuvens de pontos

Podemos usar a seguinte sintaxe para criar um gráfico de dispersão de horas estudadas versus resultados de exames:

 import matplotlib. pyplot as plt

#create scatterplot of hours vs. score
plt. scatter (df. hours , df. score )
plt. title (' Hours Studied vs. Exam Score ')
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

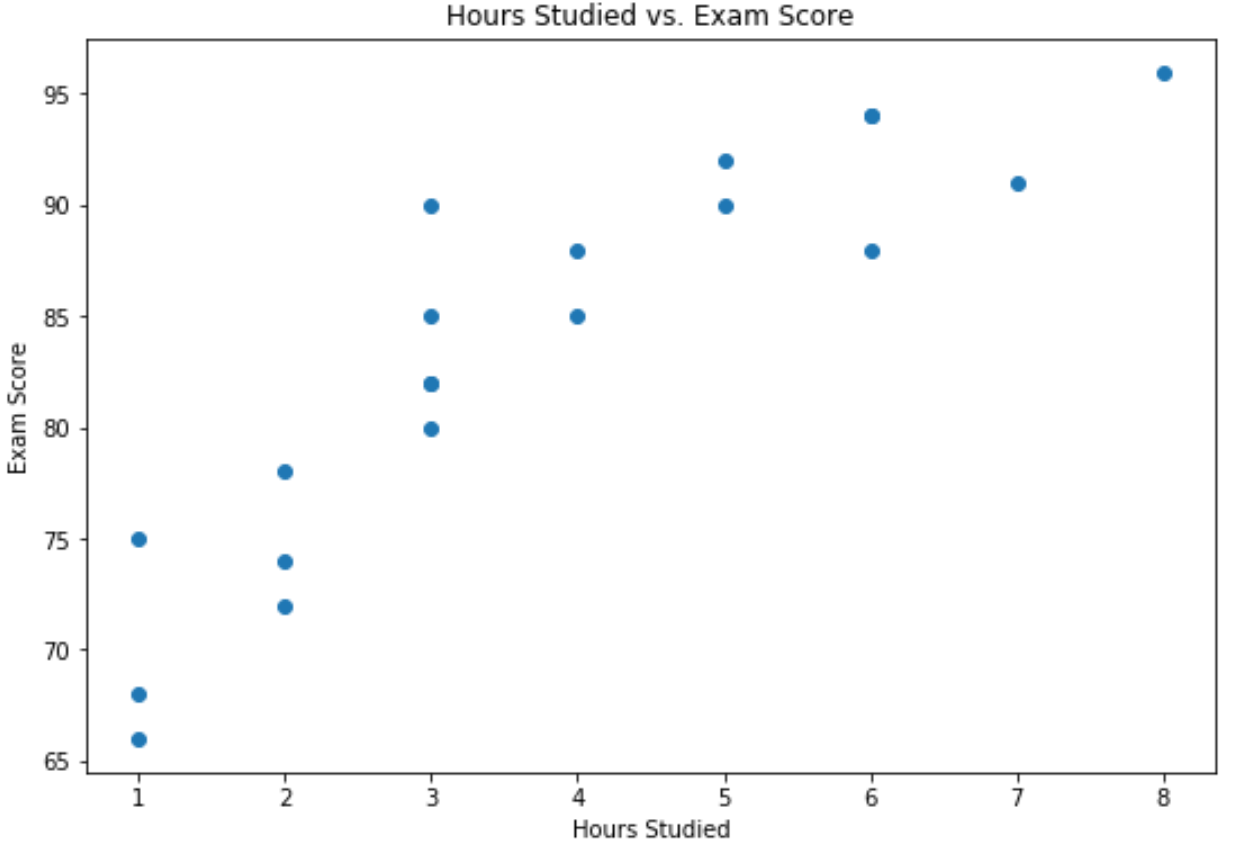
O eixo x mostra as horas estudadas e o eixo y mostra a nota obtida no exame.

O gráfico mostra que existe uma relação positiva entre as duas variáveis: à medida que aumenta o número de horas de estudo, as notas dos exames também tendem a aumentar.

2. Coeficientes de correlação

Um coeficiente de correlação de Pearson é uma forma de quantificar a relação linear entre duas variáveis.

Podemos usar a função corr() em pandas para criar uma matriz de correlação:

 #create correlation matrix
df. corr ()

	hours score
hours 1.000000 0.891306
score 0.891306 1.000000

O coeficiente de correlação é 0,891 . Isso indica uma forte correlação positiva entre horas estudadas e nota no exame.

3. Regressão linear simples

A regressão linear simples é um método estatístico que podemos usar para quantificar a relação entre duas variáveis.

Podemos usar a função OLS() do pacote statsmodels para ajustar rapidamente um modelo de regressão linear simples para horas estudadas e resultados de exames recebidos:

 import statsmodels. api as sm

#define response variable
y = df[' score ']

#define explanatory variable
x = df[[' hours ']]

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.794
Model: OLS Adj. R-squared: 0.783
Method: Least Squares F-statistic: 69.56
Date: Mon, 22 Nov 2021 Prob (F-statistic): 1.35e-07
Time: 16:15:52 Log-Likelihood: -55,886
No. Observations: 20 AIC: 115.8
Df Residuals: 18 BIC: 117.8
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 69.0734 1.965 35.149 0.000 64.945 73.202
hours 3.8471 0.461 8.340 0.000 2.878 4.816
==================================================== ============================
Omnibus: 0.171 Durbin-Watson: 1.404
Prob(Omnibus): 0.918 Jarque-Bera (JB): 0.177
Skew: 0.165 Prob(JB): 0.915
Kurtosis: 2.679 Cond. No. 9.37
==================================================== ============================

A equação de regressão ajustada acaba sendo:

Nota do exame = 69,0734 + 3,8471*(horas estudadas)

Isso nos diz que cada hora adicional estudada está associada a um aumento médio de 3,8471 na nota do exame.

Também podemos usar a equação de regressão ajustada para prever a pontuação que um aluno receberá com base no número total de horas estudadas.

Por exemplo, um aluno que estuda 3 horas deverá obter nota 81,6147 :

• Nota do exame = 69,0734 + 3,8471*(horas estudadas)
• Nota do exame = 69,0734 + 3,8471*(3)
• Resultado do exame = 81,6147

Recursos adicionais

Os tutoriais a seguir fornecem informações adicionais sobre análise bivariada:

Uma introdução à análise bivariada
5 exemplos de dados bivariados na vida real
Uma introdução à regressão linear simples
Uma introdução ao coeficiente de correlação de Pearson