Como realizar manualmente uma anova bidirecional
Uma ANOVA bidirecional é usada para determinar se há ou não uma diferença estatisticamente significativa entre as médias de três ou mais grupos independentes que foram divididos em dois fatores.
Este tutorial explica como realizar manualmente uma ANOVA bidirecional.
Exemplo: ANOVA bidirecional manual
Suponha que um botânico queira saber se o crescimento das plantas é influenciado pela exposição à luz solar e pela frequência de rega. Ela planta 40 sementes e deixa crescer durante um mês em diferentes condições de exposição solar e frequência de rega.
Depois de um mês, ela registra a altura de cada planta. Os resultados são mostrados abaixo:

Na tabela acima vemos que cinco plantas foram cultivadas em cada combinação de condições.
Por exemplo, cinco plantas foram cultivadas com rega diária e sem luz solar e as suas alturas após dois meses eram de 4,8 polegadas, 4,4 polegadas, 3,2 polegadas, 3,9 polegadas e 4,4 polegadas:

Podemos usar as seguintes etapas para realizar uma ANOVA bidirecional:
Passo 1: Calcule a soma dos quadrados para o primeiro fator (frequência de rega)
Primeiro, calcularemos a altura média geral das 40 plantas:
Média geral = (4,8 + 5 + 6,4 + 6,3 +… + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525
A seguir calcularemos a altura média de todas as plantas regadas diariamente:
Média diária = (4,8 + 5 + 6,4 + 6,3 +… + 4,4 + 4,8 + 5,8 + 5,8) /20 = 5,155
A seguir, calcularemos a altura média de todas as plantas regadas a cada semana:
Média semanal = (4,4 + 4,9 + 5,8 + 6 +… + 3,9 + 4,8 + 5,5 + 5,5) /20 = 5,15
A seguir, calcularemos a soma dos quadrados do fator “frequência de rega” usando a seguinte fórmula:
Σn(X j – X ..) 2
Ouro:
- n : o tamanho da amostra do grupo j
- Σ : um símbolo grego que significa “soma”
- X j : a média do grupo j
- X .. : a grande média
No nosso exemplo, calculamos a soma dos quadrados para o fator “frequência de rega” da seguinte forma: 20(5,155-5,1525) 2 + 20(5,15-5,1525) 2 = 0,00025
Passo 2: Calcule a soma dos quadrados para o segundo fator (exposição solar)
Primeiro, calcularemos a altura média geral das 40 plantas:
Média geral = (4,8 + 5 + 6,4 + 6,3 +… + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525
A seguir calcularemos a altura média de todas as plantas não expostas ao sol:
Média sem sol = (4,8 + 4,4 + 3,2 + 3,9 + 4,4 + 4,4 + 4,2 + 3,8 + 3,7 + 3,9) / 10 = 4,07
Repetiremos este cálculo para encontrar a altura média das plantas submetidas a diversas exposições solares:
- Média de baixa insolação = 5,1
- Luz solar média média = 5,89
- Insolação alta média = 5,55
A seguir, calcularemos a soma dos quadrados do fator “exposição solar” usando a seguinte fórmula:
Σn(X j – X ..) 2
Ouro:
- n : o tamanho da amostra do grupo j
- Σ : um símbolo grego que significa “soma”
- X j : a média do grupo j
- X .. : a grande média
Em nosso exemplo, calculamos a soma dos quadrados para o fator “exposição solar” da seguinte forma: 10(4,07-5,1525) 2 + 10(5,1-5,1525) 2 + 10(5,89 -5,1525) 2 + 10(5,55-5,1525) 2 = 18,76475
Etapa 3: Calcule a soma dos quadrados internos (erro)
A seguir, calcularemos a soma dos quadrados tomando a soma dos quadrados das diferenças entre cada combinação de fatores e as alturas individuais das plantas.
Por exemplo, a altura média de todas as plantas regadas diariamente sem exposição solar é 4,14. Podemos então calcular a soma dos quadrados das diferenças para cada uma dessas plantas individuais da seguinte forma:
- SS para rega diária e sem sol: (4,8-4,14) 2 + (4,4-4,14) 2 + (3,2-4,14) 2 + (3,9-4,14) 2 + (4,4-4,14) 2 = 1,512
Podemos repetir esse processo para cada combinação de fatores:
- SS para rega diária e pouca luz solar: 0,928
- SS para rega diária e luz solar média: 1.788
- SS para rega diária e luz solar forte: 1.648
- SS para rega semanal sem sol: 0,34
- SS para rega semanal e pouca luz solar: 0,548
- SS para rega semanal e luz solar média: 0,652
- SS para rega semanal e luz solar forte: 1.268
Podemos então pegar a soma de todos esses valores para encontrar a soma dos quadrados internos (erro):
Somas dos quadrados dentro = 1,512 + 0,928 + 1,788 + 1,648 + 0,34 + 0,548 + 0,652 + 1,268 = 8,684
Etapa 4: Calcule a soma total dos quadrados
Então podemos calcular a soma total dos quadrados tomando a soma das diferenças entre a altura de cada planta e a média geral:
Soma total dos quadrados = (4,8 – 5,1525) 2 + (5 – 5,1525) 2 +… + (5,5 – 5,1525) 2 = 28,45975
Etapa 5: Calcule a interação da soma dos quadrados
A seguir, calcularemos a interação da soma dos quadrados usando a seguinte fórmula:
- Interação SS = SS Total – SS Fator 1 – SS Fator 2 – SS Interior
- Interação SS = 28,45975 – 0,00025 – 18,76475 – 8,684
- Interação SS = 1,01075
Etapa 6: preencha a tabela ANOVA
Por fim, preencheremos os valores da tabela ANOVA bidirecional:
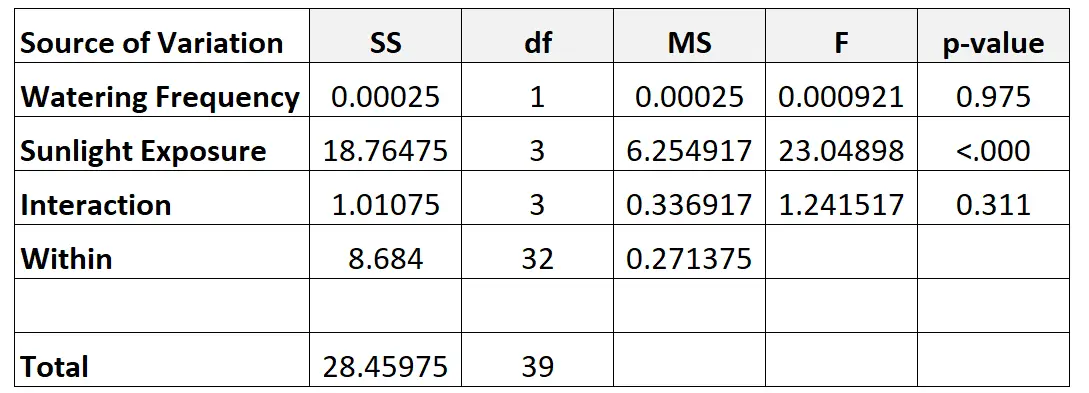
Aqui está como calculamos os diferentes números na tabela:
- df Frequência de rega: d-1 = 2-1 = 1
- df Exposição solar: k-1 = 4-1 = 3
- dfInteração : (j-1)*(k-1) = 1*3 = 3
- df In : n – (j*k) = 40 – (2*4) = 32
- gl total: n-1 = 40-1 = 39
- MS: SS/DF
- Frequência de rega F : frequência de rega interior MS/MS
- F Exposição à luz solar : MS/MS exposição à luz solar em ambientes fechados
- Interação F : Interação MS / MS Dentro
- Valor p frequência de rega : O valor p que corresponde ao valor F de 0,000921 com o numerador df = 1 e o denominador df = 32
- Valor p de exposição solar : o valor p que corresponde ao valor F de 23,04898 com o numerador df = 3 e o denominador df = 32
- interação do valor p : O valor p que corresponde ao valor F de 1,241517 com o numerador df = 3 e o denominador df = 32
Nota #1: n = número total de observações, j = número de níveis para frequência de rega, k = número de níveis para exposição solar.
Nota nº 2 : Os valores p que correspondem ao valor F foram calculados usando a calculadora de distribuição F.
Passo 7: Interprete os resultados
Podemos observar o seguinte na tabela ANOVA:
- O valor p para a interação entre frequência de rega e exposição solar foi de 0,311 . Isto não é estatisticamente significativo em α = 0,05.
- O valor p para frequência de rega foi de 0,975 . Isto não é estatisticamente significativo em α = 0,05.
- O valor de p para exposição solar foi <0,000 . Isto é estatisticamente significativo em α = 0,05.
Estes resultados indicam que a exposição solar é o único fator com efeito estatisticamente significativo na altura das plantas.
E como não existe efeito de interação, o efeito da exposição solar é consistente em cada nível de frequência de rega.
Simplificando, o fato de uma planta ser regada diariamente ou semanalmente não tem impacto sobre como a exposição ao sol afeta a planta.
Recursos adicionais
Os tutoriais a seguir fornecem informações adicionais sobre ANOVAs:
Como realizar manualmente uma ANOVA unidirecional
Como realizar manualmente uma ANOVA de medidas repetidas
O guia completo: como relatar resultados de ANOVA bidirecional