Quase desvio padrão

Este artigo explica o que é o desvio quase padrão nas estatísticas e como ele é calculado. Assim você encontrará a fórmula do desvio quase padrão, um exercício resolvido e, além disso, uma calculadora online para calcular o desvio quase padrão de qualquer conjunto de dados.

O que é desvio quase padrão?

Nas estatísticas, o desvio quase padrão é uma medida de dispersão que indica a variabilidade da amostra. Especificamente, o desvio quase padrão é igual à raiz quadrada da soma dos quadrados dos desvios dividida pelo número total de pontos de dados menos um.

O símbolo para o desvio quase padrão é σ _n-1 os _n-1 .

O desvio quase padrão também pode ser chamado de desvio quase padrão e às vezes também é chamado de desvio padrão amostral, porque geralmente é calculado usando valores de uma amostra estatística. A seguir entraremos em detalhes sobre a diferença entre desvio quase padrão e desvio padrão.

Fórmula de desvio quase padrão

O desvio quase padrão é igual à raiz quadrada da soma dos quadrados dos desvios da série de dados dividida pelo número total de observações menos um. Portanto, a fórmula para calcular o desvio quase padrão é:

Ouro:

• 

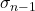
  Este é o desvio quase padrão.

• 

  é o valor dos dados

  

  .

• 

  é o número total de dados.

• 

  é a média do conjunto de dados.

👉 Você pode usar a calculadora abaixo para calcular o desvio quase padrão para qualquer conjunto de dados.

Exemplo de cálculo do desvio quase padrão

Considerando a definição de desvio quase padrão, abaixo você pode ver um exemplo simples de como calcular o desvio quase padrão de um conjunto de dados.

• O orçamento de uma empresa para o seu departamento de investigação e desenvolvimento é muito volátil, porque depende do lucro económico que a empresa obteve no ano anterior. Assim, o orçamento desta secção nos últimos cinco anos foi: 3, 6, 2, 9, 4 milhões de euros. Calcule o desvio quase padrão desta série de dados.

A primeira coisa que precisamos fazer para determinar o desvio quase padrão é calcular a média aritmética da amostra. Para isso, somamos todos os dados e dividimos pelo número total de observações, que é cinco:

A seguir, aplicamos a fórmula do desvio quase padrão:

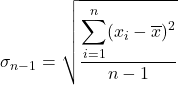
Substituímos os dados na fórmula:

E finalmente calculamos o desvio quase padrão:

Em suma, o quase desvio padrão da amostra de dados é de 2,77 milhões.

Calculadora de desvio quase padrão

Insira um conjunto de dados estatísticos na calculadora online abaixo para calcular seu desvio quase padrão. Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.

Desvio quase padrão e desvio padrão

Por fim, veremos qual é a diferença entre quase desvio padrão e desvio padrão, pois são duas medidas estatísticas diferentes que têm um nome muito semelhante e são calculadas de forma muito semelhante.

A diferença entre o desvio quase padrão e o desvio padrão é o denominador da fórmula. Para calcular o desvio quase padrão, divida por n-1, mas o desvio padrão é calculado dividindo por n.

Portanto, o desvio quase-padrão e o desvio padrão estão matematicamente relacionados, uma vez que o desvio quase-padrão é equivalente ao desvio padrão vezes a raiz quadrada de n (número total de pontos de dados) sobre n-1.

Da equação anterior podemos deduzir que, para o mesmo conjunto de dados, o valor do quase desvio padrão será sempre maior que o valor do desvio padrão.

Além disso, a fórmula do desvio quase padrão é frequentemente usada para calcular o desvio padrão de uma amostra porque elimina vieses. O quase desvio padrão é, portanto, um bom estimador do desvio padrão da população. É por isso que, ao fazer uma inferência estatística a partir de uma amostra, é bastante comum dizer que o desvio padrão é calculado quando na realidade é o desvio quase padrão que é calculado.