Como realizar regressão linear múltipla no sas
A regressão linear múltipla é um método que podemos usar para compreender a relação entre duas ou mais variáveis preditoras e uma variável de resposta .
Este tutorial explica como realizar regressão linear múltipla no SAS.
Etapa 1: crie os dados
Suponha que queiramos ajustar um modelo de regressão linear múltipla que usa o número de horas gastas estudando e o número de exames práticos realizados para prever a nota do exame final dos alunos:
Nota do exame = β 0 + β 1 (horas) + β 2 (exames preparatórios)
Primeiro, usaremos o seguinte código para criar um conjunto de dados contendo essas informações para 20 alunos:
/*create dataset*/ data exam_data; input hours prep_exams score; datalines ; 1 1 76 2 3 78 2 3 85 4 5 88 2 2 72 1 2 69 5 1 94 4 1 94 2 0 88 4 3 92 4 4 90 3 3 75 6 2 96 5 4 90 3 4 82 4 4 85 6 5 99 2 1 83 1 0 62 2 1 76 ; run ;
Etapa 2: realizar regressão linear múltipla
A seguir, usaremos proc reg para ajustar um modelo de regressão linear múltipla aos dados:
/*fit multiple linear regression model*/ proc reg data =exam_data; model score = hours prep_exams; run ;
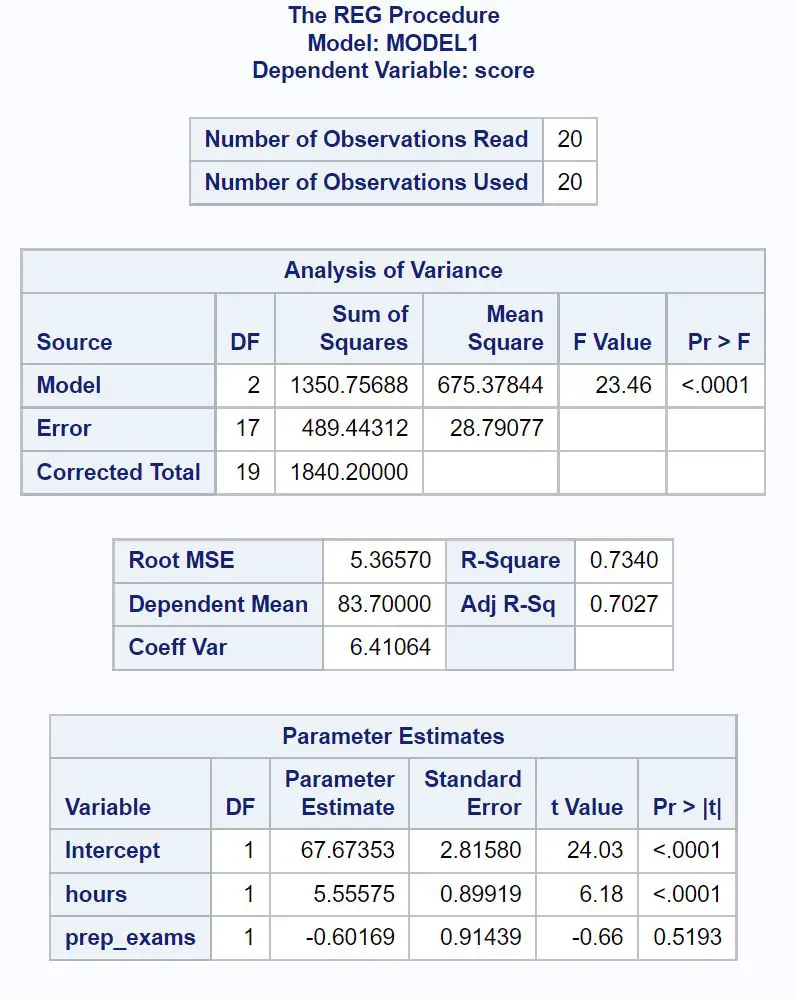
Veja como interpretar os números mais relevantes em cada tabela:
Tabela de análise de lacunas:
O valor F geral do modelo de regressão é 23,46 e o valor p correspondente é <0,0001 .
Como este valor de p é inferior a 0,05, concluímos que o modelo de regressão como um todo é estatisticamente significativo.
Tabela de ajuste do modelo:
O valor R-Square nos diz a porcentagem de variação nas notas dos exames que pode ser explicada pelo número de horas estudadas e pelo número de exames preparatórios realizados.
Em geral, quanto maior o valor R-quadrado de um modelo de regressão, melhores serão as variáveis preditoras em prever o valor da variável resposta.
Neste caso, 73,4% da variação nas notas dos exames pode ser explicada pelo número de horas estudadas e pelo número de exames preparatórios realizados.
O valor Root MSE também é útil saber. Isto representa a distância média entre os valores observados e a linha de regressão.
Neste modelo de regressão, os valores observados desviam-se em média 5,3657 unidades da reta de regressão.
Tabela de estimativas de parâmetros:
Podemos usar os valores estimados dos parâmetros nesta tabela para escrever a equação de regressão ajustada:
Nota do exame = 67,674 + 5,556*(horas) – 0,602*(prep_exams)
Podemos usar esta equação para encontrar a pontuação estimada de um aluno no exame, com base no número de horas de estudo e no número de exames práticos que ele fez.
Por exemplo, um aluno que estuda 3 horas e faz 2 exames preparatórios deverá receber nota 83,1 no exame:
Nota estimada do exame = 67,674 + 5,556*(3) – 0,602*(2) = 83,1
O valor p para horas (<0,0001) é menor que 0,05, o que significa que tem associação estatisticamente significativa com o resultado do exame.
Contudo, o valor p dos exames preparatórios (0,5193) não é inferior a 0,05, o que significa que não tem associação estatisticamente significativa com o resultado do exame.
Podemos decidir retirar os exames preparatórios do modelo, por não serem estatisticamente significativos, e em vez disso realizaruma regressão linear simples usando as horas estudadas como única variável preditora.
Recursos adicionais
Os tutoriais a seguir explicam como executar outras tarefas comuns no SAS:
Como calcular a correlação no SAS
Como realizar regressão linear simples no SAS
Como realizar ANOVA unidirecional no SAS