Teste de hipótese para proporção

By Dr. benjamim anderson Agosto 3, 2023 Estatisticas 0 Comments

Este artigo explica o que é o teste de hipótese de proporção nas estatísticas. Você encontrará, portanto, a fórmula do teste de hipótese da proporção e, além disso, um exercício passo a passo para entender perfeitamente como isso é feito.

O que é teste de hipótese para proporção?

O teste de hipótese de proporção é um método estatístico usado para determinar se deve ou não rejeitar a hipótese nula de uma proporção populacional.

Assim, dependendo do valor da estatística do teste de hipótese para a proporção e o nível de significância, a hipótese nula é rejeitada ou aceita.

Observe que o teste de hipótese também pode ser chamado de contraste de hipótese, teste de hipótese ou teste de significância.

Fórmula de teste de hipóteses para proporção

A estatística do teste de hipótese para a proporção é igual à diferença na proporção da amostra menos o valor proposto da proporção dividido pelo desvio padrão da proporção.

A fórmula da hipótese de teste para a proporção é, portanto:

$\displaystyle Z=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}$

Ouro:

$Z$

é a estatística do teste de hipótese para a proporção.
$\widehat{p}$

é a proporção da amostra.
$p$

é o valor da proporção proposta.
$n$

é o tamanho da amostra.
$\displaystyle\sqrt{\frac{p(1-p)}{n}}$

é o desvio padrão da proporção.

Tenha em mente que não basta calcular a estatística do teste de hipótese para a proporção, mas o resultado deve então ser interpretado:

Se o teste de hipótese para a proporção for bilateral, a hipótese nula é rejeitada se o valor absoluto da estatística for maior que o valor crítico Z _α/2 .
Se o teste de hipótese para a proporção corresponder à cauda direita, a hipótese nula é rejeitada se a estatística for maior que o valor crítico Z _α .
Se o teste de hipótese para a proporção corresponder à cauda esquerda, a hipótese nula é rejeitada se a estatística for menor que o valor crítico -Z _α .

$\begin{array}{l}H_1: p\neq p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: p> p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: p< p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}$

Lembre-se de que os valores críticos podem ser facilmente obtidos na tabela de distribuição normal.

➤ Veja: Tabela de distribuição normal

Exemplo de teste de hipóteses para proporção

Assim que vermos a definição de teste de hipótese para proporção e qual é sua fórmula, resolveremos um exemplo para entender melhor o conceito.

Segundo o fabricante, um medicamento contra uma doença específica tem 70% de eficácia. Em laboratório testamos a eficácia desse medicamento, pois os pesquisadores acreditam que a proporção é diferente. Para isso, o medicamento é testado em uma amostra de 1.000 pacientes e 641 pessoas são curadas. Realizar um teste de hipótese sobre a proporção populacional com nível de significância de 5% para rejeitar ou não a hipótese dos pesquisadores.

Neste caso, a hipótese nula e a hipótese alternativa do teste de hipótese para a proporção populacional são:

$\begin{cases}H_0: p=0,70\\[2ex] H_1:p\neq 0,70 \end{cases}$

A proporção de pessoas na amostra que foram curadas pelo medicamento é:

$\widehat{p}=\cfrac{641}{1000}=0,641$

Calculamos a estatística do teste de hipótese para a proporção aplicando a fórmula vista acima:

$\begin{aligned} \displaystyle Z&=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}\\[2ex]Z&=\frac{0,641-0,70}{\displaystyle\sqrt{\frac{0,70\cdot (1-0,70)}{1000}}} \\[2ex] Z&=-4,07\end{aligned}}$

Por outro lado, como o nível de significância é 0,05 e este é um teste de hipótese bicaudal, o valor crítico do teste é 1,96.

$Z_{0,025}=1,96$

➤ Veja: Nível de significância 0,05

Concluindo, o valor absoluto da estatística de teste é maior que o valor crítico, portanto rejeitamos a hipótese nula e aceitamos a hipótese alternativa.

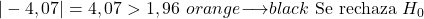$|-4,07|=4,07>1,96 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_0″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”424″ style=”vertical-align: -5px;”></p> </p> <div style=$ ➤ Veja: Teste de hipótese para a média

Teste de hipóteses para duas proporções amostrais

O teste de hipóteses para proporções de duas amostras é usado para rejeitar ou aceitar a hipótese nula de que as proporções de duas populações diferentes são iguais.

Assim, a hipótese nula de um teste de hipótese para proporções de duas amostras é sempre:

$H_0: p_1=p_2$

Embora a hipótese alternativa possa ser uma das três opções:

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}H_1:p_1\neq p_2\\[2ex]H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio of the two samples is calculated as follows:[latex]p=\cfrac {x_1+x_2}{n_1+n_2}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ...H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio
Please use \mathaccent for accents in math mode.
leading text: ...\[2ex]H_1:p_1 The combined ratio of the two
Please use \mathaccent for accents in math mode.
leading text: ...combined of the two samples is calculated
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.

E a fórmula para calcular a estatística do teste de hipótese para duas proporções amostrais é:

$\displaystyle Z=\frac{\displaystyle \frac{x_1}{n_1}-\frac{x_2}{n_2}}{\displaystyle \sqrt{p(1-p)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}$

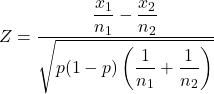
Ouro:

$Z$

é a estatística do teste de hipótese para proporções de duas amostras.
$x_1$

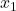
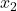
é o número de resultados na amostra 1.
$x_2$

é o número de resultados na amostra 2.
$n_1$

é o tamanho da amostra 1.
$n_2$

é o tamanho da amostra 2.
$p$

é a proporção combinada das duas amostras.

Teste de hipóteses para k proporções de amostras

Num teste de hipótese sobre proporções de k amostras, o objetivo é determinar se todas as proporções das diferentes populações são iguais ou, pelo contrário, se existem proporções diferentes. Portanto, a hipótese nula e a hipótese alternativa neste caso são:

$\begin{cases}H_0: \text{Todas las proporciones son iguales}\\[2ex] H_1: \text{No todas las proporciones son iguales} \end{cases}$

Neste caso, a proporção combinada de todas as amostras é calculada da seguinte forma:

$p=\cfrac{\displaystyle\sum_{i=1}^k x_i}{\displaystyle\sum_{i=1}^k n_i}=\cfrac{x_1+x_2+\dots+x_k}{n_1+n_2+\dots+n_k}$

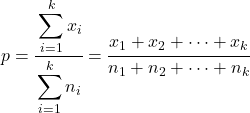
A fórmula para encontrar a estatística do teste de hipótese para k proporções amostrais é:

$\displaystyle \chi^2 =\sum_{i=1}^k \frac{(x_i-e_i)^2}{e_i}$

$\displaystyle\chi^2 = \frac{(x_1-e_1)^2}{e_1} +\frac{(x_2-e_2)^2}{e_2} +\dots+\frac{(x_k-e_k)^2}{e_k}$

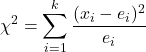
Ouro:

$\chi^2$

é a estatística do teste de hipótese para k proporções amostrais. Nesse caso, a estatística segue uma distribuição qui-quadrado.
$x_i$

é o número de resultados na amostra i.
$n_i$

é o tamanho da amostra i.
$p$

é a proporção combinada de todas as amostras.
$e_i$

é o número de acertos esperados da amostra i. É calculado multiplicando a proporção combinada

$p$

por tamanho de amostra

$n_i$

.

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais

O que é teste de hipótese para proporção?

Fórmula de teste de hipóteses para proporção

Exemplo de teste de hipóteses para proporção

Teste de hipóteses para duas proporções amostrais

Teste de hipóteses para k proporções de amostras

About Author

Dr. benjamim anderson

Add a Comment