Teste de hipótese para variância

By Dr. benjamim anderson Agosto 3, 2023 Estatisticas 0 Comments

Este artigo explica o que é teste de hipótese de variância. Assim, você encontrará a fórmula para teste de hipóteses de variância e, além disso, um exercício resolvido passo a passo.

O que é teste de hipótese para variância?

O teste de hipóteses para variância é um método estatístico usado para determinar se deve ou não rejeitar a hipótese nula de uma variância populacional. Em outras palavras, o teste de hipótese de variância é usado para rejeitar ou aceitar a hipótese sobre o valor da variância de uma população.

Especificamente, dependendo do valor da estatística do teste de hipótese para variância e do nível de significância escolhido, a hipótese nula é rejeitada ou aceita.

Tenha em mente que o teste de hipótese tem vários nomes; também pode ser chamado de contraste de hipótese, teste de hipótese ou teste de significância.

Fórmula de teste de hipóteses para variância

A estatística do teste de hipótese para variância é igual à diferença entre o tamanho da amostra menos uma vez a variância da amostra e dividida pelo valor proposto da variância populacional. A estatística do teste de hipótese para variância tem uma distribuição qui-quadrado .

Assim, a fórmula para cálculo da estatística do teste de hipótese para variância é a seguinte:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Ouro:

$\chi^2$

é a estatística de teste de hipótese para variância, que tem uma distribuição qui-quadrado.
$n$

é o tamanho da amostra.
$s^2$

é a variância da amostra.
$\sigma^2$

é a variância populacional proposta.

Para interpretar o resultado da estatística, o valor obtido deve ser comparado com o valor crítico do teste.

Se o teste de hipótese de variância for bicaudal, a hipótese nula será rejeitada se a estatística for maior que o valor crítico.
$\chi_{1-\alpha/2|n-1}^2$

ou se o valor crítico for menor que

$\chi_{\alpha/2|n-1}$

.
Se o teste de hipótese para a variância corresponder à cauda direita, a hipótese nula será rejeitada se a estatística for maior que o valor crítico
$\chi_{1-\alpha|n-1}^2$

.
Se o teste de hipótese para variância corresponder à cauda esquerda, a hipótese nula será rejeitada se a estatística for menor que o valor crítico
$\chi_{\alpha|n-1}$

.

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

Os valores críticos do teste de hipótese para variância são obtidos na tabela de distribuição qui-quadrado. Observe que os graus de liberdade para a distribuição qui-quadrado são o tamanho da amostra menos 1.

Exemplo do mundo real de teste de hipóteses para variância

Depois de ver a definição de teste de hipótese de variância e qual é sua fórmula, veremos um exemplo concreto para finalizar a assimilação do conceito.

Uma fábrica possui uma máquina que produz peças para um carro com alta precisão. Porém, suspeita-se que tenha se afastado e agora fabrique peças com folga superior a 8 mm ² . Para refutar esta hipótese, uma amostra de 25 peças é analisada e sua variância amostral é de 9,1 mm ² . A hipótese inicial pode ser rejeitada com nível de significância α=0,05?

A hipótese nula e a hipótese alternativa para este teste de hipótese de variância são as seguintes:

$\begin{cases}H_0: \sigma^2=8 \\[2ex] H_1:\sigma^2>8 \end{cases}” title=”Rendered by QuickLaTeX.com” height=”65″ width=”101″ style=”vertical-align: 0px;”> Para determinar se a hipótese nula pode ou não ser rejeitada, calculamos a estatística do teste de hipótese para a variância usando a fórmula que vimos acima: <p class=$ $\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

$\chi^2=\cfrac{(25-1)\cdot 9,1}{8}$

$\chi^2=27,3$

Procuramos agora o valor crítico correspondente à cauda direita para 24 graus de liberdade e um nível de significância α=0,05 na tabela de distribuição qui-quadrado:

$\begin{array}{c}\chi^2_{1-\alpha|n-1}=\ \color{orange}\bm{?}\color{black}\\[2ex]\chi^2_{0,95|24}=36,415\end{array}$

Assim, a estatística calculada é inferior ao valor crítico do teste e, portanto, a hipótese nula do teste de hipótese de variância não é rejeitada, mas sim a hipótese alternativa é rejeitada.

$27,3<36,415 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{No se rechaza } H_0$

➤ Veja: Teste de hipótese para a média populacional
➤ Veja: Teste de hipóteses para proporção populacional

Teste de hipóteses para variância de duas populações

O teste de hipótese de variância de duas populações é usado para rejeitar ou aceitar a hipótese de que as variâncias de duas populações diferentes são iguais.

Assim, a hipótese nula de um teste de hipótese sobre a variância de duas populações é sempre a seguinte:

$H_0: \sigma^2_1=\sigma^2_2$

E a hipótese alternativa pode ser uma das três opções:

$\begin{array}{l}H_1:\sigma^2_1\neq \sigma^2_2\\[2ex]H_1:\sigma^2_1>\sigma^2_2\\[2ex]H_1:\sigma^2_1<\sigma^2_2\end{array}$

Neste caso, a fórmula para calcular a estatística do teste de hipótese para a variância de duas populações é:

$F=\cfrac{s_1^2}{s_2^2}$

Ouro:

$F$

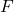
é a estatística de teste de hipótese para a variância de duas populações, que segue uma distribuição F.
$\sigma_1^2$

é a variância da população 1.
$\sigma_2^2$

é a variância da população 2.
$s_1^2$

é a variância da amostra 1.
$s_2^2$

é a variância da amostra 2.
$n_1$

é o tamanho da amostra 1.
$n_2$

é o tamanho da amostra 2.

Como a distribuição Snedecor F não é simétrica, a hipótese nula é rejeitada com base nos seguintes critérios:

[látex]\begin{array}{l}H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F>F_{ 1-\alpha/2|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow }\cor{preto} \ \text{If }F \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{If } F>F_{1-\alpha|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2< \sigma_2^2 \ \color{laranja}\bm{\longrightarrow}\color{preto} \ \text{Si } F

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais