População significa

By Dr. benjamim anderson Agosto 3, 2023 Estatisticas 0 Comments

Este artigo explica o que população significa nas estatísticas. Da mesma forma, você descobrirá qual é a fórmula da média populacional, como é calculado o intervalo de confiança da média populacional e, além disso, qual a diferença entre a média populacional e a média da amostra.

Qual é a média da população?

A média da população é a média aritmética de todos os elementos da população estatística. Portanto, para calcular a média populacional, todos os valores populacionais devem ser somados e depois divididos pelo número total de elementos da população.

O símbolo da média populacional é a letra grega μ.

Da mesma forma, a média populacional também pode ser definida como o valor esperado da variável que representa uma população.

Como calcular a média populacional

Depois de vermos a definição de média populacional, vamos ver como a média populacional é calculada para entender melhor seu significado.

Se todos os valores da população estatística forem conhecidos, a fórmula da média aritmética deve ser simplesmente aplicada para calcular a média populacional. Portanto, neste caso, para calcular a média populacional, precisamos somar todos os valores populacionais e depois dividir pelo número total de dados.

Assim, se conhecermos o valor de todos os elementos da população, a fórmula para calcular a média populacional é a seguinte:

$\displaystyle\mu=\frac{\displaystyle \sum_{i=1}^N x_i}{N}=\frac{x_1+x_2+\dots +x_N}{N}$

➤ Veja: Exemplo de cálculo da média aritmética

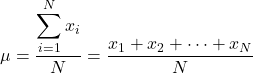
Porém, em geral nem todos os valores populacionais são conhecidos, então normalmente o valor da média populacional é estimado por intervalos .

Intervalo de confiança para média populacional

Na prática, é impossível estudar todos os indivíduos de uma população, por isso normalmente escolhe-se uma amostra aleatória da população e, com base nos seus valores, faz-se uma aproximação do valor da média populacional. Mais precisamente, calculamos um intervalo no qual é muito provável que se encontre a média de toda a população; esse intervalo é chamado de intervalo de confiança para a média populacional.

O intervalo de confiança para a média populacional é calculado somando e subtraindo da média amostral o valor de Z _α/2 multiplicado pelo desvio padrão (σ) e dividido pela raiz quadrada da altura da amostra (n). Portanto, a fórmula para cálculo do intervalo de confiança para a média populacional é:

$\displaystyle \left(\overline{x}-z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \ , \ \overline{x}+z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \right)$

A fórmula acima é usada quando a variância populacional é conhecida. Porém, se a variância populacional for desconhecida, que é o caso mais comum, o intervalo de confiança para a média é calculado utilizando a seguinte fórmula:

$\displaystyle \left(\overline{x}-t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \ , \ \overline{x}+t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \right)$

Ouro:

$\overline{x}$

é a média amostral.
$t_{\alpha/2}$

é o valor da distribuição t de Student de n-1 graus de liberdade com probabilidade α/2. Para amostras grandes e nível de confiança de 95% é geralmente próximo de 1,96 e para nível de confiança de 99% é geralmente próximo de 2,576.
$s$

é o desvio padrão da amostra.
$n$

é o tamanho da amostra.

➤ Veja: Exemplo de cálculo do intervalo de confiança para a média populacional

Média populacional e média amostral

Finalmente, em resumo, revisaremos as diferenças entre a média populacional e a média amostral para que esses dois conceitos estatísticos fiquem claros.

A diferença entre a média populacional e a média amostral é o intervalo de valores sobre o qual a média é calculada. A média da população é a média de toda a população estatística, enquanto a média da amostra é a média de uma amostra da população.

Além disso, para diferenciar a média populacional da média amostral, elas são representadas por símbolos diferentes. O símbolo para a população significa é

$\mu$

, por outro lado, o símbolo para as médias amostrais é

$\overline{x}$

$\begin{array}{c}\mu =\text{Media poblacional}\\[2ex]\overline{x} = \text{Media muestral}\end{array}$

Se ainda tiver dúvidas sobre as diferenças entre estes dois tipos de médias ou quiser saber mais sobre como calcular a média amostral, pode consultar o seguinte artigo:

➤ Veja: Qual é a média da amostra?

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais