Como encontrar a variação de dados agrupados (com exemplo)

Muitas vezes queremos calcular a variância de uma distribuição de frequência agrupada.

Por exemplo, suponha que temos a seguinte distribuição de frequência agrupada:

Embora não seja possível calcular a variância exata, pois não conhecemos os valores dos dados brutos , é possível estimar a variância usando a seguinte fórmula:

Variância: Σn _i (m _i -μ) ² / (N-1)

Ouro:

• n _i : A frequência do i- ^ésimo grupo
• _mi : O meio do i- ^ésimo grupo
• μ : A média
• N: O tamanho total da amostra

Nota: O ponto médio de cada grupo pode ser encontrado calculando a média dos valores inferior e superior do intervalo. Por exemplo, o ponto médio do primeiro grupo é calculado da seguinte forma: (1+10) / 2 = 5,5.

O exemplo a seguir mostra como usar esta fórmula na prática.

Exemplo: Calcular a variação de dados agrupados

Suponha que temos os seguintes dados agrupados:

Veja como usaríamos a fórmula mencionada anteriormente para calcular a variação desses dados agrupados:

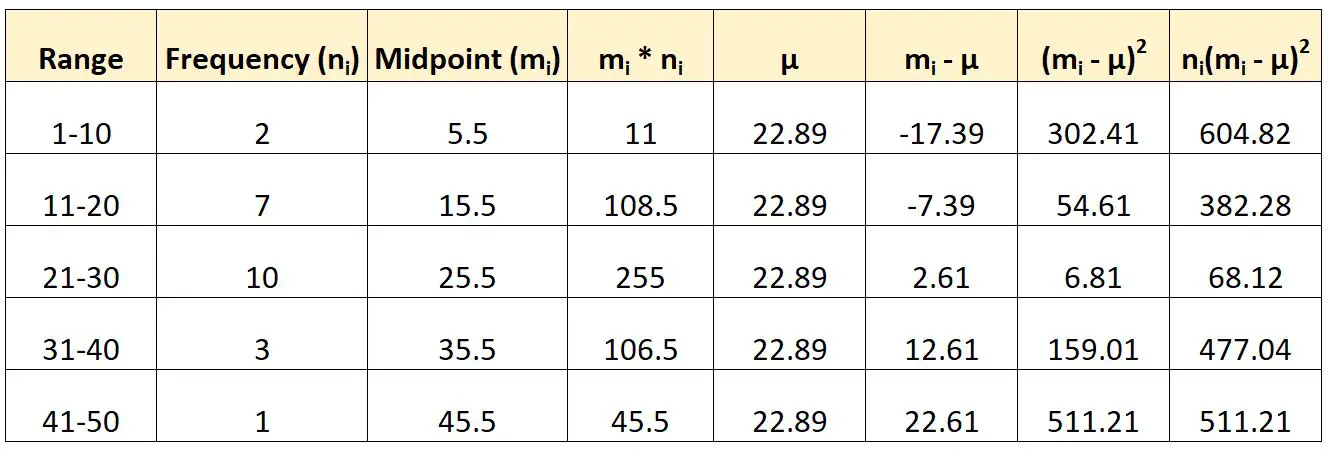
Calcularíamos então a variância da seguinte forma:

• Variância: Σn _i (m _i -μ) ² / (N-1)
• Diferença : (604,82 + 382,28 + 68,12 + 477,04 + 511,21) / (23-1)
• Diferença : 92.885

A variação do conjunto de dados é 92.885 .

Recursos adicionais

Os tutoriais a seguir explicam como calcular outras métricas para dados agrupados:

Como encontrar a média e o desvio padrão de dados agrupados
Como calcular a classificação percentil para dados agrupados
Como encontrar a mediana de dados agrupados
Como encontrar o modo de dados agrupados