Distribuição amostral de diferença de médias

By Agosto 3, 2023 Estatisticas 0 Comments

Este artigo explica o que é a distribuição amostral da diferença entre duas médias nas estatísticas. Você também encontrará a fórmula de distribuição amostral da diferença de médias e, além disso, um exercício resolvido passo a passo.

Qual é a distribuição amostral da diferença de médias?

A distribuição amostral da diferença de médias é a distribuição que resulta do cálculo das diferenças entre as médias de todas as amostras possíveis de duas populações diferentes.

Ou seja, para obter a distribuição amostral da diferença de médias, devem ser selecionadas todas as amostras possíveis de duas populações de estudo, em seguida é calculada a média de cada amostra selecionada e, por fim, calculada a diferença entre todas as médias das duas populações. Assim, o conjunto de valores obtidos após a aplicação de todas essas operações forma a distribuição amostral da diferença de médias.

distribuição amostral de diferença de médias

A diferença de distribuição amostral de médias é usada para calcular a probabilidade de que a diferença entre duas médias de amostras selecionadas aleatoriamente de duas populações diferentes esteja próxima da diferença nas médias populacionais.

Fórmula para a distribuição amostral da diferença de médias

Se o tamanho da amostra for grande o suficiente (n 1 ≥30 e n 2 ≥30), a distribuição amostral da diferença nas médias segue uma distribuição normal. Mais precisamente, os parâmetros desta distribuição são calculados da seguinte forma:

\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}

Nota: Se ambas as populações forem distribuições normais , então a distribuição amostral da diferença nas médias segue uma distribuição normal, independentemente do tamanho da amostra.

Portanto, como a distribuição amostral da diferença de médias é definida por uma distribuição normal, a fórmula para calcular a estatística da distribuição amostral da diferença de médias é:

Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}

Ouro:

  • \overline{x_i}

    é a média da amostra i.

  • \mu_i

    é a média da população i.

  • \sigma_i

    é o desvio padrão da população i.

  • n_i

    é o tamanho da amostra i.

  • Z

    é uma variável definida pela distribuição normal padrão N(0,1).

Observe que amostras de populações diferentes podem ter tamanhos de amostra diferentes.

Exemplo concreto de distribuição amostral da diferença de médias

Depois de vermos a definição de distribuição amostral por diferença de médias e qual é sua fórmula, veremos um exemplo passo a passo para finalizar a compreensão do conceito de distribuição amostral por diferença de médias.

  • Num estudo estatístico, queremos analisar a diferença entre a altura de meninos e meninas de uma determinada idade. Sabemos que a distribuição que define a população de meninos desta idade tem média de 157 cm e desvio padrão de 9 cm e, por outro lado, a distribuição que define a população de meninas desta idade tem média de 148 cm e um desvio padrão de 7 cm. Se forem selecionadas uma amostra de 30 meninos desta idade e uma amostra de 35 meninas desta idade, qual é a probabilidade de a altura média da amostra de meninos ser 12 cm maior que a altura média da amostra de meninas?

Para resolver este problema, a primeira coisa a fazer é calcular a estatística da diferença de médias da distribuição amostral. Portanto, aplicamos a fórmula vista acima:

Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right)}=\cfrac{12-(157-148)}{\displaystyle\sqrt{\frac{9^2}{30}+\frac{7^2}{35}}}=1,48

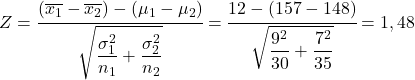
Portanto, a probabilidade de a altura média amostral dos meninos ser 12 cm maior que a altura média das meninas equivale à probabilidade de a variável Z ser maior que 1,48.

P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”253″ style=”vertical-align: -5px;”></p> </p> <p> Procuramos, portanto, a probabilidade de Z>1,48 na <a href=tabela de Z :

P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]=0,0694″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”331″ style=”vertical-align: -5px;”></p> </p> <p> Em suma, a probabilidade de a altura média amostral dos meninos ser 12 cm maior que a altura média das meninas é de 6,94%.</p> </div><!-- End Content --> <!-- Start Author Box --> <div class=

About Author

Dr. Benjamin Anderson
Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais

Add a Comment

O seu endereço de email não será publicado. Campos obrigatórios marcados com *