Por que a moda é importante nas estatísticas?
A moda representa o valor que aparece com mais frequência em um conjunto de dados.
Um conjunto de dados não pode ter modos (se nenhum valor se repetir), um modo ou vários modos.
Por exemplo, a moda no seguinte conjunto de dados é 19:
Conjunto de dados: 3, 4, 11, 15, 19 , 19, 19 , 22 , 22, 23, 23, 26
Este é o valor que aparece com mais frequência.
Nas estatísticas, a moda é importante pelos seguintes motivos:
Razão 1 : isso nos permite saber quais valores em um conjunto de dados são os mais comuns.
Razão 2 : É útil para encontrar o valor mais frequente em dados categóricos quando a média e a mediana não podem ser calculadas.
Razão 3 : nos dá uma ideia de onde está o “centro” de um conjunto de dados, embora a mediana e a média sejam mais comumente usadas (como veremos mais adiante neste artigo).
Os exemplos a seguir ilustram cada uma dessas razões na prática.
Razão 1: o modo nos diz qual valor é mais comum
Digamos que temos um conjunto de dados de 100.000 linhas contendo os preços de venda de casas nos Estados Unidos:

Suponha que usamos software estatístico (como Excel , R , Python , etc.) para calcular a moda deste conjunto de dados e descobrimos que existem três modos:
- US$ 280.000
- US$ 300.000
- US$ 305.000
Isto dá-nos imediatamente uma ideia dos preços das casas mais comuns no conjunto de dados.
Calcular a moda dos milhares também é muito mais rápido do que observar linhas de dados e tentar identificar quais preços de casas ocorrem com mais frequência.
Razão 2: o modo procura o valor mais comum em dados categóricos
Suponha que temos um conjunto de dados de 1.000 linhas que nos informa a cor do carro de propriedade de indivíduos em um determinado bairro:
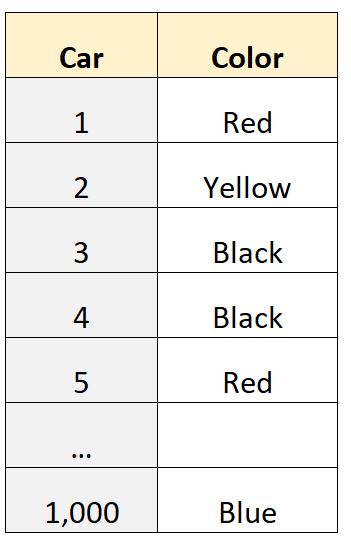
A variável “cor” é uma variável categórica , o que significa que os valores pertencem a categorias (“vermelho”, “amarelo”, “preto”, etc.) e portanto não podemos calcular um valor quantitativo como a média ou a mediana .
No entanto, podemos calcular a moda porque ela simplesmente representa o valor mais comum no conjunto de dados.
Por exemplo, poderíamos usar software estatístico para determinar que o modo deste conjunto de dados é “preto”, o que nos diz que a cor de carro mais comum neste conjunto de dados é preto.
Razão 3: o modo nos dá uma ideia de onde está o centro de um conjunto de dados
A moda também é considerada uma medida de tendência central , o que significa que pode nos dar uma ideia de onde está o “centro” do conjunto de dados.
Por exemplo, suponha que temos o seguinte conjunto de dados que mostra as notas dos exames de 20 alunos diferentes em uma turma:

A moda é 82 – esta é a pontuação mais comum no exame. Isso também acaba sendo uma boa indicação de onde está o valor da pontuação de revisão “principal” neste conjunto de dados.
No entanto, suponha que tenhamos o seguinte conjunto de dados de resultados de exames:
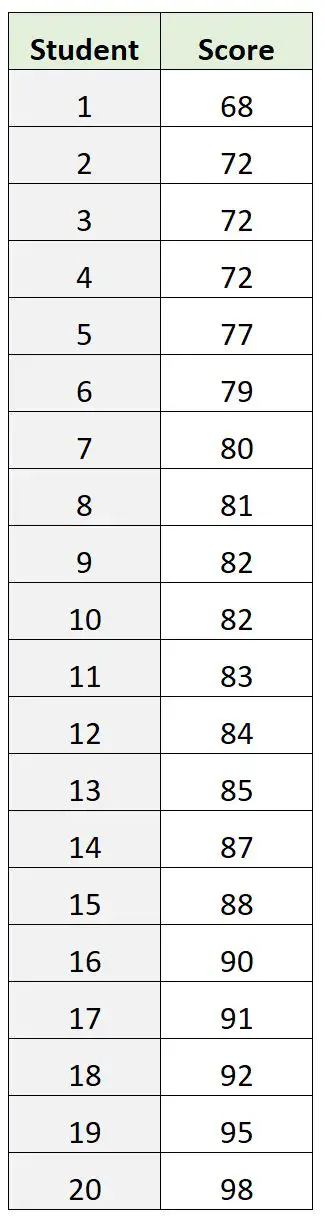
Neste conjunto de dados, 72 é a pontuação do exame de moda. No entanto, isso acaba sendo uma má indicação de onde está a pontuação “principal” do exame.
A nota média do exame é 82,9 e a nota mediana do exame é 82,5 , ambas nos dando uma ideia melhor de onde está o valor “central” em relação à moda.
Resumo
Aqui está um breve resumo dos principais pontos abordados neste artigo:
- A moda representa o(s) valor(es) que aparecem com mais frequência em um conjunto de dados.
- A moda nos informa o valor mais comum em dados categóricos quando a média e a mediana não podem ser usadas.
- A moda nos dá uma ideia de onde está o “centro” de um conjunto de dados, mas pode ser enganosa quando comparada à média ou mediana.
Recursos adicionais
Os tutoriais a seguir fornecem informações adicionais sobre média, mediana e moda em estatísticas:
Por que a média é importante nas estatísticas?
Por que a mediana é importante nas estatísticas?
Exemplos concretos: usando média, mediana e moda
Quando usar média vs. Mediana: com exemplos