Teste de hipóteses para diferença de médias

By Dr. benjamim anderson Agosto 3, 2023 Estatisticas 0 Comments

Este artigo explica o que é o teste de hipótese de diferença de médias nas estatísticas e para que ele é usado. Da mesma forma, você descobrirá como fazer um teste de hipótese sobre a diferença de médias e um exercício resolvido passo a passo.

O que é teste de hipótese para diferença média?

O teste de hipóteses para diferença de médias é um teste estatístico usado para rejeitar ou aceitar a hipótese de que as médias de duas populações são diferentes. Ou seja, o teste de hipótese de diferença de médias é usado para determinar se as médias de duas populações são iguais ou diferentes.

Tenha em mente que as decisões tomadas em testes de hipóteses são baseadas em um nível de confiança previamente estabelecido, portanto não se pode garantir que o resultado de um teste de hipóteses esteja sempre correto, mas sim que é o resultado mais provável que seja verdadeiro.

O teste de hipóteses para a diferença de duas médias envolve calcular a estatística de teste e compará-la com o valor crítico para rejeitar ou não a hipótese nula. A seguir veremos como realizar um teste de hipótese para a diferença de médias.

Finalmente, lembre-se de que, em estatística, o teste de hipóteses também pode ser chamado de contraste de hipóteses, teste de hipótese ou teste de significância.

➤ Veja: Distribuição amostral de diferença de médias

Fórmula de teste de hipóteses para diferença de médias

A fórmula que deve ser usada para testar hipóteses sobre a diferença de médias varia dependendo se as variâncias populacionais são conhecidas e, se não, se podem ser consideradas iguais ou diferentes. Portanto, nesta seção veremos qual fórmula usar dependendo do caso.

Variações conhecidas

A fórmula para calcular a estatística do teste de hipótese para a diferença de médias quando as variâncias são conhecidas é a seguinte:

$\displaystyle Z=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Ouro:

$Z$

é a estatística de teste de hipótese para a diferença de duas médias com variância conhecida, que segue uma distribuição normal padrão.
$\mu_1$

é a média da população 1.
$\mu_2$

é a média da população 2.
$\overline{x_1}$

é a média da amostra 1.
$\overline{x_2}$

é a média da amostra 2.
$\sigma_1$

é o desvio padrão da população 1.
$\sigma_2$

é o desvio padrão da população 2.
$n_1$

é o tamanho da amostra 1.
$n_2$

é o tamanho da amostra 2.

Lembre-se que este é o caso menos comum, portanto esta fórmula só é utilizada em alguns casos específicos.

Desvios desconhecidos e iguais

A fórmula para calcular a estatística do teste de hipótese para a diferença nas médias quando as variâncias da população são desconhecidas, mas consideradas iguais é:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

Ouro:

$t$

é a estatística de teste de hipótese para a diferença de médias com variâncias desconhecidas, que segue uma distribuição t de Student com n ₁ + n ₂ -2 graus de liberdade.
$\mu_1$

é a média da população 1.
$\mu_2$

é a média da população 2.
$\overline{x_1}$

é a média da amostra 1.
$\overline{x_2}$

é a média da amostra 2.
$s_p$

é o desvio padrão combinado.
$n_1$

é o tamanho da amostra 1.
$n_2$

é o tamanho da amostra 2.

O desvio padrão combinado das duas amostras é calculado com a seguinte fórmula:

$\displaystyle s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

Variações desconhecidas e diferentes

Quando as variâncias populacionais são desconhecidas e, além disso, são assumidas como diferentes, a fórmula para calcular a estatística do teste de hipótese para a diferença de médias é a seguinte:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle \sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$

Ouro:

$t$

é a estatística de teste de hipótese para a diferença de médias com variâncias desconhecidas, que segue a distribuição t de Student.
$\mu_1$

é a média da população 1.
$\mu_2$

é a média da população 2.
$\overline{x_1}$

é a média da amostra 1.
$\overline{x_2}$

é a média da amostra 2.
$\sigma_1$

é o desvio padrão da população 1.
$\sigma_2$

é o desvio padrão da população 2.
$n_1$

é o tamanho da amostra 1.
$n_2$

é o tamanho da amostra 2.

Porém, neste caso, os graus de liberdade da distribuição t de Student são calculados pela seguinte fórmula:

$\displaystyle GL=\frac{\displaystyle\left(\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}\right)^2}{\displaystyle\frac{\displaystyle\frac{s_1^2}{n_1}}{n_1-1}+\frac{\displaystyle\frac{s_2^2}{n_2}}{n_2-1}}$

➤ Veja: Fórmula de intervalo de confiança para diferença de médias

Exemplo concreto de teste de hipótese para a diferença de médias

Para finalizar a assimilação do conceito de teste de hipóteses sobre diferença de médias, veremos um exemplo concreto desse tipo de teste de hipóteses.

Você deseja fazer um estudo estatístico sobre o salário de duas empresas concorrentes, mais especificamente, deseja determinar se o salário médio das duas empresas é diferente. Para isso, são retiradas uma amostra de 47 trabalhadores de uma empresa e outra amostra de 55 trabalhadores da outra empresa. Um salário médio de US$ 40.000 e um desvio padrão de US$ 12.000 são obtidos da primeira amostra, enquanto um salário médio de US$ 46.000 e um desvio padrão de US$ 18.000 são obtidos da segunda amostra. Realize um teste de hipótese com nível de significância de 5% para determinar se os salários médios são diferentes ou não.

Neste caso, a hipótese nula e a hipótese alternativa do teste de hipótese para a diferença das duas médias são as seguintes:

$\begin{cases}H_0: \mu_1-\mu_2=0\\[2ex] H_1:\mu_1-\mu_2\neq 0 \end{cases}$

Neste caso, as disparidades populacionais não são conhecidas, mas pode-se presumir que são iguais porque são empresas concorrentes e as condições de trabalho do mercado em que operam são muito semelhantes. Portanto, a fórmula para a estatística de teste de hipótese para a diferença de médias que devemos usar é:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

Portanto, calculamos o desvio padrão combinado das duas amostras:

$\begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(47-1)\cdot 12000^2+(55-1)\cdot 18000^2}{47+55-2}}\\[2ex]s_p&=15530,61\end{aligned}$

Aplicamos agora a fórmula de teste de hipótese para a diferença de médias:

$\displaystyle t=\frac{\displaystyle (\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}=\cfrac{(40000-46000)-0}{\displaystyle 15530,61\sqrt{\frac{1}{47}+\frac{1}{55}}}=-1,94$

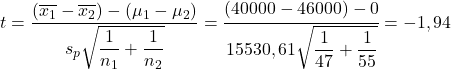
Por outro lado, procuramos o valor crítico do teste de hipótese para a diferença de médias na tabela t de Student :

$\alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 100}=1,984\end{array}$

Então, como o valor absoluto da estatística de teste é menor que o valor crítico do teste, a hipótese nula é aceita e a hipótese alternativa é rejeitada.

$|-1,94|=1,94<1,984 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_1$

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais

O que é teste de hipótese para diferença média?

Fórmula de teste de hipóteses para diferença de médias

Variações conhecidas

Desvios desconhecidos e iguais

Variações desconhecidas e diferentes

Exemplo concreto de teste de hipótese para a diferença de médias

About Author

Dr. benjamim anderson

Add a Comment