Quadrados inferiores

By Dr. benjamim anderson Agosto 2, 2023 Estatisticas 0 Comments

Este artigo explica o que são os mínimos quadrados nas estatísticas, o que é o método dos mínimos quadrados e como um modelo de regressão é ajustado pelo critério dos mínimos quadrados.

Qual é o método dos mínimos quadrados?

O método dos mínimos quadrados é um método estatístico usado para determinar a equação de uma regressão. Ou seja, o método dos mínimos quadrados é um critério utilizado em um modelo de regressão para minimizar o erro obtido no cálculo da equação de regressão.

Concretamente, o método dos mínimos quadrados consiste em minimizar a soma dos quadrados dos resíduos, ou seja, baseia-se na minimização da soma dos quadrados das diferenças entre os valores previstos pelo modelo de regressão e os valores observados . . A seguir veremos em detalhes como um modelo de regressão é ajustado pelo critério dos mínimos quadrados.

A principal característica do método dos mínimos quadrados é que as maiores distâncias entre os valores observados e a função de regressão são minimizadas. Ao contrário de outros critérios de regressão, o método dos mínimos quadrados considera mais importante minimizar resíduos grandes do que resíduos pequenos, uma vez que o quadrado de um número grande é muito maior que o quadrado de um número pequeno. número.

Erro de estimativa

Para compreender completamente o conceito de mínimos quadrados, devemos primeiro ter clareza sobre o que são resíduos em um modelo de regressão. Veremos, portanto, a seguir o que é um erro de estimativa e como ele é calculado.

Em estatística, o erro de estimação , também denominado residual , é a diferença entre o valor verdadeiro e o valor ajustado pelo modelo de regressão. Um resíduo estatístico é, portanto, calculado da seguinte forma:

$e_i=y_i-\widehat{y}_i$

Ouro:

$e_i$

é o resíduo dos dados i.
$y_i$

é o valor real dos dados i.
$\widehat{y}_i$

é o valor fornecido pelo modelo de regressão para os dados i.

Assim, quanto maior o resíduo de um dado, mais mal o modelo de regressão está adaptado a esse dado. Assim, quanto menor for um resíduo, menor será a distância entre o seu valor real e o seu valor previsto.

Da mesma forma, se o resíduo de um dado for positivo, significa que o modelo de regressão prevê um valor inferior ao valor verdadeiro. ao passo que se o resíduo for negativo, significa que o valor previsto é maior que o valor real.

Minimize os quadrados de erro

Agora que sabemos o que é um resíduo nas estatísticas, será mais fácil entender como os quadrados de erro são minimizados.

O quadrado de um erro é o quadrado de um resíduo, portanto o quadrado de um erro é igual à diferença entre o valor verdadeiro e o valor ajustado pelo modelo de regressão elevado à potência de dois.

$e_i^2=(y_i-\widehat{y}_i)^2$

Ouro:

$e_i^2$

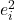
é o quadrado do resíduo dos dados i.
$y_i$

é o valor real dos dados i.
$\widehat{y}_i$

é o valor fornecido pelo modelo de regressão para os dados i.

Assim, o método dos mínimos quadrados consiste em criar um modelo de regressão minimizando a soma dos quadrados dos erros . O critério dos mínimos quadrados baseia-se, portanto, na minimização da seguinte expressão:

$\begin{array}{l} [MIN] \ \displaystyle \sum_{i=1}^ne_i^2\\[4ex][MIN] \ \displaystyle \sum_{i=1}^n(y_i-\widehat{y}_i)^2\end{array}$

É por isso que o critério dos mínimos quadrados também é chamado de critério dos mínimos quadrados.

Como você pode ver na fórmula anterior, o critério dos mínimos quadrados dá mais importância à minimização de resíduos grandes do que a resíduos pequenos. Por exemplo, se um resíduo for 3 e outro resíduo for 5, seus quadrados serão 9 e 25 respectivamente, então o critério dos mínimos quadrados priorizará a minimização do segundo resíduo antes do primeiro resíduo.

Ajuste de mínimos quadrados

Ajustar um modelo de regressão pelo critério dos mínimos quadrados consiste em encontrar um modelo de regressão que minimize os quadrados dos resíduos. Portanto, a equação obtida a partir do modelo de regressão será aquela cujos quadrados das diferenças entre os valores observados e os valores ajustados sejam mínimos.

Observe no exemplo a seguir que existem mais critérios para a criação de um modelo de regressão e, dependendo do critério escolhido, a equação de regressão é diferente.

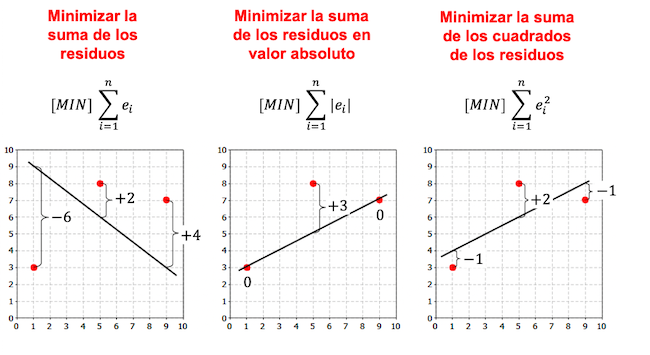
método dos mínimos quadrados, ajuste dos mínimos quadrados

Como você pode ver nos exemplos anteriores, a reta obtida do modelo de regressão linear para o mesmo conjunto de dados depende do critério escolhido. Geralmente, o critério dos mínimos quadrados é usado em modelos de regressão.

Em estatística, o modelo de regressão mais utilizado é o modelo de regressão linear simples, que consiste em aproximar a relação entre a variável independente X e a variável dependente Y por meio de uma linha reta.

$y=b_0+b_1x$

Portanto, as fórmulas para ajustar um conjunto de dados a um modelo de regressão linear simples são:

$b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}$

$b_0=\overline{y}-b_1\overline{x}$

Você pode ver um exemplo de como um modelo de regressão linear simples é calculado usando o critério dos mínimos quadrados clicando no link a seguir:

➤ Veja: Exemplo de regressão linear simples

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais