Regressão logística
Este artigo explica o que é regressão logística em estatísticas. Da mesma forma, você encontrará a fórmula de regressão logística, quais são os diferentes tipos de regressão logística e, além disso, um exercício de regressão logística resolvido.
O que é regressão logística?
Nas estatísticas, a regressão logística é um tipo de modelo de regressão usado para prever o resultado de uma variável categórica . Ou seja, a regressão logística é utilizada para modelar a probabilidade de uma variável categórica assumir um determinado valor com base nas variáveis independentes.
O modelo de regressão logística mais comum é a regressão logística binária, na qual existem apenas dois resultados possíveis: “fracasso” ou “sucesso” ( distribuição de Bernoulli ). “Fracasso” é representado pelo valor 0, enquanto “sucesso” é representado pelo valor 1.
Por exemplo, a probabilidade de um aluno passar em um exame com base nas horas que passou estudando pode ser estudada por meio de um modelo de regressão logística. Neste caso, o fracasso seria o resultado do “fracasso” e, por outro lado, o sucesso seria o resultado do “sucesso”.
Fórmula de regressão logística
A equação para um modelo de regressão logística é:
![]()
Portanto, em um modelo de regressão logística, a probabilidade de se obter o resultado “sucesso”, ou seja, que a variável dependente assuma o valor 1, é calculada com a seguinte fórmula:
![]()
Ouro:
-

é a probabilidade de que a variável dependente seja 1.
-

é a constante do modelo de regressão logística.
-

é o coeficiente de regressão da variável i.
-

é o valor da variável i.
Exemplo de modelo de regressão logística
Agora que conhecemos a definição de regressão logística, vamos ver um exemplo concreto de como criar um modelo desse tipo de regressão.
- Na tabela a seguir, foi compilada uma série de 20 dados que relacionam as horas de estudo de cada aluno e se eles foram aprovados ou reprovados em um exame de estatística. Execute um modelo de regressão logística e calcule a probabilidade de um aluno ser aprovado se estudar 4 horas.
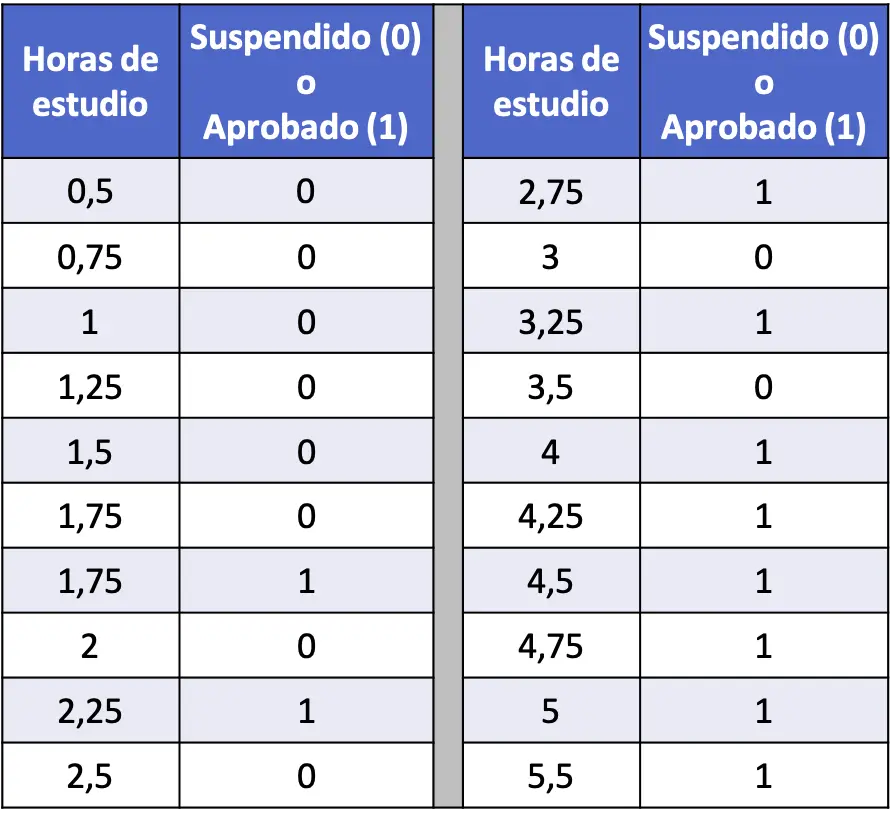
Nesse caso, a variável explicativa é o número de horas de estudo e a variável resposta é se o aluno foi reprovado (0) ou aprovado (1). Portanto, em nosso modelo teremos apenas o coeficiente
![]()
e o coeficiente
![]()
, uma vez que existe apenas uma variável independente.
![]()
A determinação manual dos coeficientes de regressão é muito trabalhosa, por isso é recomendado o uso de software de computador como o Minitab. Assim, os valores dos coeficientes de regressão calculados utilizando o Minitab são os seguintes:
![Rendered by QuickLaTeX.com \begin{array}{c}\beta_0\approx -4,1\\[2ex]\beta_1\approx 1,5\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-6ed66de602220c69aabb71a726fec9f8_l3.png)
O modelo de regressão logística é, portanto, o seguinte:
![Rendered by QuickLaTeX.com \begin{aligned}p&=\cfrac{1}{1+e^{-(\beta_0+\beta_1x_1+\beta_2x_2+\dots+\beta_ix_i)}}\\[2ex]p&=\cfrac{1}{1+e^{-(-4,1+1,5x_1)}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0902ac67194bedf38d5f4ff06dc27a38_l3.png)
Abaixo você pode ver os dados de amostra e a equação do modelo de regressão logística representada graficamente:
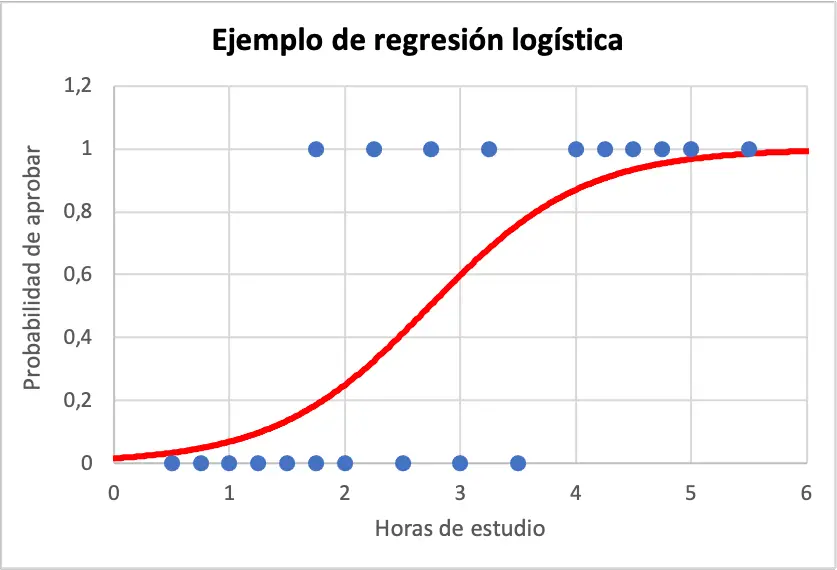
Assim, para calcular a probabilidade de um aluno ter sucesso caso tenha estudado 4 horas, basta utilizar a equação obtida no modelo de regressão logística:
![Rendered by QuickLaTeX.com \begin{aligned}p&=\cfrac{1}{1+e^{4,1-1,5x_1}}\\[2ex]p&=\cfrac{1}{1+e^{4,1-1,5\cdot 4}}\\[2ex]p&=0,8699\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-930691eafee62c04e59d9c4de8ef6a76_l3.png)
Resumindo, se um aluno estudar quatro horas terá 86,99% de probabilidade de passar no exame.
Tipos de regressão logística
Existem três tipos de regressão logística :
- Regressão Logística Binária : A variável dependente só pode ter dois valores (0 e 1).
- Regressão logística multinomial : A variável dependente possui mais de dois valores possíveis.
- Regressão logística ordinal : os resultados possíveis têm uma ordem natural.
Regressão logística e regressão linear
Por fim, de forma resumida, veremos qual a diferença entre uma regressão logística e uma regressão linear, já que o modelo de regressão mais utilizado em estatística é o modelo linear.
A regressão linear é usada para modelar variáveis dependentes numéricas. Além disso, na regressão linear, a relação entre as variáveis explicativas e a variável resposta é linear.
Portanto, a principal diferença entre regressão logística e regressão linear é o tipo de variável dependente. Numa regressão logística, a variável dependente é categórica, enquanto a variável dependente numa regressão linear é numérica.
Assim, a regressão logística é usada para prever um resultado entre duas opções possíveis, enquanto a regressão linear ajuda a prever um resultado numérico.