Linha de regressão
Este artigo explica o que é linha de regressão nas estatísticas. Assim, você encontrará como calcular a reta de regressão entre duas variáveis, um exercício resolvido e, além disso, uma calculadora online para calcular a reta de regressão para qualquer amostra de dados.
Qual é a linha de regressão?
Em estatística, a reta de regressão é a reta obtida a partir de um modelo de regressão linear simples . Mais precisamente, a linha de regressão é a linha que melhor se ajusta a um gráfico de dispersão e, portanto, descreve melhor um conjunto de dados estatísticos.
Assim, a equação da linha de regressão relaciona matematicamente a variável independente X e a variável dependente Y de um conjunto de dados. Embora a linha de regressão geralmente não seja capaz de determinar com precisão o valor de cada observação, ela pode fornecer uma aproximação do seu valor.

Como você pode ver no gráfico anterior, a linha de regressão nos ajuda a ver a tendência de um conjunto de dados e que tipo de relacionamento existe entre a variável independente e a variável dependente. Abaixo veremos as aplicações da linha de regressão.
Fórmula da linha de regressão
Agora que sabemos a definição da reta de regressão, vamos ver como calcular a equação da reta de um modelo de regressão linear.
Como qualquer reta, a equação da reta de regressão é composta por uma constante (b 0 ) e uma inclinação (b 1 ):
![]()
Assim, as fórmulas para cálculo dos coeficientes da reta de regressão linear são as seguintes:
![Rendered by QuickLaTeX.com \begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[12ex]b_0=\overline{y}-b_1\overline{x}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-6dc6f56cacf0a233977c358d6a62fca8_l3.png)
Ouro:
-
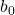
é a constante da linha de regressão.
-
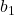
é a inclinação da linha de regressão.
-

é o valor da variável independente X dos dados i.
-

é o valor da variável dependente Y dos dados i.
-

é a média dos valores da variável independente
-

é a média dos valores da variável dependente Y.
👉 Você pode usar a calculadora abaixo para calcular a linha de regressão para qualquer conjunto de dados.
Exemplo concreto da linha de regressão
Para explorar mais o conceito de linha de regressão, abaixo está um exemplo prático de como criar uma linha de regressão.
- Após a realização de uma prova de estatística, cinco alunos foram questionados sobre quantas horas de estudo dedicaram à prova, os dados estão apresentados na tabela abaixo. Calcule a reta de regressão a partir dos dados estatísticos coletados para relacionar linearmente as horas de estudo com a nota obtida. A seguir, determine qual será a nota obtida por um aluno que estudou 8 horas.

Para encontrar a reta de regressão dos dados amostrais, precisamos determinar os coeficientes b 0 e b 1 da equação e, para isso, precisamos utilizar as fórmulas vistas na seção acima.
Porém, para aplicar as fórmulas da reta de regressão linear, devemos primeiro calcular a média da variável independente e a média da variável dependente:
![Rendered by QuickLaTeX.com \begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7a7aa6f1f20fa4ff0d61a2ad0dd2ea1f_l3.png)
Agora que conhecemos as médias das variáveis, calculamos o coeficiente b 1 do modelo utilizando sua fórmula correspondente:
![Rendered by QuickLaTeX.com \begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c9d90c766487cd7b6924e6b23d2d9c78_l3.png)
Por fim, calculamos o coeficiente b 0 do modelo utilizando sua fórmula correspondente:
![Rendered by QuickLaTeX.com \begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c72e6b89a75681a88cf751ca39079240_l3.png)
Resumindo, a equação da reta de regressão linear do problema é a seguinte:
![]()
Abaixo você pode ver a representação gráfica dos dados amostrais, bem como a reta do modelo de regressão linear simples:

Uma vez calculada a reta de regressão, para prever a nota que obterá um aluno que estudou 8 horas, basta substituir este valor na equação da reta de regressão obtida:
![]()
Assim, de acordo com o modelo de regressão linear realizado, se um aluno estudou oito horas, obterá nota 5,56 no exame.
Para que serve uma linha de regressão?
Principalmente, a linha de regressão tem duas utilizações: a linha de regressão é usada para determinar que tipo de relação existe entre duas variáveis e, por outro lado, a linha de regressão também permite fazer uma previsão sobre o valor de uma nova observação.
A inclinação da linha de regressão nos diz como é a correlação entre a variável independente e a variável dependente. Se a inclinação for positiva, significa que a variável dependente é diretamente proporcional à variável independente, enquanto se a inclinação for negativa, implica que as variáveis são inversamente proporcionais. Finalmente, se o coeficiente de inclinação estiver muito próximo de zero, isso significa que a correlação entre as duas variáveis é muito fraca.
Além disso, se a equação da reta de regressão for conhecida, o valor da variável dependente pode ser previsto para um novo valor da variável independente, como fizemos no exemplo acima. Assim, quanto melhor a linha de regressão for adaptada, melhores serão as previsões que ela fará.
Calculadora de linha de regressão
Insira uma amostra de dados na calculadora a seguir para calcular a linha de regressão entre as duas variáveis. É necessário separar os pares de dados, para que na primeira caixa existam apenas os valores da variável independente X e na segunda caixa existam apenas os valores da variável dependente Y.
Os dados devem ser separados por espaço e inseridos usando o ponto final como separador decimal.