Qualidade de ajuste
Este artigo explica o que é a qualidade do ajuste nas estatísticas. Da mesma forma, mostra como medir a qualidade do ajuste de um modelo de regressão e, além disso, você poderá ver um exercício resolvido de qualidade do ajuste.
O que é qualidade de ajuste?
Nas estatísticas, a qualidade do ajuste é o quão bem um modelo de regressão se ajusta à amostra de dados. Em outras palavras, a qualidade do ajuste de um modelo de regressão refere-se ao nível de acoplamento entre o conjunto de observações e os valores obtidos através da regressão.
Portanto, quanto melhor for o ajuste de um modelo de regressão, melhor ele explica os dados que estão sendo estudados. Assim, queremos que quanto melhor ajuste do modelo estatístico, melhor.
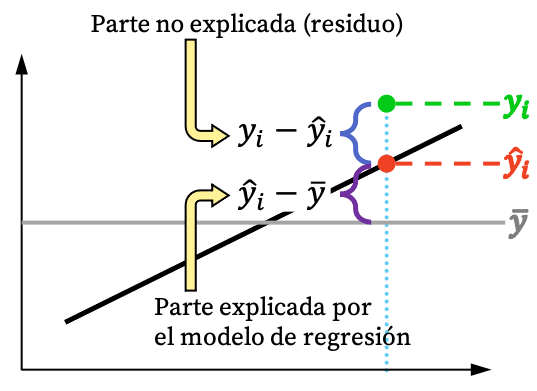
Como você pode ver na imagem acima, o valor de uma observação geralmente não pode ser totalmente explicado pelo modelo de regressão. Mas logicamente, quanto mais o modelo de regressão puder explicar a partir do conjunto de dados, melhor será o ajuste do modelo. Em suma, estamos interessados num modelo de regressão que seja o mais rigoroso possível.
Qualidade de ajuste de um modelo de regressão
Para determinar a qualidade do ajuste de um modelo de regressão, normalmente utiliza-se o coeficiente de determinação , que é um coeficiente estatístico que indica a porcentagem explicada pelo modelo de regressão. Assim, quanto maior o coeficiente de determinação de um modelo, melhor o modelo se adaptará à amostra de dados.
![]()
Contudo, deve-se notar que quanto mais variáveis um modelo de regressão tiver, maior será o seu coeficiente de determinação. Por esta razão, o coeficiente de determinação ajustado também é frequentemente usado para medir a qualidade do ajuste de um modelo. O coeficiente de determinação ajustado é uma variação do coeficiente anterior que indica o percentual explicado pelo modelo de regressão, penalizando para cada variável explicativa incluída no modelo.
![]()
É portanto preferível utilizar o coeficiente de determinação ajustado para comparar dois modelos com um número de variáveis diferentes, porque tem em conta o número de variáveis incluídas no modelo.
Por fim, deve-se notar que o teste Qui-quadrado também pode ser utilizado para medir a qualidade do ajuste de um modelo de regressão, embora normalmente sejam utilizados os valores dos dois coeficientes anteriores.
Exemplo concreto de bom ajuste
Por fim, veremos um exercício resolvido de qualidade de ajuste para finalizar a assimilação deste conceito estatístico.
- Com a mesma série de dados, são realizados dois modelos de regressão linear diferentes, cujos resultados você pode ver na tabela a seguir. Qual modelo é melhor usar?
| Modelo de regressão 1 | Modelo de regressão 2 | |
|---|---|---|
| Coeficiente de determinação | 57% | 64% |
| Coeficiente de determinação ajustado | 49% | 43% |
| Número de variáveis explicativas | 3 | 7 |
Neste caso, assumimos que ambos os modelos satisfazem os pressupostos anteriores dos modelos de regressão linear e, portanto, precisamos apenas analisar a qualidade do ajuste dos modelos.
O modelo de regressão 2 tem um coeficiente de determinação mais elevado do que o modelo de regressão 1, pelo que parece a priori ser um modelo de regressão melhor, uma vez que é capaz de explicar melhor a amostra de dados.
No entanto, o Modelo de Regressão 2 possui 7 variáveis independentes no modelo, enquanto o Modelo de Regressão 1 possui apenas 3. Portanto, o Modelo 2 será muito mais complicado e mais difícil de interpretar do que o primeiro modelo.
Além disso, se observarmos o coeficiente de determinação ajustado, que leva em consideração o número de variáveis do modelo, o modelo de regressão 1 apresenta um coeficiente de determinação ajustado maior que o modelo de regressão 2.
Concluindo, embora seja melhor utilizar o modelo de regressão 1, pois seu coeficiente de determinação ajustado é superior ao do modelo de regressão 2. o modelo de regressão 2 tem um coeficiente de determinação não ajustado maior, é porque incluíram muito mais variáveis na regressão modelo 1. modelo, que aumenta o valor do referido coeficiente, mas dificulta a interpretação do modelo e, certamente, piora a previsão de um novo valor.
Para comparar modelos com diferentes números de variáveis, é melhor utilizar o coeficiente de determinação ajustado porque ele penaliza cada variável adicionada ao modelo. Como você viu neste exemplo, de acordo com o coeficiente de determinação não ajustado, o modelo de regressão 2 é melhor, porém, através do coeficiente de determinação ajustado podemos saber que o modelo de regressão 1 é realmente melhor.