Como realizar a regressão loess em r (com exemplo)

A regressão LOESS , às vezes chamada de regressão local, é um método que usa ajuste local para ajustar um modelo de regressão a um conjunto de dados.

O exemplo passo a passo a seguir mostra como realizar a regressão LOESS em R.

Etapa 1: crie os dados

Primeiro, vamos criar o seguinte quadro de dados em R:

 #view DataFrame
df <- data. frame (x=c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14),
                 y=c(1, 4, 7, 13, 19, 24, 20, 15, 13, 11, 15, 18, 22, 27))

#view first six rows of data frame
head(df)

  xy
1 1 1
2 2 4
3 3 7
4 4 13
5 5 19
6 6 24

Etapa 2: Ajustar vários modelos de regressão LOESS

Podemos usar a função loess() para ajustar vários modelos de regressão LOESS a este conjunto de dados, usando valores diferentes para o parâmetro span :

 #fit several LOESS regression models to dataset
loess50 <- loess(y ~ x, data=df, span= .5 )
smooth50 <- predict(loess50) 

loess75 <- loess(y ~ x, data=df, span= .75 )
smooth75 <- predict(loess75) 

loess90 <- loess(y ~ x, data=df, span= .9 )
smooth90 <- predict(loess90) 

#create scatterplot with each regression line overlaid
plot(df$x, df$y, pch= 19 , main=' Loess Regression Models ')
lines(smooth50, x=df$x, col=' red ')
lines(smooth75, x=df$x, col=' purple ')
lines(smooth90, x=df$x, col=' blue ')
legend(' bottomright ', legend=c(' .5 ', ' .75 ', ' .9 '),
        col=c(' red ', ' purple ', ' blue '), pch= 19 , title=' Smoothing Span ')

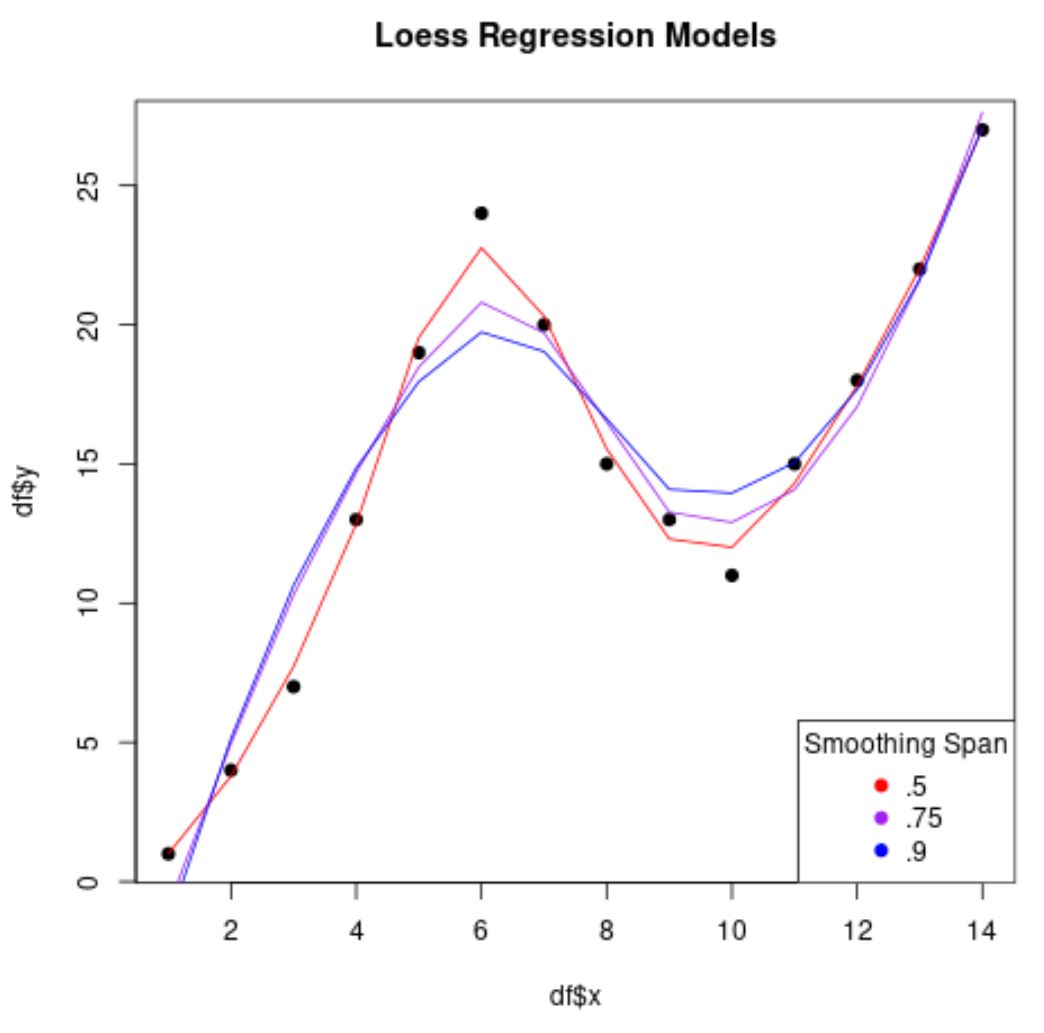
Observe que quanto menor o valor que usamos para span , menos “suave” será o modelo de regressão e mais o modelo tentará ajustar os pontos de dados.

Etapa 3: use a validação cruzada K-Fold para encontrar o melhor modelo

Para encontrar o valor de extensão ideal a ser usado, podemos realizar validação cruzada k-fold usando funções no pacote circunflexo :

 library (caret)

#define k-fold cross validation method
ctrl <- trainControl(method = " cv ", number = 5 )
grid <- expand. grid (span = seq( 0.5 , 0.9 , len = 5 ), degree = 1 )

#perform cross-validation using smoothing spans ranging from 0.5 to 0.9
model <- train(y ~ x, data = df, method = " gamLoess ", tuneGrid=grid, trControl = ctrl)

#print results of k-fold cross-validation
print (model)

14 samples
 1 predictor

No pre-processing
Resampling: Cross-Validated (5 fold) 
Summary of sample sizes: 12, 11, 11, 11, 11 
Resampling results across tuning parameters:

  span RMSE Rsquared MAE      
  0.5 10.148315 0.9570137 6.467066
  0.6 7.854113 0.9350278 5.343473
  0.7 6.113610 0.8150066 4.769545
  0.8 17.814105 0.8202561 11.875943
  0.9 26.705626 0.7384931 17.304833

Tuning parameter 'degree' was held constant at a value of 1
RMSE was used to select the optimal model using the smallest value.
The final values used for the model were span = 0.7 and degree = 1.

Podemos ver que o valor de amplitude que produziu o valor mais baixo para a raiz do erro quadrático médio (RMSE) é 0,7 .

Portanto, para nosso modelo de regressão LOESS final, escolheríamos usar um valor de 0,7 para o argumento span na função loess() .

Recursos adicionais

Os tutoriais a seguir fornecem informações adicionais sobre modelos de regressão em R:

Como realizar regressão linear simples em R
Como realizar regressão linear múltipla em R
Como realizar regressão logística em R
Como realizar regressão quantílica em R
Como realizar regressão ponderada em R