Limites de controle

By Dr. benjamim anderson Agosto 2, 2023 Gestão da qualidade 0 Comments

Este artigo explica o que é um limite de controle e quais são os diferentes limites de controle de um gráfico de controle. Você também verá como os limites de controle são calculados, bem como um exemplo prático no qual os limites de controle de um processo são determinados.

Quais são os limites de controle?

Os limites de controle são as linhas horizontais em um gráfico de controle usadas para determinar se um processo é controlado ou não.

Um gráfico de controle possui dois limites de controle: os limites de controle superior e inferior, que demarcam a área de controle acima e abaixo, respectivamente.

Então, limites de controle são valores utilizados para indicar a área de controle de um processo. Se a medição obtida de um processo estiver dentro dos limites de controle, significa que o processo está controlado. Caso contrário, a máquina ou processo deve ser verificado porque é provável que tenha se desviado.

Tipos de limites de controle

Os limites de controle são:

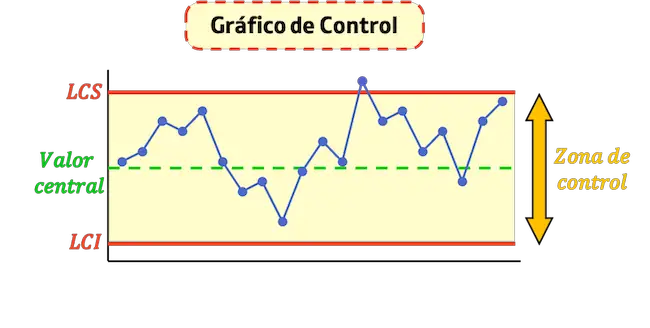
Limite Superior de Controle (LCS) : é a linha que indica o valor máximo aceito no processo.
Limite Inferior de Controle (LCI) : É a linha que indica o valor mínimo aceito no processo.
Linha de controle central : Esta é a linha que representa o valor médio do gráfico. Quanto mais próximos os pontos estiverem desta linha, mais estável será o processo.

Como calcular limites de controle

Atualmente, os limites de controle de um processo são geralmente calculados por softwares de computador que permitem controlar o processo. Porém, também é importante que você saiba como eles são calculados, pois pode ser necessário localizá-los manualmente.

O cálculo dos limites de controle de um gráfico de controle depende do tipo de gráfico que você deseja fazer, pois os valores mudarão dependendo se é um gráfico de controle para média ou para faixa.

O gráfico de controle médio é um gráfico no qual é avaliada a evolução da média de um processo. Assim, a média de um conjunto de valores é calculada pela seguinte fórmula:

$\overline{X}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}$

Ouro:

$x_i$

é o número da medida i.
$n$

é o número de medições realizadas.

Designaremos o valor central do gráfico de controle para a média como

$\overline{\overline{X}}$

, que é a média das amostras e é calculada com a seguinte expressão:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}$

Ouro:

$\overline{X}_j$

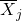
é a média da amostra j.
$m$

é o número de amostras colhidas.

➤ Veja: Cálculo da média aritmética

Em contraste, o valor central do gráfico de controle de extensão é a média das extensões de todas as amostras colhidas:

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}$

Ouro:

$R_j$

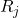
é o intervalo da amostra j.
$m$

é o número de amostras colhidas.

➤ Veja: Cálculo do intervalo estatístico

Assim, as fórmulas para cálculo dos limites de controle de um gráfico de controle são as seguintes:

cartão de controle

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}\end{array}$

Cartão de controle R

$\begin{array}{c}LCS=D_4\cdot \overline{R}\\[3ex]LCI=D_3\cdot\overline{R}\end{array}$

Onde os valores dos parâmetros A ₂ , D ₃ e D ₄ se encontram na tabela a seguir:

Tamanho (não.)	Às ₂	Dia ₃	_J4
2	1.880	0,000	3.267
3	1.023	0,000	2.575
4	0,729	0,000	2.282
5	0,577	0,000	2.115
6	0,483	0,000	2004
7	0,419	0,076	1.924
8	0,373	0,136	1.864
9	0,337	0,184	1.816
dez	0,308	0,223	1.777

Exemplo de cálculo de limites de controle

Uma empresa industrial deseja controlar a medição do diâmetro de um cilindro para verificar se seu processo produtivo está sob controle. Para fazer isso, pegue uma amostra de 5 cilindros a cada 15 minutos e meça seu diâmetro. A tabela a seguir mostra o registro da medição.

Para encontrar os limites de controle, devemos primeiro tomar a média aritmética e o intervalo de cada conjunto de medidas:

exemplos de cálculos de gráfico de controle

Agora vamos calcular a média das médias e dos intervalos, que serão os valores centrais do gráfico de controle para a média e para o intervalo, respectivamente:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}=4,8589$

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}=0,0227$

Neste caso, cada amostra é composta por 5 medições, os coeficientes das fórmulas do limite de controle são, portanto, os seguintes:

$A_2=0,577$

$D_3=0$

$D_4=2,115$

Calculamos os limites de controle superior e inferior do gráfico de controle médio e estendido:

Limites de controle do gráfico de controle

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}=4,8589+0,577\cdot 0,0227=4,8720\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}=4,8589-0,577\cdot 0,0227=4,8458\end{array}$

Limites de controle de Cartão de controle R

$\begin{array}{c}LCS=D_4\cdot \overline{R}=2,115\cdot 0,0227=0,0481\\[3ex]LCI=D_3\cdot\overline{R}=0\cdot 0,0227=0\end{array}$

Os cartões de controle de exercício são, portanto, os seguintes:

exemplo de cálculo de limites de controle

No primeiro gráfico de controle podemos ver que dois valores são menores que o limite inferior de controle. Adicionalmente, no segundo gráfico de controle, também existe um valor acima do limite superior de controle. O processo, portanto, não é controlado.

About Author

Dr. benjamim anderson

Olá, sou Benjamin, um professor aposentado de estatística que se tornou professor dedicado na Statorials. Com vasta experiência e conhecimento na área de estatística, estou empenhado em compartilhar meu conhecimento para capacitar os alunos por meio de Statorials. Saber mais

Quais são os limites de controle?

Tipos de limites de controle

Como calcular limites de controle

Exemplo de cálculo de limites de controle

About Author

Dr. benjamim anderson

Add a Comment