Como calcular quartis para dados agrupados
Quartis são valores que dividem um conjunto de dados em quatro partes iguais.
Você pode usar a seguinte fórmula para calcular quartis para dados agrupados:
Q i = L + (C/F) * (iN/4 – M)
Ouro:
- L : O limite inferior do intervalo que contém o i- ésimo quartil
- C : A largura da classe
- F : A frequência do intervalo que contém o i- ésimo quartil
- N : A frequência total
- M : A frequência cumulativa que leva ao intervalo que contém o i- ésimo quartil
O exemplo a seguir mostra como usar esta fórmula na prática.
Exemplo: Calcular quartis para dados agrupados
Suponha que temos a seguinte distribuição de frequência:
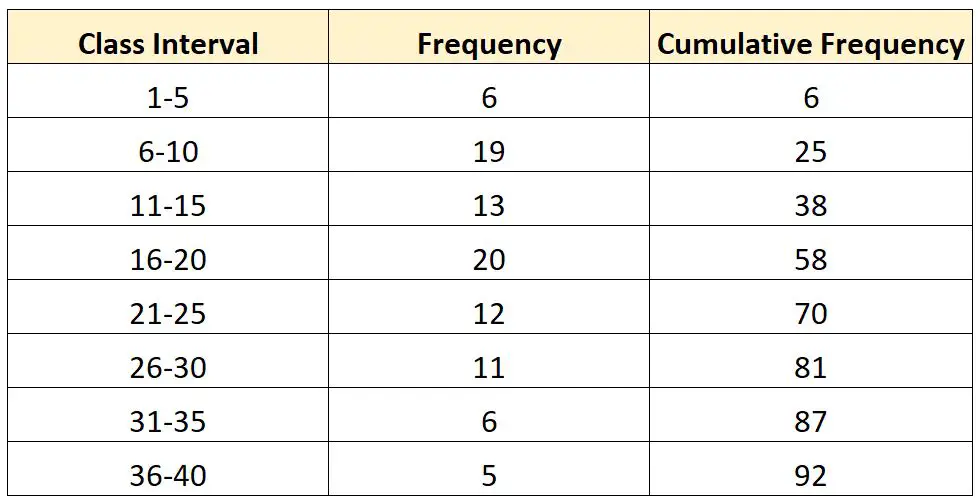
Agora suponhamos que queremos calcular o valor no terceiro quartil (Q 3 ) desta distribuição.
O valor do terceiro quartil estará localizado na posição (iN/4) da distribuição.
Então, (iN/4) = (3*92/4) = 69.
O intervalo que contém o terceiro quartil será o intervalo 21-25 , uma vez que 69 está entre as frequências cumulativas de 58 e 70.
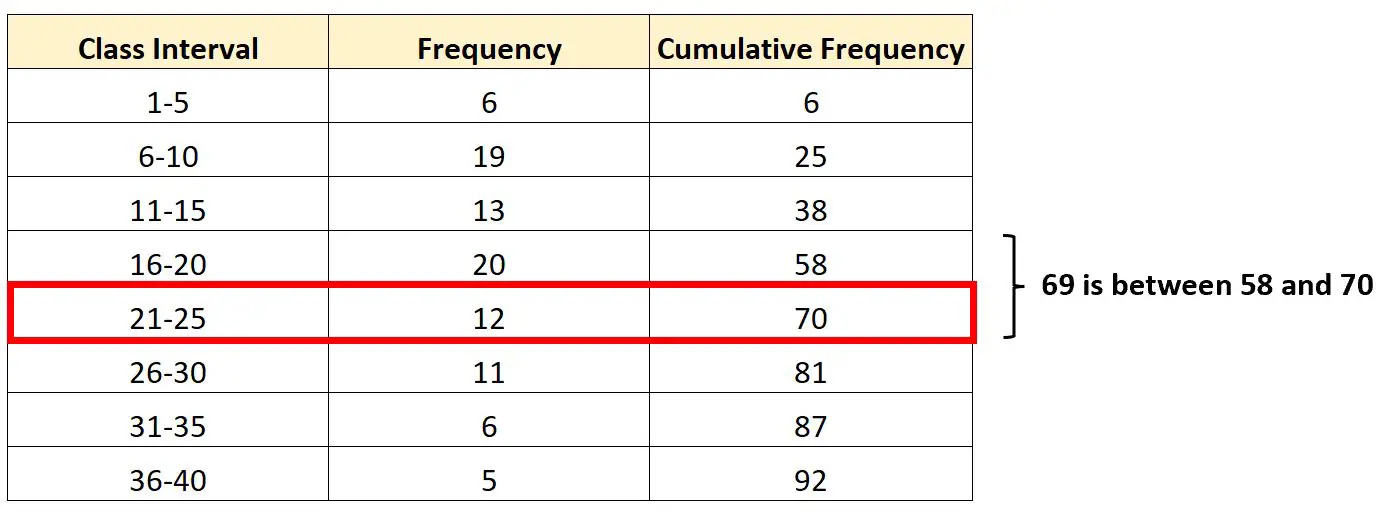
Sabendo disso, podemos encontrar cada um dos valores necessários para inserir em nossa fórmula:
L : O limite inferior do intervalo que contém o i- ésimo quartil
- O limite inferior do intervalo é 21 .
C : A largura da classe
- A largura da classe é calculada da seguinte forma: 25 – 21 = 4 .
F : A frequência do intervalo que contém o i- ésimo quartil
- A frequência da aula 21-25 é 12
N : A frequência total
- A frequência cumulativa total na tabela é 92 .
M : A frequência cumulativa que leva ao intervalo que contém o i- ésimo quartil
- A frequência acumulada até às classes 21-25 é de 58 .
Podemos então inserir todos esses valores na fórmula anterior para encontrar o valor no terceiro quartil:
- Q i = L + (C/F) * (iN/4 – M)
- Q3 = 21 + (4/12) * ((3)(92)/4 – 58)
- Q3 = 24,67
O valor no terceiro quartil é 24,67 .
Você pode usar uma abordagem semelhante para calcular os valores do primeiro e do segundo quartil.
Recursos adicionais
Os tutoriais a seguir fornecem informações adicionais sobre como trabalhar com dados agrupados:
Como encontrar a média e o desvio padrão de dados agrupados
Como encontrar o modo de dados agrupados
Como encontrar a mediana de dados agrupados
Distribuições de frequência agrupadas ou desagrupadas